Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 11-02-2015 17:38:17
- Maumo97x
- Membre
- Inscription : 11-02-2015
- Messages : 1
En lien avec l'architecture (Fonction polynôme de degré 2 )
BONJOUR / BONSOIR
alors j'aurais besoin d'un peu d'aide pour cette exercice svp. Tout en sachant que je ne comprends rien au Fonction polynôme de degré 2 ) :
Le viaduc ferroviaire de Garabit est soutenu par une arche parabolique. Les piles sur lesquelles l'arche est posée sont distantes de 165 m, et le sommet de l'arche est situé 57 m plus haut que chacune des piles. On veut calculer la hauteur séparant l'arche du rail au niveau des deux piliers métalliques intermédiaires, situés à 49 m et 116 m de l'entrée de gauche du pont, à l'aplomb de la pile. Pour cela, on modélise la situation à l'aide d'une parabole admettent la courbe représentative ci-dessus ( ci-joint les photo). On appelle [tex]f[/tex] la fonction définie sur l'intervalle I = [0 ; 165] qui admet cette courbe pour représentation graphique.
1. Justifier que pour tout réel [tex]x \in I[/tex], on a :
[tex]f(x)=a(x-82,5)^2+57[/tex] où [tex]a[/tex] est un réel fixé.
2. Quel est le signe de [tex]a[/tex] ? Justifier que [tex]a = -0.0084[/tex].
3. En déduire l'image [tex]f(49)[/tex], puis conclure.
Merci d'avance
Dernière modification par yoshi (11-02-2015 17:57:05)
Hors ligne
#2 11-02-2015 18:04:06
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonjour,
Bienvenue à bord...
( ci-joint les photo)
Bin non, y en a pas...
Pour afficher une image :
1. Il faut la transférer (upload) depuis ton disque dur chez un hébergeur d'image gratuit : casimage.com, hostingspics.net,Photobucket, imageshack.us... etc
3. Cela fait, on te donnera un lien
3. Copier le lien pour les forums (grand format)
4. Le coller dans ton post.
Pour une image d'un dessin d'accord !
Poster l'image d'un texte, sauf cas particulier, Non ! Recopier ce texte ou utiliser la fonction OCR (Reconnaissance de caractères) de votre scanner d'autant qu'en général les imprimantes maintenant sont multifonctions et ont donc un scanner intégré.
Poster une photo d'un dessin, ça le fait pas non plus, mieux vaut passer là encore par un scanner. A défaut, retraiter la photo pour qu'elle soit lisible, de préférence en N&B (niveaux de gris, en fait)...
C'est ça ?
@+
[EDIT] Je ne vais pas avoir le temps de répondre avant Vendredi. Si quelqu'un veut s'y coller...
Bon je fais un effort quand même...
Tout en sachant que je ne comprends rien aux fonctions polynôme de degré 2 ) :
Mouais ! Un peu facile comme alibi quand même...
Pt'êt que commencer par savoir tes leçons t'aiderait un peu...
Bon, la forme développée générale d'une fonction polynôme du 2nd degré est [tex]f(x) = ax^2+bx+c[/tex] où a, b et c sont des réels donnés.
Mais la leçon dit aussi qu'on peut écrire ce polynôme sous "forme canonique" : [tex]a(x-\alpha)^2+\beta[/tex] où [tex](\alpha\;;\;\beta)[/tex] sont les coordonnées du sommet et a un réel donné.
On y arrive comme ceci :
[tex]ax^2+bx+c = a\left(x^2+\frac b a x+\frac c a\right)= a\left[\left(x^2+\frac b a x\right)+\frac c a\right]= a\left[\left(x+\frac{b}{2a}\right)^2 -\frac{b^2}{4a^2}+\frac c a\right] [/tex]
D'où :
[tex]ax^2+bx+c = a\left[\left(x+\frac{b}{2a}\right)^2 -\frac{b^2-4ac}{4a^2}\right]=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}=a\left(x-\left(-\frac{b}{2a}\right)\right)^2+\frac{-b^2+4ac}{4a}[/tex]
Les coordonnées du sommet d'une parabole (cf cours) étant [tex](\alpha\;;\;\beta)[/tex] avec [tex]\alpha =-\frac{b}{2a}[/tex] et [tex]\beta =f\left(-\frac{b}{2a}\right)= \frac{-b^2+4ac}{4a}[/tex]
La fonction s'écrit donc bien : [tex]f(x)=a(x-\alpha)^2+\beta[/tex]
C'est l'essentiel à savoir, les calculs pour l'obtenir, c'est "la cerise sur le gâteau"...
On t'a forcément donné un système d'axes orthonormé dont l'origine est la base du pilier de gauche, moyennant quoi ces coordonnées [tex](\alpha\;;\;\beta)[/tex] sont à déduire de l'énoncé par simple lecture (le sommet de la courbe est pile au milieu entre les deux piliers)...
Voilà pour la Q1
Q2 Selon que la courbe est de cette forme [tex]\cup[/tex] ou celle-ci [tex]\cap[/tex], le signe de a est + ou - : voir ton cours.
Pour trouver a, tu sais que [tex]f(0) = 0[/tex], donc...
Q3 C'est juste du calcul "bête" et (même pas méchant), t'as qu'à demander à ta calculette, il y en a pour une min à taper le calcul !
Reviens nous dire si tu as tout compris ou ce que tu n'as pas compris sachant qu'il te faudra dans ce dernier cas expliquer ce que tu n'as compris où ça bloque et pourquoi...
Extrait de nos Règles :
* Notre but étant de vous aider à résoudre vos difficultés, et non de faire les exercices à votre place, ne postez pas le sujet d'un exercice sans montrer que vous y avez travaillé : il n'y serait probablement pas répondu. A vous d'expliquer ce que vous avez déjà fait, là où vous bloquez, et pourquoi...
Donc, au boulot, sachant que je me suis montré très compréhensif, mais que je ne peux pas faire plus, sans faire le boulot à ta place, ce qui ne sera pas... ;-D
Là je me retire de la circulation...
@+
Dernière modification par yoshi (11-02-2015 20:19:43)
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 13-02-2015 12:42:33
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Re,
Le viaduc de Garabit est l'œuvre de Gustave Eiffel...
En voici une image simplifiée :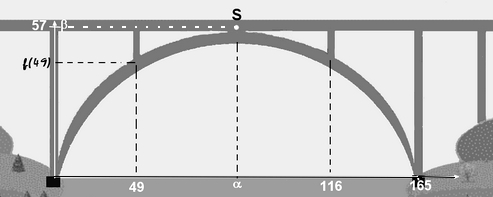
Pour les lecteurs ou Maumo97x si jamais il repassait par là :
[tex]ax^2+bx+c = a\left(x^2+\frac b a x+\frac c a\right)= a\left[\left(x^2+\frac b a x\right)+\frac c a\right][/tex]
On met a en facteur, puis j'isole (cette étape n'est pas indispensable) dans la même parenthèse les deux premiers termes...
On considère alors ces deux premiers termes comme le débit du développement de [tex]\left(x+\frac{b}{2a}\right)^2[/tex] :
[tex]\left(x+\frac{b}{2a}\right)^2 = x^2+\frac b a x +\frac{b^2}{4a^2}[/tex]
On en tire [tex]x^2+\frac b a x = \left(x+\frac{b}{2a}\right)^2 -\frac{b^2}{4a^2}[/tex]
que je remplace :
[tex]ax^2+bx+c = a\left[\left(x^2+\frac b a x\right)+\frac c a\right]= a\left[\left(x+\frac{b}{2a}\right)^2 -\frac{b^2}{4a^2}+\frac c a\right] [/tex]
Et je regroupe les[tex]ax^2+bx+c = a\left[\left(x+\frac{b}{2a}\right)^2 -\frac{b^2}{4a^2}+\frac c a\right] [/tex] deux derniers termes sur une même fraction :
Je vais faire apparaître [tex]-\frac{b}{2a}\; (= \alpha)[/tex] et [tex]\frac{-b^2+4ac}{4a}\; ( =\beta)[/tex] :
[tex]\frac{b}{2a} =-\left(-\frac{b}{2a}\right) \;\;(=-\alpha)[/tex]
et
[tex]-\frac{b^2-4ac}{4a^2}=+\frac{-b^2+4ac}{4a^2}\;\;(=+\frac{\beta}{a})[/tex]
Je remplace et je fais apparaître [tex]-\frac{b}{2a}[/tex] et [tex]-b^2+4ac[/tex] :
[tex]a\left[\left(x+\frac{b}{2a}\right)^2 -\frac{b^2-4ac}{4a^2}\right]= a\left[\left(x-\left(-\frac{b}{2a}\right)\right)^2 +\frac{-b^2+4ac}{4a^2}\right][/tex]
puis je distribue le a qui modifie le 2e dénominateur et fait apparaître [tex]\beta[/tex] seul, donc :
[tex]ax^2+bx+c=a\left[x-\left(-\frac{b}{2a}\right)\right]^2 +\frac{-b^2+4ac}{4a}=a(x-\alpha)^2+\beta[/tex]
Là on reconnaît la forme attendue par l''énoncé : [tex]f(x)=a(x-82,5)^2+57[/tex]
Et donc, aucun calcul à faire (enfin, si, obtenir 82,5 à partir de 165...).
J'ai ajouté sur le dessin [tex]f(49)[/tex] pour bien montrer que ce n'est pas encore la réponse attendue.
Maintenant, il ne manque plus que la visite de Maumo97x...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#4 16-02-2015 09:26:19
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Re,
Encore un consommateur qui a considéré qu'on était tenu de lui répondre, mais lui pas tenu de donner signe de vie...
Décevant !
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 22-02-2015 11:01:38
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonjour,
11 jours plus tard, notre ami se réveille et reposte le même sujet : http://www.bibmath.net/forums/viewtopic … 591#p50591.
Je résume :
Bon, la forme développée générale d'une fonction polynôme du 2nd degré est [tex]f(x)=ax^2+bx+c[/tex] où a, b et c sont des réels donnés.
Mais la leçon dit aussi qu'on peut écrire ce polynôme sous "forme canonique" : [tex]a(x−\alpha)^2+\beta[/tex] où (α;β) sont les coordonnées du sommet et a un réel donné.
Je compare : [tex]f(x)=a(x−\alpha)^2+\beta[/tex] où (α;β) sont les coordonnées du sommet et a un réel donné (ce que j'ai écrit),
avec la Q1 : [tex]f(x)=a(x-82,5)^2+57[/tex] où a est un réel donné.
Compliqué de trouver que [tex]\alpha = \cdots[/tex] et [tex]\beta=\cdots[/tex] ?
Pour le justifier, j'ai écrit : Et donc, aucun calcul à faire (enfin, si, obtenir 82,5 à partir de 165...).
Parce que, supposition sans confirmation, sans réponse, j'avais aussi écrit :
On t'a forcément donné un système d'axes orthonormé dont l'origine est la base du pilier de gauche, moyennant quoi ces coordonnées (α;β) sont à déduire de l'énoncé par simple lecture (le sommet de la courbe est pile au milieu entre les deux piliers)...
Tu as deux points de la courbe de coordonnées (0;0) et (0;165).
De plus le point S (pour sommet) figure sur mon dessin avec [tex]\alpha[/tex] (son abscisse) et [tex]\beta[/tex] son ordonnée.
[tex]\beta[/tex] se lit sur le dessin, c'est la conséquence du fait que la droite représentant le rail est la tangente horizontale en S à la courbe. Faut-il t'expliquer comment obtenir 82,5 à partir de 0 et 165 ?
Voilà pour la Q1
Question 2
Regarde ta leçon et tu verras que selon que le a est >0 ou <0 la courbe se présente comme ceci : [tex]\bigcup[/tex] ou [tex]\bigcap[/tex]. Alors ?
Justifier que a = -0,0084.
Je t'ai écrit : Pour trouver a, tu sais que f(0)=0 , donc...
Tu sais maintenant que [tex]f(x)=a(x-82,5)^2+57[/tex], donc tu dois calculer f(0) et écrire que le résultat trouvé est égal à 0...
Petite équation niveau 4e à résoudre et tu tombes sur a =-0,0084 (*)...
Faut-il t'expliquer comment on calcule f(0) ?
Question 3.
Tu sais maintenant que [tex]f(x)= -0,0084(x-82,5)^2+57[/tex]
Les 2 piliers intermédiaires sont à 49 m et 116 m du 1er pilier.
f(49) est l'ordonnée du point de la courbe d'abscisse x = 49 (voir dessin). Faut-il t'expliquer comment calculer f(49) ?
Sachant que le rail est à 57 m au dessus de la ligne des 2 piliers bétonnés, il te faut - en utilisant f(49) - trouver l'écart entre le rail et le point de la courbe.
@+
[EDIT] (*) -0,0084 mais arrondi à partir de -0,008374665....
Dernière modification par yoshi (22-02-2015 21:56:45)
Arx Tarpeia Capitoli proxima...
Hors ligne
#6 23-02-2015 10:05:14
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonjour,
Retour sur le problème qui m'a tracassé...
Il n'y a qu'une alternative :
* Soit on sait que [tex]f(x)=ax^2+bx+c[/tex] s'écrit aussi [tex]f(x)=a(x-\alpha)^2+\beta[/tex] où [tex](\alpha\;;\;\beta)[/tex] sont les coordonnées du sommet,
* Soit on ne sait pas. Dans ce cas, il faut arriver à le retrouver...
Après réflexions, on peut simplifier la recherche.
On part de f(0)=0
Et on en déduit que c = 0.
On a donc [tex]f(x)=ax^2+bx[/tex]...
Mais vu la forme demandée, on ne peut pas faire l'impasse sur :
1. La mise sous forme canonique (plus simple maintenant).
[tex]f(x) =a\left(x^2+\frac b a x\right)=a\left[\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a^2}\right]=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}[/tex]
2. La connaissance de l'abscisse du sommet : [tex]-\frac{b}{2a}[/tex]
L'ordonnée de ce sommet étant y = 57, [tex]f\left(-\frac{b}{2a}\right)=57[/tex]
D'où [tex]f\left(-\frac{b}{2a}\right)= -\frac{b^2}{4a} =57.[/tex]
On écrit donc [tex]f(x)=a\left(x+\frac{b}{2a}\right)^2+57[/tex]
Et l'abscisse de ce sommet étant [tex]\frac{-b}{2a}=82,5[/tex], on écrit alors :
[tex]f(x)=a\left(x+\frac{b}{2a}\right)^2+57=a\left(x-\frac{-b}{2a}\right)^2+57=a(x-82,5)^2+57[/tex]
-------------------------------------------------
Remarque.
Sans la forme imposée, sachant que
1. [tex]f(x)=ax^2+bx[/tex]
2. [tex]f(165)=0[/tex]
on trouvait "facilement" a et b :
[tex]\begin{cases}82,5^2a+82,5b &=57\\165^2a+165b &=0\end{cases}\;\Leftrightarrow\; \begin{cases}82,5a+b &= \dfrac{57}{82,5}\\165a+b &=0\end{cases}[/tex]
De la deuxième équation on tire [tex]b = -165a[/tex] que l'on reporte ligne 1 (ou on soustrait les 2 lignes membre à membre) :
[tex]82,5a-165a = \dfrac{57}{82,5}\;\Leftrightarrow\; a=-\dfrac{57}{82,5^2}\approx -0,0084[/tex] ([tex]\approx[/tex] et non "=" !!)
Constatant que a était une valeur approchée :
- soit on calculait b en partant de la valeur exacte de a = [tex]-\dfrac{57}{82,5^2}[/tex]
- soit on exprimait a en fonction de b
[tex]a=-\frac{b}{165}[/tex]
D'où [tex]82,5\times \left(-\frac{b}{165}\right)+b=\frac{57}{82,5}[/tex]
[tex]\Leftrightarrow\;b\left(-\frac{1}{82,5}+1\right)=\frac{57}{82,5}[/tex]
[tex]\Leftrightarrow\;\frac{b}{82,5}=\frac{57}{82,5}\Leftrightarrow\;b=57[/tex]
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#7 09-05-2015 18:21:46
- marion2nd
- Invité
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonsoir! J'ai en ce moment un exercice à faire qui correspond à celui là et je n'ai pas compris comment il fallait répondre à la question 1 " Justifier que pour tout réel [tex]x \in I[/tex], on a :
[tex]f(x)=a(x-82,5)^2+57[/tex] où [tex]a[/tex] est un réel fixé."
Est-ce une réponse écrite résumant le cours sur les fonctions polynômes ou un calcul ?
Pour l'instant j'ai repris mon cours en modifiant les coordonnées du sommet de la parabole mais je ne sais pas ce que je dois faire d'autre pour justifier.
Merci
#8 09-05-2015 19:28:51
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonsoir,
La parabole a pour sommet le point S(82,5 ; 57).
Et la forme générale de la fonction f est [tex]f(x) =ax^2+bx+c[/tex].
Ça c'est acquis.
Tu demandes :
Est-ce une réponse écrite résumant le cours sur les fonctions polynômes ou un calcul ?
J'ai déjà répondu à cette question au post #6 où j'ai écrit :
* Soit on sait que [tex]f(x)=ax^2+bx+c[/tex] s'écrit aussi [tex]f(x)=a(x-\alpha)^2+\beta[/tex] où [tex](\alpha\;;\;\beta)[/tex] sont les coordonnées du sommet,
* Soit on ne sait pas. Dans ce cas, il faut arriver à le retrouver...
Mais, je ne suis pas à ta place.
Alors, question :
dans ton cours, est il écrit que :
[tex]f(x)=ax^2+bx+c[/tex] s'écrit aussi [tex]f(x)=a(x-\alpha)^2+\beta[/tex] où [tex](\alpha\;;\;\beta)[/tex] sont les coordonnées du sommet ?
Si oui, c'est immédiat ! Il y a juste à remplacer[tex] \alpha[/tex] et [tex]\beta[/tex] respectivement par 82,5 et 57
Si non, je t'invite à relire le post #6 dans lequel le travail est fait en 2 étapes et qui nécessite la mise sous forme canonique que tu as besoin de connaître...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 09-05-2015 19:53:19
- marion2nd
- Invité
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Re,
Et bien c'est ce qu'il y a dans mon cours j'ai donc fait comme vous l'aviez dit, je trouvais ça bizarre qu'il n'y est pas plus de calcul à faire...
Merci pour votre aide !
#10 10-05-2015 10:13:12
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Re,
Alors, c'est bien....
Si oui, c'est immédiat ! Il y a juste à remplacer α et β respectivement par 82,5 et 57
Il faut quand même au préalable avoir justifié que les coordonnées de ce sommet sont bien (82,5 ; 57), mais normalement ce préalable est automatique...
Petite question ;-) lorsque tu appliques un théorème de Géométrie (par ex.) le redémontres-tu à chaque fois ? ^_^
Mais si vraiment, tu veux faire du calcul, alors il te faut reprendre les calculs des points 1. et 2. du post #6...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#11 10-04-2016 15:24:11
- Anna
- Invité
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Merci beaucoup Yoshi pour ces explications, j'ai un prof de maths qui explique très mal et qui n'a aucune autorité, j'essaye de m'aider de mon manuel mais ca ne marche pas, je comprends rien :')
Tes explications étaient très claires, merci beaucoup ;)
#12 10-04-2016 21:31:53
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : En lien avec l'architecture (Fonction polynôme de degré 2 )
Bonsoir,
content pour toi...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1
Discussion fermée








