Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 26-01-2008 12:38:32
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
tobbogan [Résolu]
coucou voila je suis perdue je ne comprend plus rien si vous pouviez m'aider merci d'avance...
On souhaite réaliser un toboggan reliant la plateforme BB’C’C au sol. Pour cela on se propose de déterminer son profil dans le plan vertical (ABH). Les cotes sont celles indiquées sur les figures. On considère le repère orthonormal (A, i, j) en posant le vecteur i =1/5 vecteur AH. Et vecteur j= ½ vecteur HB.
Ce profil sera une courbe C vérifiant les conditions suivantes.
[1] C passe par les points A, B et I, milieu de [AB]
[2] la fonction h représentée graphiquement par C dans le repère orthonormal (A, i, j) est dérivable sur [0 ; 5] ;
[3] les tangentes A et B à C sont horizontales
1) C peut être : (a) le segment de droite [AB] ? (b) un arc de parabole ? Expliquer
2) On se propose de déterminer deux arcs de parabole AI et IB se raccordant en I dont la réunion formera la courbe C.
a) Soit la fonction f définie sur [0 ; 2.5] par f(x)= ax² + bx + c, (a, b, c étant des réels). Déterminer les réels a, b, c pour que la courbe de f passe par A, I et que la tangente en A soit horizontale.
b) De même on cherche une fonction trinôme du second degré g définie sur [2.5 ; 5] dont la courbe constitue le deuxième arc IB. Ecrire les conditions vérifiées par g. En déduire la fonction g.
c) Vérifier que la courbe C, réunion des deux arcs obtenus dans les deux questions précédentes, réponds aux conditions [1], [2], [3].
d) Construire la courbe C ainsi obtenue dans un repère (échelle 1/50è)
3) Recherche d’un arc du troisième degré
Soit h : x ==>>px³ + qx ² + rx + s une fonction polynôme degré, p, q, r, s réels.
4) a) sachant que la courbe C de h vérifie les conditions [1], [2] et [3] démontrer qu’on obtient le système [S] suivant.
S =0
125p +25q +5r+ s = 2
15.625p + 6.25q + 2.5r + s = 1
R = 0
75p + 10q + r =0
b) En déduire la fonction h. Construire sa courbe C’ dans le même repère qu’à la question 2.
5) Recherche de la pente maximale
a) Déterminer pour chacune des deux courbes obtenues aux questions 2 et 3 la pente maximale des tangentes.
b) On veut que l’angle des tangentes avec (AH) n’excède pas 35°. Quelle courbe choisir ?
Hors ligne
#2 26-01-2008 13:53:23
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonjour Paulinedu29,
Et Bienvenue sur BibM@th...
Nous t'aiderons volontiers si tu précises ton "je suis perdue"... Qu'as-tu été capable de faire ? Qu'est-ce qui t'arrête exactement ? Tu dois bien comprendre que cet exercice est assez long et qu'il y faudra que tu y mettes un peu du tien pour aller jusqu'au bout ;-)
D'autre par, il est ptécisé dans ton énoncé : "les cotes sont celles indiquées sur la figure"... Je n'ai encore pas attaqué le problème mais sans ces cotes 'sauf si elles figurent dans le texte) ça rique d'être difficile...
Où est le point H ? H est-il le projeté orthogonal de B sur l'horizontale passant par A ? Je présume que oui...
Es-tu capable de scanner ton image, de l'uploader sur le site de Imageshack, par exemple, puis de l'afficher dans ton texte ?
S non, si tu scannes l'image tu me l'envoies, en pièce jointe dans unn mail, à : yoshikATno-log.org en remplaçant AT par @, je m'occupe du reste...
En attendant, pour commencer, voici qq biscuits...
Question 1.
Le segment de droite [AB] n'est pas horizontal (A au sol et B sur la plate-forme) : comment pourrait-il y avoir des tangentes horizontales en A et B ?
Question 2a) Un point appartient à une courbe si et seulement ses coordonnées vérifient l'équation de la courbe. A origine des coordonnées donc A(0 ; 0)
Cela signifie que f(0)=0 et donc tu vas déduire la valeur de c.
D'autre part, tu écris que [tex]\vec{j}={1 \over 2}\vec{HB}[/tex], donc : [tex]\vec{HB}=2\vec{j}[/tex]
[tex]\vec{i}={1 \over 5}\vec{AH}[/tex], donc : [tex]\vec{AH}=5\vec{j}[/tex]
Coordonnées de B -- > (5 ; 2) donc Coordonnées de I : --> (5/2 ; 1)
Puisque I est sur la courbe alors f(5/2)=1
Puisque la tangente en A(0 ; 0) à la courbe est horizontale (coeff. dir. nul) alors f'(0)=0
Ces deux lignes te donnent un système de deux équations à deux inconnues te permettant de trouver a et b...
Reviens avec ce que tu auras déjà fait et des questions le cas où...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 26-01-2008 16:12:46
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
Re : tobbogan [Résolu]
je n'arrive rien, je comprend pas l'exercice
Hors ligne
#4 26-01-2008 17:03:20
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Salut,
Alors, on va y aller pas à pas...
Je t'ai écrit :
En attendant, pour commencer, voici qq biscuits...
Question 1.
Le segment de droite [AB] n'est pas horizontal (A au sol et B sur la plate-forme) : comment pourrait-il y avoir des tangentes horizontales en A et B ?
Question 2a) Un point appartient à une courbe si et seulement ses coordonnées vérifient l'équation de la courbe. A origine des coordonnées donc A(0 ; 0)
Cela signifie que f(0)=0 et donc tu vas déduire la valeur de c.
D'autre part, tu écris que [tex]\vec{j}={1 \over 2}\vec{HB}[/tex], donc : [tex]\vec{HB}=2\vec{j}[/tex]
[tex]\vec{i}={1 \over 5}\vec{AH}[/tex], donc : [tex]\vec{AH}=5\vec{j}[/tex]
Coordonnées de B -- > (5 ; 2) donc Coordonnées de I : --> (5/2 ; 1)Puisque I est sur la courbe alors f(5/2)=1
Puisque la tangente en A(0 ; 0) à la courbe est horizontale (coeff. dir. nul) alors f'(0)=0
Ces deux lignes te donnent un système de deux équations à deux inconnues te permettant de trouver a et b...
Qu'est-ce que tu ne comprends pas là-dedans (prière de ne pas répondre : tout ! Ce n'est jamais vrai) ?
Si tu ne poses pas de questions précises sur ce qui te gêne, ce que tu ne comprends pas, on n'avancera pas...
Donc je répète : qu'est-ce que tu ne comprends pas dans les indications que je t'ai données ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 26-01-2008 18:10:41
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
Re : tobbogan [Résolu]
je comprend t reponse mais le reste de lexo je navance a rien
Hors ligne
#6 26-01-2008 20:40:07
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonsoir,
Attention, pas de sMS !
Bon, si le "m'amusais" à être aussi laconique que toi dans mes réponses, tu serais bien ennuyée.
Si t'as comprios ce que je t'ai expliqué,n alors on continue...
Question 2 b)
Si je relis les conditions de départ
[3] les tangentes A et B à C sont horizontales
Ca veut donc dire que ta fonction trinôme du 2nd degré, appelons-la g qui est telle que g(x)=ax²+bx +c admets une tangente horizontale en B, donc g'(5)=0, ce qui te permettra d'écrire b en fonction de a... (*)
dont la courbe constitue le deuxième arc IB
Ca, ça veut dire que les coordonnées des points I et B vérifient l'équation de la courbe puisque cette courbe passe par I et B.
Avec I(5/2 ; 1) on a donc g(5/2) = 1 ce qui va te donner une 2e équation à 3 inconnues a b et c, celle-là
Avec B(5 ; 2), on a donc g(5) = 2 ce qui va te donner une 3e équationn "halement à 3 inconnues a b et c...
Dans les 2 équations ci-dessus, tu vas remplacer b par son expression en fonction de a, obtenue un plus haut, ici (*).
Tu auras ainsi éliminé une inconnue, il ne te restera plus alors qu'à résoudre le système de 2 équations à 2 inconnues, a et c, pour pouvoir écrire enfin g(xà avec des coefficients numériques...
Question 2 c) et d) --> évident.
Avant d'aller plus loin, il serait bon que tu fasses part de tes résultats, sinon ça ne sert à rien... Allez, un pettit effort, tu veux bien ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#7 27-01-2008 10:47:22
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonjour,
Voilà l'image : comme ça on a des certitudes. Merci.
Et où es-tu de tes calcils ? Montre-nous ça qu'on te dise si c'est bon ou pas...
@+
[EDIT] Secoue-toi un peu : je viens de faire (et finir) réellement ton exo (dessins compris) et si on veut aller au bout des explications, à ce rythme, on n'est encore loin d'être rendus ! ;-)
Dernière modification par yoshi (27-01-2008 11:47:33)
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 29-01-2008 19:27:53
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
Re : tobbogan [Résolu]
bonsoir,
pour mes calculs, j'ai trouvée ça mais je ne pense pas que cela soit correcte,
2)a) a=2 b=0 c=0
b)y=f(x)=ax^2 + bx + c
y=f(x)
y+1 = f(x + 5/2)
y = f(x + 5/2) - 1
f(x + 5/2) - 1 = ax^2 + bx + c
f(x) = a(x - 5/2)^2 + b(x - 5/2) + c +1
a=2 b=0 c=0
f(x)=2(x-5/2)^2 +1
voila
Hors ligne
#9 29-01-2008 20:41:23
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonsoir Paulinedu29,
Je désespérais...
Bon, il y a de grosses confusions dans les notations...
Alors x est l'abscisse et f(x) l'ordonnée.
La courbe passe par A(0 ; 0). Donc les coordonnées de A vérifient l'équation de la courbe : ça veut dire ici que f(0) = 0
Donc f(0) = a X 0² + b X 0 + c = 0. On obtient donc c = 0.
f(x) s'écrit donc en fait f(x) = ax²+bx
La tangente en A à la courbe est horizontale.
La pente de la tangente en un point c'est la valeur de la dérivée en ce point.
f'(x)=2ax+b. Donc au point A d'abscisse 0, la valeur de la dérivée est f'(0) = b. Or la tangente est horizontale, ça veut dire que sa pente est nulle. Donc f'(0)=0, donc b = 0
Et l'équation de ta courbe s'écrit maintenant f(x)=ax²
Reste à trouver a.
Donc tu n'as pas y+1 = f(x+5/2), mais f(5/2)=1 (Pour I x = 5/2 et y = 1)
Pour calculer f(5/2) on remplace dans ax²+bx+c, x par 5/2 et on écrit que ça vaut 1 :
[tex]a\times ({5 \over 2})^2=1\;donc\;a\times{25 \over 4}=1\;et\;encore\:25a=4\;soit\;a={4 \over 25}[/tex]
On peut donc écrire :
[tex]f(x)={4\over 25}x^2[/tex]
Pour g, on recommence le travail.
* La tangente en B(5 ; 2) est horizontale, donc g'(5)=0
On pose g(x)=ax²+bx+c, donc g'(x)=2ax+b. Et g'(5)=0 se traduit par 2a X 5 + b =0. Première équation
* La courbe passe par I(5/2 ; 1), donc g(5/2)= 1. Ce qui donne :
[tex]a\times({5 \over 2})^2+b\times{5 \over 2}+c=1\;soit\;encore\;{25 \over 4}a+{5 \over 2}b+c=1[/tex]
Comme je sais qu'il y a plein de gens à qui les fractions donnent des boutons, je mulltiplie les 2 membres par 4 :
[tex]25a+10b+4c=4[/tex] Deuxième équation.
* La courbe passe par B(5;2), donc g(5)=2 :
[tex]a\times 5^2+b\times 5+c=2\;soit\;25a+5b+c=2[/tex]Troisième équation.
Tu as donc 2 équations et 3 inconnues... Heureusement la première équation permet de savoir que b = -10a
Je remplace donc dans la 2e et la 3e équation, b par -10a et on tombe sur un systèùe de deux équations à deux inconnues a et c de niveau 3e...
AU boulot pour le résoudre...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#10 29-01-2008 21:49:57
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
SAlut,
J'ai vu que tu as pris connaissance de ma réponse.
Pour te permettre de vérifier tes calculs, voilà g(x) :
[tex]g(x)={-}{4 \over 25}x^2+{8 \over 5}x-2[/tex]
La suite paer moi, demain.
Si qq d'autre passe et que tu as répondu, qu'il ne se gêne surtout pas !...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#11 30-01-2008 19:11:54
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
Re : tobbogan [Résolu]
jé trouvé
===> a=37/20
b=-37/2
c=-111/16 pour les inconnus
Hors ligne
#12 30-01-2008 21:41:28
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonsoir Paulinedu29,
Hélas, non ! Le résultat est au dessus de ton post depuis hier soir...
Correction.
Les équations sont :
[tex]\begin{cases}10a+b&=0\\25a+10b+4c&=4\\25a+5b+c&=2\end{cases}[/tex]
De la première équation on tire b=-10a et maintenant on va remplacer b par -10a dans la 2e et la 3e équation :
[tex]\begin{cases}25a-100a+4c&=4\\25a-50a+c&=2\end{cases}[/tex]
On simplifie les a :
[tex]\begin{cases}-75a+4c&=4\\-25a+c&=2\end{cases}[/tex]
Maintenant je résous ce système niveau 3e par la méthode de combinaison (ou addition) : je multiplie les deux membres de la deuxiième équation par -3 :
[tex]\begin{cases}-75a+4c&=4\\75a-3c&=-6\end{cases}[/tex]
J'additionne membre à membre (les a s'éliminent) et j'obtiens :
c = -2
Je reprends la deuxième équation avant d'avoir multiplié par -3 et je remplace c par -2 :
-25a -2 = 2 d'où -25a = 4 et donc :
[tex]a={-}{4 \over 25}[/tex]
Comme je sais que b = -10a, je fais :
[tex]b=-10\times({-}{4 \over 25})={40 \over 25}={8 \over 5}[/tex]
D'où :
[tex]g(x)={-}{4 \over 25}x^2+{8 \over 5}x-2[/tex]
On va passer tout de suite à la 3e question.
[tex]h(x)=px^3+qx^2+rx+s[/tex]
Cette courbe passe par A(0 ; 0) et B(5 ; 2)
Donc h(0)=0 et h(5) = 2 ;
[tex]h(0)=p.0^3+q.0^2+r.0+s=0[/tex]
[tex]h(5)=p.5^3+q.5^2+r.5+s=2[/tex]
Cette courbe passe par I(5/2 ; 1) donc h(5/2)=1 :
[tex]h\left(\frac 5 2\right)=p\left(\frac 5 2\right)^3+q\left(\frac 5 2\right)^2+r\left(\frac 5 2\right)+s=1[/tex]
ou encore :
[tex]h\left(\frac 5 2\right)=p\left(\frac{125}{8}\right)+q\left(\frac{25}{4}\right)+r\left(\frac 5 2\right)+s=1[/tex]
Tu noteras que 125/8 = 15,625 ; 25/4 = 6,25 et 5/2 = 2,5 on retrouve bien l'énoncé.
Enfin, les tangentes en A et B sont horizontales donc dérivée nulle en ces points :
[tex]h'(x)=3px²+2qx+r[/tex]
Et h'(0)=0 pour A et h'(5)=0 pour B.
Tu n'as qu'à remplacer...
Reviens vite nous dire ce que tu as fait, ce que tu ne comprends pas...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#13 30-01-2008 22:10:04
- paulinedu29
- Membre
- Inscription : 26-01-2008
- Messages : 8
Re : tobbogan [Résolu]
comment fait-on pour la question 2c)
Hors ligne
#14 31-01-2008 10:29:59
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : tobbogan [Résolu]
Bonjour,
C'est le plus facile.
On va appeler C1 la courbe représentative de f er C2 celle de g.
C1 respecte une moitié de la condition (1) : passe par A et I.
C2 respecte l'autre moitié de la condition (1) : passe par B et I.
Conclusion pour C, réunion de C1 et C2 ?
f et g sont deux fonctions polynômes du 2nd degré : elles sont donc toutes deux dérivables sur ]-oo ; + oo[, donc f est forcément dérivable sur [0 ; 5/2] et g sur [5/2 ; 5]. Donc la la fonction représentée graphiquement par C dans le repère orthonormal (A, i, j) est dérivable sur [0 ; 5].
La courbe C1 répond à une partie de la condition (3) : elle admet une tangente horizontale en A.
La courbe C2 répond à l'autre partie de la condition (3) : elle admet une tangente horizontale en B.
Conclusion Pour C, réunion de C1 et C2 ?

C1 en rouge, C2 en bleu et C' en vert. (*)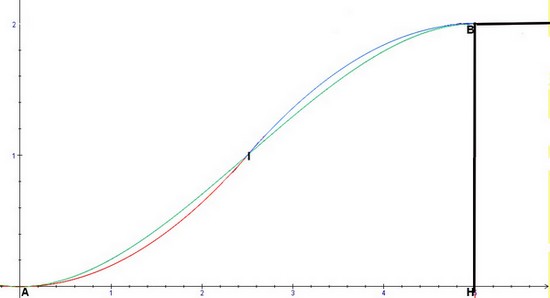
Question 4)
Tu peux constater que l'énoncé te donne (en te demandant de le montrer) r=0 et s =0.
Ta fonction h est donc telle que :
[tex]h(x)=px^3+qx^2[/tex].
Pour trouver p et q, tu vas reprendre les équations données (mais que tu as dû tablir en suivant les indications de mes précédents posts) et y remplacer systématiquement r et s par 0 : tu obtiens ainsi un système de deux équations à 2 i,connues (qui sont p et q) du ype 3e que tu vas résoudre.
Solution :
[tex]h(x)={-}{4 \over 125}x^3+{6 \over 25}x^2[/tex].
Question 5.
La plus difficile
Pente maximum.
La pente en un point, c'est le coefficient directeur de la tangente en ce point, c'est la valeur de la dérivée en ce point.
Donc pour C1, tu calcules f'(x) et sur [ ; 5/2], tu tâches de montrer pour quelle valeur de x, f'(x) est maximum.
Même chose pour C2 et g.
Tu vas trouver la même valeur.
Même chose pour C' et h... Seul petit problème h'(x) et encore du second degré. Et donc la question se pose : pour quelle valeur de x, f'(x) admet-elle un maximum ?
Donc, calcul de la dérivée de h'(x) qui va être du premier degré (comme les fonctions affines) et tu regardes pour quelle valeur de x elle s'annule : c'est encore la même que précédemment...
Je note cette valeur de x : x1.
Tu vas calculer f'(x1), g'(x1) et h'(x1).
Tu vas voir d'ailleurs que f'(x1)=g'(x1)...
La pente d'une droite, c'est aussi la tangente de l'angle que fait cette droite avec l'axe des abscisses...et lequel des 2 angles est inférieur à 35°, tu dis passer pat la touche Tan-1 de ta calculette...
Tu vois qu'il fallait se bouger : c'était assez long.
Questions ?
@+
[EDIT](*) La courbe d'origine ayant disparu, je pense l'avoir retrouvée sur ma machine et je l'ai ré-uploadée chez un autre hébergeur.
Si par hasard, ce n'était pas la bonne, me le signaler SVP.
Merci.
Dernière modification par yoshi (29-05-2017 11:54:16)
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1
Discussion fermée








