Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
#1 02-12-2020 00:37:08
- PatrickLL
- Membre
- Inscription : 01-12-2020
- Messages : 4
Formule de géométrie ??
Bonsoir à toutes et tous,
Je ne suis pas sûr de poster dans la bonne catégorie donc n'hésitez pas à déplacer mon sujet.
Je suis journaliste hippique débutant et une question me trotte dans la tête (oui, je sais, c'est facile ? ). Je ne vous cache pas que j'ai tenté un autre forum dédié aux mathématiques où je me suis fais balader. J'espère que vous pourrez m'aider !
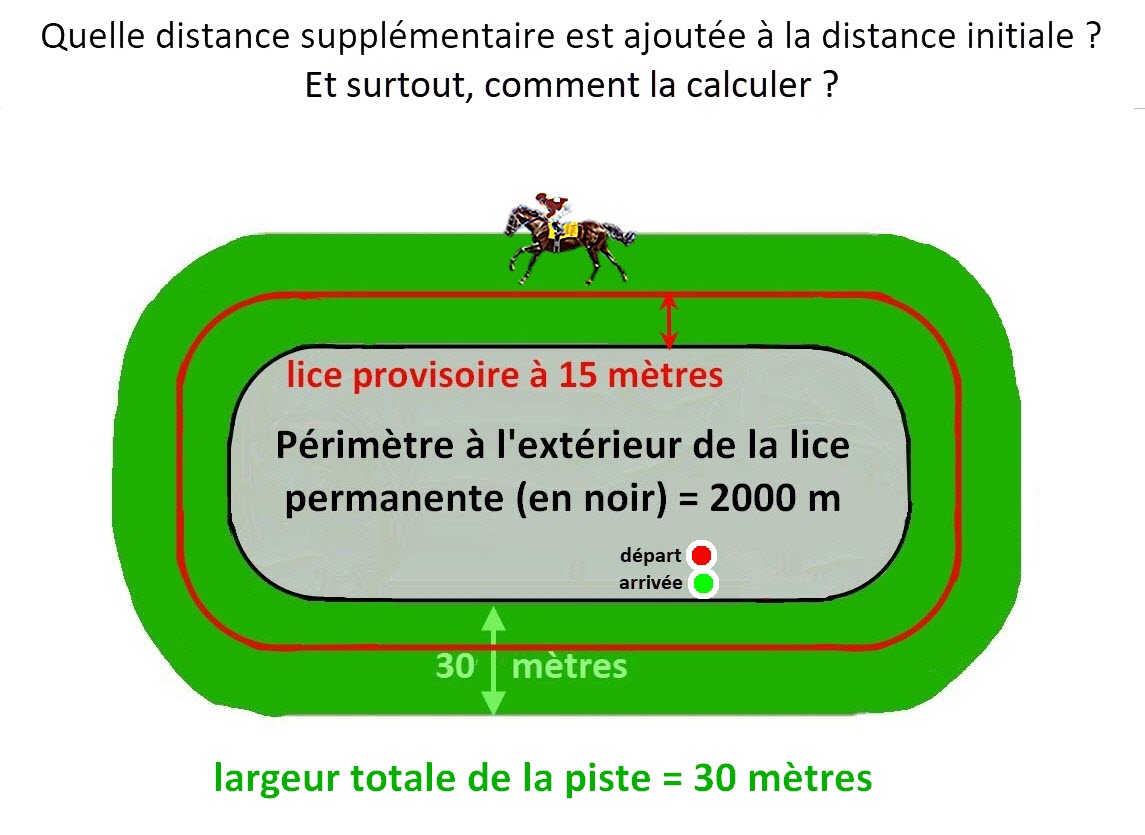
Soit un champ de course et sa piste de, par exemple, de 2000 mètres mesurés à la lice (barrière) permanente en NOIR.
Pour préserver une partie de cette piste, elle est "cordée", c'est-à-dire qu'une lice provisoire en ROUGE, à 15 mètres est ajoutée à l'extérieur.
Les chevaux vont devoir parcourir une distance supplémentaire de quelques dizaines de mètres, mais combien ?
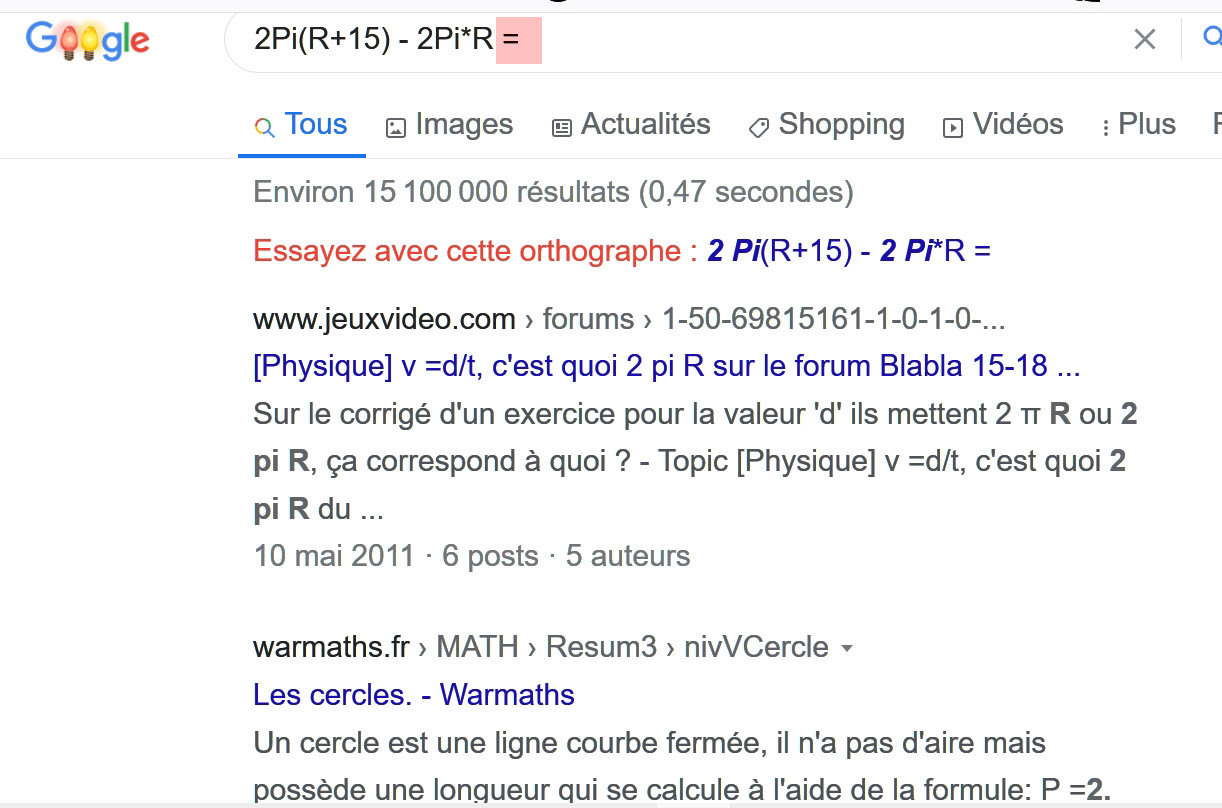
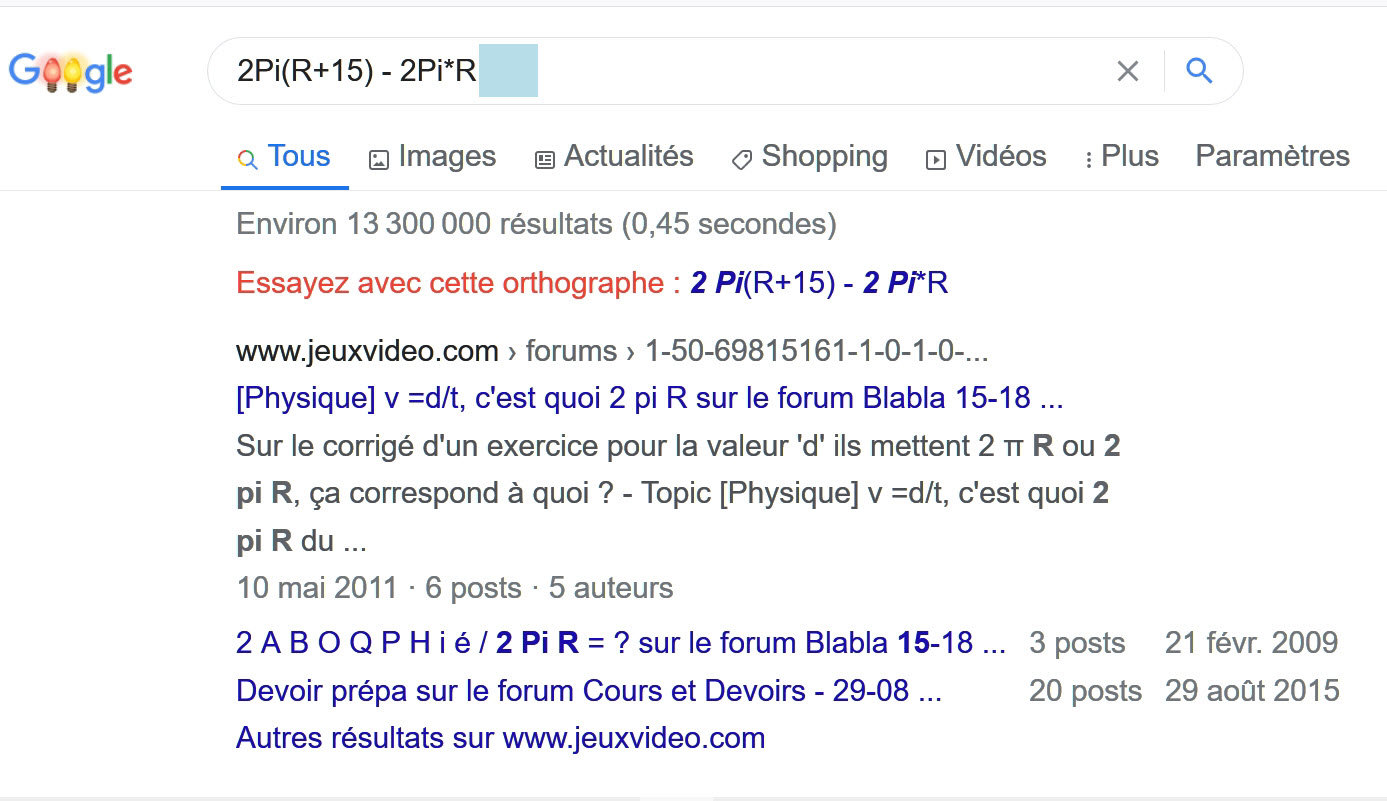
Sur «l'autre forum» on m'a donné cette formule 2Pi(R+15) - 2Pi*R qui ne donne pas de résultat sur Google à part ce que montrent les captures d'écran.
Qui peut m'aider ? Merci d'avance !
Une image vaut 1000 mots paraît-il... en voici 3. La première est mon très modeste montage, les seconde et troisième sont les captures d'écran de la formule avec et sans le signe =.
Dernière modification par PatrickLL (02-12-2020 00:42:16)
Hors ligne
#3 02-12-2020 13:11:07
- Matou
- Invité
Re : Formule de géométrie ??
Bonjour,
si je comprends bien, la lice noire, c'est un "rectangle avec des bords arrondis" et idem pour la rouge.
Pour les parties droites, que l'on soit sur la lice noire ou sur la lice rouge, la distance à parcourir est la même.
Donc, il faut se concentrer sur les parties arrondies. Il y a quatre quarts de cercles sur ta figure, on pourrait travailler sur un seul quart et multiplier par 4 ensuite. Si tu réfléchis bien, on voit qu'il suffit de travailler sur un seul cercle en entier.
Le cercle initial a un rayon R, dont on ne connaît pas la valeur, mais ce n'est pas grave. Son périmètre est $2 \cdot \pi \cdot R$.
LE fait de passer de la lice noire à la rouge est équivalent à augmenter le rayon du cercle de 15 m. Le périmètre devient donc $2 \cdot \pi \cdot (R+15)$ et la différence entre les deux valeurs est $2 \cdot \pi \cdot 15$ (exprimée en mètres).
En conséquence, le passage de la lice noire à la lice rouge se traduit par une augmentation de la distance courue par les chevaux de $2 \cdot \pi \cdot 15$ m.
Cordialement
Matou
#4 02-12-2020 13:30:37
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Formule de géométrie ??
Bonjour,
ça devient lassant tous ces gens qui postent sur plusieurs forums en même temps :
ça ne se fait pas, c'est très mal vu...
Pourquoi essayer de manger dans les assiettes des copains, la tienne ne te suffit pas ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 02-12-2020 16:48:47
- PatrickLL
- Membre
- Inscription : 01-12-2020
- Messages : 4
Re : Formule de géométrie ??
Bonjour,
si je comprends bien, la lice noire, c'est un "rectangle avec des bords arrondis" et idem pour la rouge.
Pour les parties droites, que l'on soit sur la lice noire ou sur la lice rouge, la distance à parcourir est la même.
Donc, il faut se concentrer sur les parties arrondies. Il y a quatre quarts de cercles sur ta figure, on pourrait travailler sur un seul quart et multiplier par 4 ensuite. Si tu réfléchis bien, on voit qu'il suffit de travailler sur un seul cercle en entier.
Le cercle initial a un rayon R, dont on ne connaît pas la valeur, mais ce n'est pas grave. Son périmètre est $2 \cdot \pi \cdot R$.
LE fait de passer de la lice noire à la rouge est équivalent à augmenter le rayon du cercle de 15 m. Le périmètre devient donc $2 \cdot \pi \cdot (R+15)$ et la différence entre les deux valeurs est $2 \cdot \pi \cdot 15$ (exprimée en mètres).En conséquence, le passage de la lice noire à la lice rouge se traduit par une augmentation de la distance courue par les chevaux de $2 \cdot \pi \cdot 15$ m.
Cordialement
Matou
Bonjour Matou,
Plates excuses de ne pas être matheux et de ne pas m'exprimer dans votre langage !
Tu dis que R n'a pas de valeur, j'ai envie de dire que si, puisque la lice noire permanente est à + zéro mètre.
Quelle est la signification de 2⋅π⋅15 m en termes que le simple mortel que je suis puisse comprendre ?
Quand tu écris :
à part "périmètre", c'est du charabia pour moi.
C'est comme si je te disais par exemple que ""le 711 a baissé de valeur parce qu'il rendait trop de poids dans un handicap déclassé et que le handicapeur tente de rétablir l'équilibre dans la listed en tant que supplémenté puisque ne bénéficiant pas de l'avantage donné par l'apprenti"" c'est limpide pour moi mais pas pour toi sauf si tu tu es turfiste chevronné !
Cordialement,
Patrick.
Dernière modification par PatrickLL (02-12-2020 16:52:01)
Hors ligne
#6 02-12-2020 17:50:35
- Matou
- Invité
Re : Formule de géométrie ??
Bonjour,
Je n'ai pas dit que R n'a pas de valeur, mais qu'on ne connaît pas sa valeur. C'est assez différent.
Par exemple, je sais que les chevaux ont une cote mais je ne la connais pas car je ne joue pas aux courses.
J'ajoute ensuite que de toutes façons, ce n'ai pas grave de ne pas connaître R puisque sa valeur n'intervient pas dans le résultat final.
Quant à $2 \cdot \pi \cdot 15$ m, on va commencer par la fin :
m, c'est pour dire que l'unité utilisée est le mètre (sur ton dessin, tu a bien mis 15 mètres).
$2$,$\pi$ et $15$ sont trois nombres et le point ($\cdot$) entre les nombres est un symbole souvent utilisé pour dire qu'on multiplie ces trois nombres. J'aurais pu mettre un signe $\times$, mais je trouve que $\cdot$ est plus joli. $\pi$, c'est le nombre égal à peu près à 3,14 que tu utilises depuis le secondaire pour calculer le périmètre d'un cercle.
Voilà, je te laisse faire les calculs (d'ailleurs, ils sont déjà faits sur un autre site).
Cordialement
Matou.
#7 02-12-2020 19:30:11
- PatrickLL
- Membre
- Inscription : 01-12-2020
- Messages : 4
Re : Formule de géométrie ??
Je n'ai pas dit que R n'a pas de valeur, mais qu'on ne connaît pas sa valeur. C'est assez différent.
Très juste. Nuance que je n'avais pas percuté. Mais elle est connue.
Par exemple, je sais que les chevaux ont une côte mais je ne la connais pas car je ne joue pas aux courses.
C'est cote sans ^ juste au cas où tu veuille te lancer.
J'ajoute ensuite que de toutes façons, ce n'ai pas grave de ne pas connaître R puisque sa valeur n'intervient pas dans le résultat final.
Ok. Pour ma gouverne, est-ce que j'ai tout faux si je dit que, en l'occurrence, la valeur de R = zéro ?
Quant à $2 \cdot \pi \cdot 15$ m, on va commencer par la fin :
m, c'est pour dire que l'unité utilisée est le mètre (sur ton dessin, tu a bien mis 15 mètres).
$2$,$\pi$ et $15$ sont trois nombres et le point ($\cdot$) entre les nombres est un symbole souvent utilisé pour dire qu'on multiplie ces trois nombres. J'aurais pu mettre un signe $\times$, mais je trouve que $\cdot$ est plus joli. $\pi$, c'est le nombre égal à peu près à 3,14 que tu utilises depuis le secondaire pour calculer le périmètre d'un cercle.
.
Oui m pour mètre heureusement je le sais.
Le • est certes plus joli mais incompréhensible pour moi. Tu aurais utilisé * j'aurais compris.
Et π = 3,1415 et des brouettes.
Donc la distance supplémentaire à parcourir, dans le cadre de cette forme d'hippodrome (certains sont multi-pistes avec 3 ou 5 tournants, larges ou serrés) est :
2Pi(R+15) - 2Pi*R
2×3,1415×(0+15)-2×3,1415×0=94,245 mètres en plus.
Hors ligne
#8 02-12-2020 21:51:04
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Formule de géométrie ??
Bosoir,
Pourquoi vouloir absolument effectuer ce calcul-ci :
$2\pi(R+15)-2\pi R$ ?
Matou a montré à partir de cette écriture, qu'en développant cette partie (i.e en multipliant R et 15 chacun par $2\pi$ et en additionnant les résultats), on arrive à :
$\underbrace{2\pi(R+15)}-2\pi R= 2\pi R+2pi\times 15 -2\pi R$
Et on constate qu'on ajoute $30\pi$ à $2\pi R$, pour avoir ensuite l'immense plaisir de soustraire ensuite $2\pi R$ au résultat..
Autant alors supprimer $2\pi R$ (En effet : $2\pi R-2\pi R =0)$ et ne garder que $30\pi$ (On appelle ça : réduire une expression algébrique)
On a donc : $2\pi(R+15)-2\pi R= 2\pi R+2\pi\times 15 -2\pi R =30\pi$
Peu importe donc le rayon initial, quelle que soit sa valeur, le résultat final reste le même.
Quelques exemples numériques :
je prends $\pi \approx 3.1416$ et non 3.1415, parce que derrière le 5, il y a un 9 et que l'arrondi à 0,0001 près doit se faire à 3.1416 qui est une valeur plus proche de 3,14159 que 3,1415.
$2\pi(R+15)\quad\quad -\quad\quad 2\pi R$ $30\times \pi$
$2\times 3.1416(\;\;20+15)-2\times 3.1416\times\;\;20 =\;\; 219.912 - 125.664 = 94.248\quad\quad 30 \times 3.1416 = 94.248 $
$2\times 3.1416(\;\;50+15)-2\times 3.1416\times\;\;50 =\;\; 408.408 - 314.16\; = \,94.248\quad\quad 30 \times 3.1416 = 94.248 $
$2\times 3.1416(\;\;80+15)-2\times 3.1416\times\;\;80 =\;\; 596.904 - 502.656 = 94.248\quad\quad 30 \times 3.1416 = 94.248 $
$2\times 3.1416(110+15)-2\times 3.1416\times 110 =\;\; 785.4 \;\;\;\;- 691.152 = 94.248 \quad\quad 30 \times 3.1416 = 94.248 $
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 03-12-2020 00:46:50
- PatrickLL
- Membre
- Inscription : 01-12-2020
- Messages : 4
Re : Formule de géométrie ??
Bonsoir Yoshi,
Je ne comprends pas un traître mot de ce que tu écris. C'est du chinois pour moi. En fait non, c'est du chinois mâtiné de russe mâtiné de japonais et de je ne sais quoi d'autre.
J'ai très bien compris que j'ai affaire à des pointures et je conçois très bien que c'est lassant tous ces gens comme moi qui postent sur plusieurs forums en même temps... ça ne se fait pas, paraît-il... c'est très mal vu, paraît-il...
Tu aimerais savoir pourquoi essayer de manger dans les assiettes des copains, la tienne ne te suffit pas ? Bin non, ça ne me suffit pas, puisque toutes super pointures que vous, voire des génies (et je n'ai pas de doute quant à vos performances en mathématiques), de ce que je constate sur mon sujet, tu imposes ton grand savoir saupoudré d'un chouïa de mépris, à quelqu'un qui de toute façon n'est pas capable de le remettre en question. En ce qui concerne les mathématiques du moins.
Et moi qui croyait, naïvement, obtenir une aide simple qui soit compréhensible de tous les simples mortels comme moi et des millions d'autres...
Rassure-toi, je ne vais pas te lasser + longtemps. Je vais chercher mon bonheur ailleurs.
Merci (grand) à @Matou qui a pris le temps d'essayer de comprendre mon point de vue.
Yoshi fais-toi plaisir et à moi aussi, clos mon sujet et supprime mon compte. Bon vent.
Hors ligne
#10 03-12-2020 08:44:23
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Formule de géométrie ??
Bonjour,
Oulah, oulah, oulah...
Je n'ai jamais injurié personne !
En l'occurrence, ici, j'ai essayé de me monter simple, clair et didactique : aucun mépris, aucune suffisance de ma part : j'ai même parfois traduit le vocabulaire mathématique...
Rien, mais alors rien de génial dans ce que j'ai écrit et ça nez vole même pas très haut : je veux bien comprendre que quelqu'un qui trouve les mathématiques comme indigestes, qui s'y perd facilement ait des difficultés : j'ai toujours préféré bosser avec quelqu'un qui a des difficultés mais qui a un désir sincère de comprendre qu'avec celui qui a plus de facilité et qui ne veut pas faire d'efforts.
Donc, je ne vois pas à quoi tu fais allusion.
Chaque demandeur d'aide est un cas à part : t'ai-je fait la moindre remarque sur le fait que tu avais posté ailleurs avant ?
Bin oui, c'est très mal venu sur les forums : certains ont même inscrit cela avec blocage immédiat du compte dans leur charte de fonctionnement.
Ceux iui le font, en général, se servent des corrections des uns pour se parer des plumes du paon auprès des autres j'ai trouvé ceci, j'ai trouvé cela !...
Aurais-je dû ? Non, parce que je traite au cas par cas.
Tu dois être probablement influencé par une discussion récente où un quidam me trouve dur et m'accuse de tenir des proposas aberrants. Depuis 15 ans que je suis là, c'est bien la première fois.
Je vais tâcher de trouver 1/45 h pour lui répondre point par point pour lui montrer pourquoi il m'a trouvé dur...
Un dernier mot : je suis capable de reconnaître mes torts, lorsque j'en ai, sinon j'aurais été un très mauvais pédago...
Il faut quand même que tu saches et ça ne risque de ne pas te faire plaisir, mais je ne peux pas laisser passer que tu me montres du doigt en disant que je suis incapable de me mettre au niveau de mon interlocuteur : les notions que j'ai essayé d'expliciter sont du niveau de la classe de 5e...
Aurais-je dû les passer sous silence ?
Peut-être, l'enfer est pavé de bonnes intentions dit-on...
J'ai souhaité Bon vent à quelqu'un un jour, il l'a mal pris.
Alors j'explicite : que les vents te soient favorables et te portent là où tu te le souhaites, sans encombre.
Quant à moi, je n'ai pas besoin du vent ; je reste là ! ;-)
Sans rancune.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1








