Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 29-11-2020 20:57:38
- benjamin94270
- Invité
Trajectoire d'une table 4 pieds sur roulettes
Bonsoir,
(On n'est pas des sauvages !)
---------------------------------------------
Voici le problème :
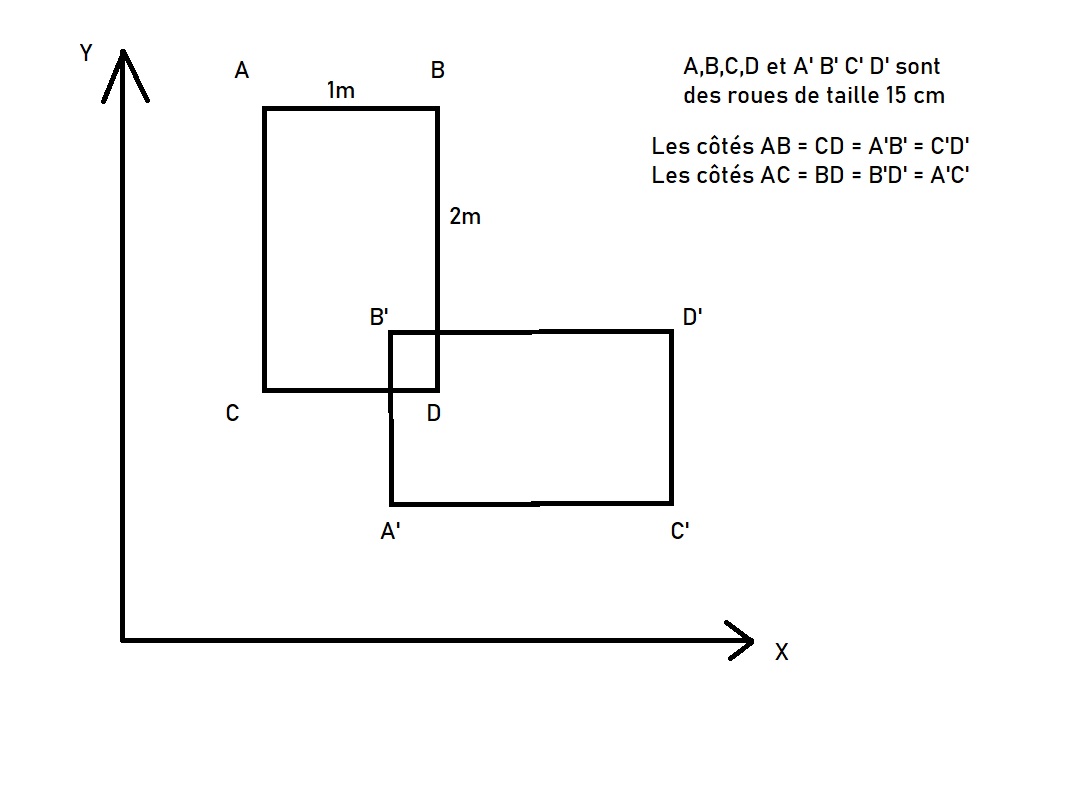
Les points d'une table A, B, C et D sont des roues fixes de diametre 20 cm. La table doit rouler de sa position ABCD vers A'B'C'D' avec des roues fixes.
Quels sont les angles des roues à prendre en compte pour que la rotation soit parfaite ?
 -------------------------------------------------
-------------------------------------------------
Merci
Dernière modification par yoshi (29-11-2020 22:49:20)
#2 30-11-2020 10:06:02
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Trajectoire d'une table 4 pieds sur roulettes
Bonjour,
Le mouvement de la table résulte, dans le cas le plus simple, de la superposition:
a) d'un mouvement de translation uniforme du barycentre entre les positions extrêmes (G, G'), à la vitesse VG = (1/t).GG' ;
b) d'un mouvement de rotation uniforme autour de la position instantanée du barycentre, faisant tourner l'objet d'un angle droit dans le sens antihoraire et s'effectuant à la vitesse angulaire ω = π/2t ;
ce dernier mouvement communique à chaque pied une vitesse d'entraînement normale à la diagonale, orientée vers la gauche de l'observateur placé en (G), et pourvu de la norme Ve = Rω = πR/2t (en convenant de poser
R = GA = GB = GC = GD = (1/2)(AB2 + AC2)1/2 = 51/2/2 ).
La vitesse absolue de chaque pied par rapport au sol, qui détermine l'orientation spontanée des roues montées sur un support mobile, résulte de la composition des deux vitesses précédentes: si l'on convient de caractériser les pieds (Pi) par les indices (1, 2, 3, 4) et de faire intervenir le vecteur rotation
Ω = (0, 0, ω) = ω.Uz
il vient:
Vi = VG + ΩΛGPi .

Il faudrait vérifier si pour toute position intermédiaire de la table, les roues présentent par rapport à l'objet une orientation constante, autrement dit si l'angle (GPi, Vi) demeure constant, ce que paraît supposer la dernière question de l'énoncé:
Quels sont les angles des roues à prendre en compte pour que la rotation soit parfaite ?
Dernière modification par Wiwaxia (27-12-2020 15:33:36)
Hors ligne
#3 30-11-2020 10:07:24
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Trajectoire d'une table 4 pieds sur roulettes
Bonjour,
Le mouvement de la table résulte, dans le cas le plus simple, de la superposition:
a) d'un mouvement de translation uniforme du barycentre entre les positions extrêmes (G, G'), à la vitesse
VG = (1/t).GG' ;
b) d'un mouvement de rotation uniforme autour de la position instantanée du barycentre, faisant tourner l'objet d'un angle droit dans le sens antihoraire et s'effectuant à la vitesse angulaire ω = π/2t ;
ce dernier mouvement communique à chaque pied une vitesse d'entraînement normale à la diagonale, orientée vers la gauche de l'observateur placé en (G), et pourvu de la norme Ve = Rω = πR/2t (en convenant de poser
R = GA = GB = GC = GD = (1/2)(AB2 + AC2)1/2 = 51/2/2 ).
La vitesse absolue de chaque pied par rapport au sol, qui détermine l'orientation spontanée des roues montées sur un support mobile, résulte de la composition des deux vitesses précédentes: si l'on convient de caractériser les pieds (Pi) par les indices (1, 2, 3, 4) et de faire intervenir le vecteur rotation
Ω = (0, 0, ω) = ω.Uz
il vient:
Vi = VG + ΩΛGPi .

Il faudrait vérifier si pour toute position intermédiaire de la table, les roues présentent par rapport à l'objet une orientation constante, autrement dit si l'angle (GPi, Vi) demeure constant, ce que paraît supposer la dernière question de l'énoncé:
Quels sont les angles des roues à prendre en compte pour que la rotation soit parfaite ?
Dernière modification par Wiwaxia (30-11-2020 10:09:17)
Hors ligne
#4 30-11-2020 10:56:48
- jpp
- Membre
- Inscription : 31-12-2010
- Messages : 1 105
Re : Trajectoire d'une table 4 pieds sur roulettes
salut ,
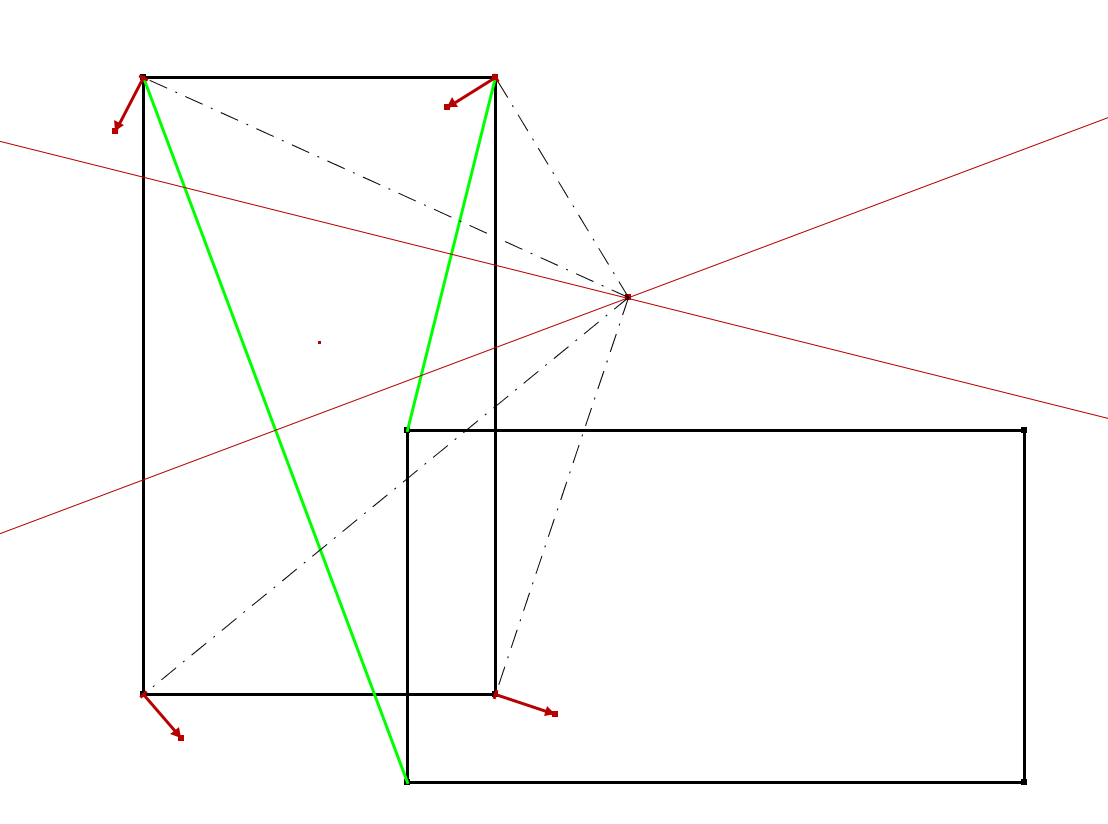
Uniquement , si l'intersection des 2 rectangles est un carré de diagonale : B'D , alors le CIR (centre instantané de rotation) de la table qui va être fixe dans ce cas , est le point d'intersection des médiatrices de [BD] et [B'D'] . on l'appellera O .
Les droites (OA) , (OB) , (OC) & (OD) sont les axes de rotation des 4 roues fixes .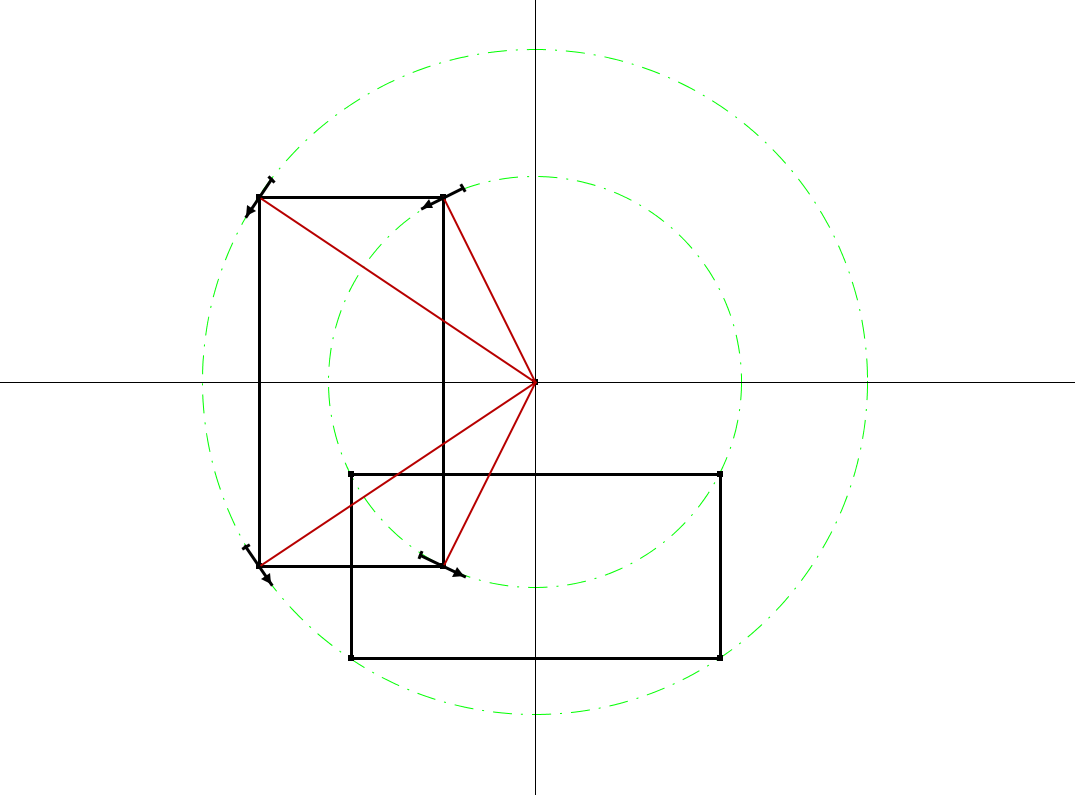
En général on trace deux médiatrices de [AA'] & [BB'] par exemple . Et leur point de concours est le centre de rotation recherché .
Et les 4 vecteurs donnent l'orientation de chacune des roues .
Dernière modification par jpp (30-11-2020 11:55:13)
Hors ligne