Forum de mathématiques - Bibm@th.net

Colin

Invité

Math vecteurs

Bonjours , demain j’ai un contrôle je m’entraîne avec des exos mais celui la je n’en n’est pas vraiment fait avant et je n’y arrive pas vraiment pouvez vous me le résoudre en me l’expliquant si vous le voulez bien  , pour que je puisse en faire d’autre et vous les montrer merci ,,,

A(0;5)     B(-2;1)      C(5;4)

a)Déterminé les coordonnées du vecteur AB
b)Déterminé les coordonnées du point D tel que
ABCD soit un parallélogramme
c)Calculer les coordonnées du centre de ce parallélogramme

Voilà je sais qu’il faut faire un schéma fin dessin ect désolé de ce dérangement je préfère demander et réussir mon contrôle que de ne rien dire et avoir une mauvaise note !

yoshi

Modo Ferox

Inscription : 20-11-2005

Messages : 16 991

Re : Math vecteurs

Bonjour,

En appelant à l'aide un dimanche soir à 22 h, dernier jour de tes vacances, pour le lendemain 8 h, espérais-tu vraiment avoir une réponse ?
Si oui, alors c'est de l'inconscience...
Tout comme est de la négligence de ne pas y avoir pensé disons le matin au lieu du soir 22 h...
Quand le vin est tiré, il faut le boire, dit le proverbe...

D'autant qu'écrire ça :

Celui-là, je n’en n’ai pas vraiment fait avant et je n’y arrive pas vraiment pouvez vous me le résoudre en me l’expliquant si vous le voulez bien, pour que je puisse en faire d’autre et vous les montrer merci...

C'est quoi vraiment ? On tu en as déjà fait ou  alors non...
Si tu n'en as jamais fait, alors tu n'en auras pas en contrôle, dans le cas contraire, tu es en train de te mentir...

Et c'est tellement basique (c'est une application directe du cours)...
Voyons cela point par point.

A(0;5)     B(-2;1)      C(5;4)
1) Déterminer les coordonnées du vecteur $\overrightarrow{AB}$
    Que dit ta leçon ?
    A est l'origine de ce  vecteur, B est en l'extrémité.
    Avec deux points  $A(x_A\,;\,y_A)$ et $B(x_B\,;\,y_B)$, les coordonnées du vecteur $\overrightarrow{AB}$ sont :
    $\overrightarrow{AB}(x_B-x_A\,;\,y_B-y_A)$
    Ce qui est en bon français se dit :
    (abscisse de l'extrémité - abscisse de l'origine ; ordonnée de l'extrémité - ordonnée de l'origine)
    Le calcul se fait toujours dans le sens : extrémité - origine.
    $\overrightarrow{AB}(x_B-x_A\,;\,y_B-y_A)$ d'où $\overrightarrow{AB}(-2-0\,;\,1-5)$
    Et enfin $\overrightarrow{AB}(-2\,;\,-4)$

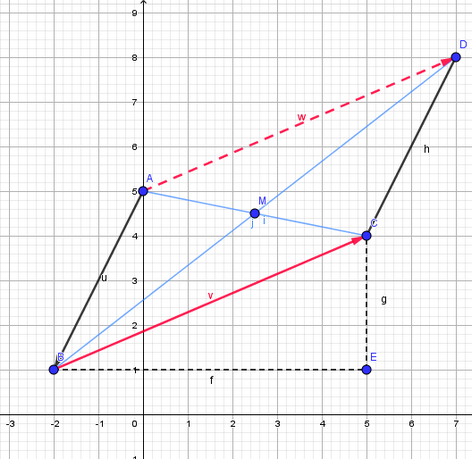
2. Déterminer les coordonnées du point D tel que ABCD soit un parallélogramme.
    Propriétés qui lient vecteurs et parallélogramme :
    Si ABCD est un parallélogramme alors  on peut écrire les égalités (entre autres) suivantes :
    * $\overrightarrow{AB} = \overrightarrow{DC}$
    * $\overrightarrow{AD} = \overrightarrow{BC}$

3. Ici, je choisis la diagonale [AC] et non [BD], pourquoi ?
    Si je calcule les coordonnées de M, milieu de [BD], ce calcul se fera à partir des cordonnées de D que je viens de calculer.
    S'il y a une erreur dans ces calculs, les coordonnées de M seront fausses aussi.
    Mais les coordonnées de A et C sont forcément justes : elles sont dans l'énoncé.
    Donc il y a un risque d'erreur en moins...
    Calcul des coordonnées du centre M du parallélogramme ABCD en utilisant la diagonale [AC]
   
    Si l'une des égalités suivantes est vérifiée :
    * $\overrightarrow{AB} = \overrightarrow{DC}$
    * $\overrightarrow{AD} = \overrightarrow{BC}$
    alors ABCD est un parallélogramme.

    La question posée devient alors : calculer les coordonnées du point D pour que
    * $\overrightarrow{AB} = \overrightarrow{DC}$
    * $\overrightarrow{AD} = \overrightarrow{BC}$

    Supposons que je choisisse la 2e : $\overrightarrow{AD} = \overrightarrow{BC}$.
    Je ne connais pas les coordonnées de D, donc je les appelle $x$ et $y$ : $D(x\,;\,y)$
    Coordonnées du vecteur $\overrightarrow{AD}$  :  $\overrightarrow{AD}(x_D-x_A\,;\,y_D-y_A)$
    Ici : $\overrightarrow{AD}(x-0\,;\,y-5)$  soit $\overrightarrow{AD}(x\,;\,y-5)$

    Coordonnées du vecteur $\overrightarrow{BC}$  :  $\overrightarrow{BC}(x_C-x_B\,;\,y_C-y_B)$
    Ici : $\overrightarrow{BC}(5-(-2)\,;\,4-1)$  soit $\overrightarrow{BC}(7\,;\,3)$
   
     Maintenant, il te faut trouver $x$ et $y$ tel que : $\overrightarrow{AD}(x\,;\,y-5)=\overrightarrow{BC}(7\,;\,3)$
     Et il te faut résoudre ces deux équations :
     $\begin{cases}x &= 7\\y-5&=3\end{cases}$
     Pas trop dur quand même, surtout la première ^_^...
     On a donc $D(7\;;\,8)$

3. Centre du parallélogramme.
    Encore la leçon (Classe de 5e cette fois) : les diagonales d'un parallélogramme ont le même milieu.
    J'appelle M le centre du parallélogramme ABCD.
    M est le milieu de la diagonale [AC] et aussi celui de la diagonale [BD].
    Nouvel appel au cours (3e, 2nde) les coordonnées du milieu M d'un segment [AB] sont moyenne des abscisses ; moyenne des ordonnées.
    Avec $A(x_A\,;\,y_A)$ et $B(x_B\,;\,y_B)$, les coordonnées de M sont
    $M\begin{cases}x_M&=\dfrac{x_A+x_B}{2}\\ y_M&=\dfrac{y_A+y_B}{2}\end{cases}$

    Ici, je vais utiliser les coordonnées de A et C pour calculer les coordonnées du milieu de la diagonale [AC].
    Utiliser la diagonale [BD] conduirait au même résultat, sauf que les coordonnées de D viendront du calcul du 2)...
    Et en cas de coordonnées fausses celles de M le seront aussi !
    En utilisant A et C dont les coordonnées sont dans l'énoncé, on a donc un risque d'erreur en moins...
    On a $A(0\,;\,5)$ et  $C(5,\;4)$
    Donc
    $M\begin{cases}x_M&=\dfrac{x_A+x_C}{2}=\dfrac{0+5}{2}=\dfrac 5 2\\ y_M&=\dfrac{y_A+y_C}{2}=\dfrac{5+4}{2}=\dfrac 9 2\end{cases}$

@+

---

Arx Tarpeia Capitoli proxima...