Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#26 20-08-2019 18:43:22
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Salut Yoshi, donc je trace un triangle équilatéral ?
Hors ligne
#27 20-08-2019 18:46:56
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
je suis quand même obligé d'utiliser le rapporteur pour tracer un triangle équilatéral, non ?
Hors ligne
#28 20-08-2019 19:10:38
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Rooooh...
Non !
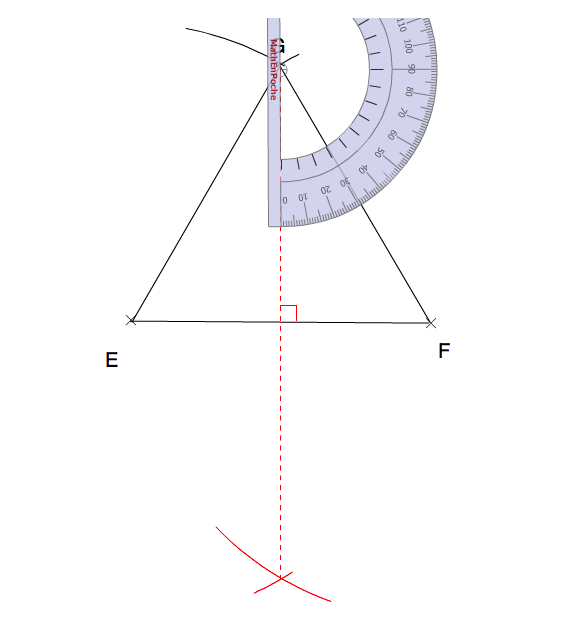
3 côtés égaux :
tu places 2 points E et F, tu traces le segment [EF].
Tu choisis une ouverture de compas égale à EF.
Pointe sur E, tu traces un arc de cercle,
Ponte sur F, tu traces un arc de cercle,
ils se recoupent : soit G le point d'intersection
On a donc contruiy EG =EF et FG = EF, on adonc EG=EF =FG : 3 côtés égaux --> triangle équilatéral.
Triangle équilatéral --> 3 angles de 60°...
Tu n'as jamais fait ça ?
Arx Tarpeia Capitoli proxima...
En ligne
#29 20-08-2019 20:13:05
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Hors ligne
#30 20-08-2019 21:00:48
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Ren
Oui, tu as tracé la bissectrice de l'angle G sachant qu'elle devait passer par G : la tâche t'a été facilitée par le fait que GE = GF...
Et MathenPoche -Sesamath, c'est très bien fait... ;-)
@+
Arx Tarpeia Capitoli proxima...
En ligne
#31 20-08-2019 21:09:17
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
oui, merci de m'avoir répondu si tard, bonne soirée …
Hors ligne
#32 21-08-2019 09:29:39
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 088
Re : Cosinus d'un angle
Bonjour,
@Yann, concernant la construction du triangle équilatéral EFG:
le segment [EF] étant tracé. On sait : EF=EG=FG, soit deux égalités :
1) EF=EG qui traduit que G et F sont à egale distance de E; soit G est sur le cercle de centre E de rayon EF
2)FG=FE qui traduit que G et E sont à égale distance de F. G est donc sur le cercle de centre F de rayon FE=EF
de 1) et 2) il résulte que G est sur l'intersection des deux cercles précités. D'où 2 possibilités pour G comme indiqué sur la figure de ton post #29, car il y a deux intersections possibles
Dernière modification par Zebulor (21-08-2019 14:21:13)
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne
#33 21-08-2019 13:29:47
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Salut Yoshi, j'ai compléter le tableau après avoir construit un triangle dont l'angle aigu est 15°
Ainsi, en changeant la longueur du segment [AB]
1. j'observe que la longueur du segment [AC] est un peu plus grande que celle du segment [AB]
2. Avec une longueur AB = 6cm, le rapport AB/AC se rapproche de la valeur de 0.9659
-
| Valeurs | Cos (15°)
| | |
| | | |
| AB | 4 cm | |
| | | |
| | | |
| AC | 4.1 cm | |
| | | |
| | | |
| AB | 0.9756 | |
| AC | | |
| | | |
| | | |
| AB | 6 cm | |
| | | |
| | | |
| AC | 6.2 cm | |
| | | |
| | | |
| AB | 0.9677 | |
| AC | | |
| | | |
| | | |
| AB | 8 cm | |
| | | |
| | | |
| AC | 8.1 cm | |
| | | |
| | | |
| AB | 0.9876 | |
| AC | | |
| | | |
Hors ligne
#34 21-08-2019 14:27:54
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 088
Re : Cosinus d'un angle
@Yann : ca paraît pas mal...
peut être que tu peux essayer d'être plus précis sur AC pour AB=8 cm.. la mesure de AC tient de la chirurgie de précision...
Dernière modification par Zebulor (21-08-2019 14:39:12)
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne
#35 21-08-2019 14:47:47
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Bonjour, j'ai construit 3 triangles avec AB = 4cm, 6cm et 8cm
mesure de [AC] = 8.1 cm pour AB d'une longueur 8cm
As tu trouvé une longueur différente ?
Hors ligne
#36 21-08-2019 14:53:08
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 088
Re : Cosinus d'un angle
Pour un angle de 15 degrés je suis plus proche de AC=8,3 cm.. Il faut une pointe de crayon très fine si on veut être précis..
Il faut voir ensuite quel est le but de la manoeuvre de ces mesures dans cet exercice, mais autant laisser Yoshi prendre le relais...
Dernière modification par Zebulor (21-08-2019 15:08:04)
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne
#37 21-08-2019 20:13:15
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Bonsoir, merci pour ton aide, ainsi j'ai corrigé la longueur de AC pour 1 angle de 15°
-
| Valeurs | Cos (15°)
| | |
| | | |
| AB | 4 cm | |
| | | |
| | | |
| AC | 4.1 cm | |
| | | |
| | | |
| AB | 0.9756 | |
| AC | | |
| | | |
| | | |
| AB | 6 cm | |
| | | |
| | | |
| AC | 6.2 cm | |
| | | |
| | | |
| AB | 0.9677 | |
| AC | | |
| | | |
| | | |
| AB | 8 cm | |
| | | |
| | | |
| AC | 8.3 cm | |
| | | |
| | | |
| AB | 0.9638 | |
| AC | | |
| | | |
pour une longueur AB = 6cm, le rapport AB/AC= 0.967 est proche de cos (15°)
pour une longueur AB = 8 cm, AB/AC = 0.9638 est proche de cos (15°)
Hors ligne
#38 21-08-2019 20:31:01
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Ok,
Donc, tu as pu constater expérimentalement que ce qu'on appelle cosinus d'un angle est le rapport (quotient) de ses 2 côtés le petit par le grand : au passage, tu peux donc en déduire que, peu importe l'angle choisi le cosinus de cet angle sera toujours inférieur ou égal à 1...
C'est bon ?
Alors, tu peux passer à un vrai exo...
Par exemple ceux dans une page où il y a des triangles dessinés et où je demande angle, côté adjacent, hypoténuse...
@zebulor
J'avais écrit p. 1 post #25 :
YannD a écrit :donc je n'ai pas besoin de calculer cos(15°) ?
Bien sûr que si ! Puisque je demandais de comparer le rapport $\dfrac{AB}{AC}$ quand l'angle vaut 60°, 45°, 30°, 15° pour chaque valeur de AB différente.
Je rappelle l'idée qui était derrière :
- travail en groupe
- chaque groupe choisissait une longueur et un angle et faisait sa construction.
- mesure de AC et calcul de AB/AC --> On note les valeurs
- on prend la calculatrice et on demande le cosinus de l'angle choisi. On note le résultat.
- lorsque tout le monde a fini : compilation des résultats...
- constat que chaque groupe a remarqué que $\cos \widehat{CAB}$ donné par la calculette est très proche de AB/AC.*Tu peux te limiter à 2 angles et une longueur AB : tu n'es qu'un seul groupe à toi tout seul...
Un exo Python instructif : http://www.bibmath.net/forums/viewtopic … 437#p78437...
@+
Arx Tarpeia Capitoli proxima...
En ligne
#39 21-08-2019 20:45:46
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Bonsoir Yoshi, pour la construction d'un triangle avec un angle de 15° : je me suis retrouvé avec un triangle qui n'est pas rectangle, j'ai pris une équerre et j'ai tracé un angle droit mais il me semble que tu m'as dit qu'il ne faut pas tracer directement à l'équerre ?
est-ce que c'est comme ça que tu demande de faire la construction .?
Hors ligne
#40 21-08-2019 21:12:16
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Re,
Oui, je l'ai dit... Elle ne sont pas fiables ou alors il faut la payer... cher !
Donc, non pas d'équerre pour une perpendiculaire.
Tu traces la perpendiculaire... au compas !
Je te l'ai déjà fait travailler l'an dernier...
Une fois tracé ton segment [AB], tu le prolonges du côté de B, en une demi-droite.
Avec une ouverture de compas égale à AB, pointe en B tu recoupes la demi-droite en un point P (nom choisi au hasard mais pas A, B ou C)
B est donc le milieu de [AP].
Au compas toujours (avec ou non l'ouverture précédente) tu construis alors la médiatrice de [AP], : passant par le milieu du segment, elle passera par B et lui sera perpendiculaire...
C'est ce qu'on souhaitait !
@+
Arx Tarpeia Capitoli proxima...
En ligne
#41 21-08-2019 21:53:06
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 088
Re : Cosinus d'un angle
Bonsoir a vous deux;
@Yoshi : ok pour le post #25! travail de groupe.... chose que je n'ai jamais fait à cet age..
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne
#42 29-08-2019 16:02:49
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Cosinus d'un angle
Bonjour Yoshi, je vais avoir beaucoup de Trigo cette année, aussi au # 38, tu me conseilles un exo où i l. y. a des triangles dessinés
Peux-tu m'orienter ? (s'il te plait )
j'ai regardé la page HOW TO mais l'exercice est déjà corrigé . . .
Hors ligne
#43 29-08-2019 18:24:00
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Salut,
Le HOW TO est une aide montrant ce que tu dois faire ...
Les exercices qui suivent ne sont corrigés qu'à la fin.
Le 1er de ces exos avec triangles dessinés, si on parle bien de la même pages
est un triangle ABC rectangle en B avec BC=3 et AC=8
Je demande la valeur de l'angle C...
A quoi sert ce HowTo si devant lui tu ressembles à une poule qui aurait trouvé un couteau comme disait mon père.
Secoue-toi et ne fais pas de misérabilisme !
Le HowTo c'est des questions Comment faire ceci, comment faire cela ?
Question 1
Comment trouver la valeur d'un angle aigu ?
On est bien dans ce cas, non ?
La fonction dont tu vas avoir besoin c'est la deuxième fonction de la touche Cos, Sin ou Tan.
1. Tu as besoin de connaître la valeur du Cos de l'angle ou la valeur du Sin de l'angle ou la valeur de la Tan de l'angle...
2. Comment choisir ?
3. A cette question on répond par une autre : comment sont placés les côtés qu'on te donne par rapport à l'angle ?
a) J'ai l'hypoténuse : alors on peut éliminer la Tangente
Comment est placé l'autre côté ?
$\alpha$) côté adjacent (le 2e côté de l'angle) ---> Cosinus
$\beta$) côté opposé (celui qui est en face) ---> Sinus
b) Je n'ai pas l'hypoténuse : on élimine Sin et Cos, donc on utilise la Tangente.
Le 1er exo proposé te place dans quel cas ? 3)a)$\alpha$) -- 3)a)$\beta$) ou 3)b) ?
Il n'y a pas d'autre solution !
C'est bien conforme à ce qui est écrit dans question 1 ?
Alors tu dois connaître les 3 définitions :
sinus = opposé/hypoténuse
cosinus = adjacent/hypoténuse
tangente = opposé/adjacent
je vais appeler division le quotient à faire.
Donc avec ta calculatrice tu tapes : 2e fonction de Sin, Cos ou Tan(division) = (ou EXE) ça dépend des machines.
Ta calculette peut fonctionner en degrés en radians (ou même en grades il me semble).
Pour tous ces exos, choisis comme unité d'angle le degré...
Allez, au taf !
@+
Arx Tarpeia Capitoli proxima...
En ligne
#44 03-09-2019 00:44:41
- ishoulita
- Membre
- Inscription : 02-09-2019
- Messages : 13
Re : Cosinus d'un angle
Salut , mais la formule cos (a+b) je t'assure que je n'ai pas encore vu, là, j'ai regardé le cours , on a fait le chapitre il y a 4 mois , je vois rien sur cos(a+b)
https://audacity.onl/ l'angle est construit au compas, d'accord mais comment je construis un angle de 15° avec le compas?
- > franchement, je vois plus comment on fait…
et sous la main je n'ai pas de rapporteur, donc je suis obligé https://mails.tips/temp-mail/de faire au compas pour avoir des valeurs de https://origin.onl/AC. Peux-tu m'aider , s'il te plait ?
L'objectif est de mettre en évidence le lien qui existe entre la valeur de l'angle aigu
Dernière modification par ishoulita (04-09-2019 21:54:59)
Hors ligne
#45 03-09-2019 10:12:56
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 985
Re : Cosinus d'un angle
Bonjour,
@Ishoulta
L'objectif est de mettre en évidence le lien qui existe entre la valeur de l'angle aigu
Entre la valeur de l'angle aigu et ... ?
Si c'est ... le cosinus de l'angle, alors tu "enfonces une porte ouverte" !
Bien sûr qu'il y a un rapport entre la valeur de l'angle aigu et son cosinus : le cosi,us d'un angle, dépend de la valeur de l'angle : quelle découverte !
Non, plus sérieusement, post #38 j'ai écrit :
- constat que chaque groupe a remarqué que $cos\widehat{CAB}$ donné par la calculette est très proche de AB/AC
.
Le lien qu'il s'agissait de remarquer était entre la valeur de l'angle et le quotient des longueurs de ses côtés et que la calculette connaissant la valeur de l'angle donnait ce quotient en utilisant la touche cos, abréviation de cosinus...
Et donc, en quoi réponds au texte que tu encadré ?
@+
Arx Tarpeia Capitoli proxima...
En ligne