Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 08-08-2019 15:46:50
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Dm commun 2de
Salut Yoshi,
Tu m'as proposé un DM 2h de seconde, j'ai fait le 1er exo
(je l'ai d'abord fait sur papier en 40min mais pour tout recopier sur internet j'ai mis 1 peu plus de temps
ANALYSE
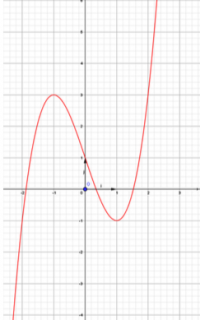
Soit f la fonction définie pour tout réel x par f(x) = x(au cube ) -3x + 1 et C sa courbe représentative donnée ci-contre
1. Calculer les images par f de 3/2; -2 et √3
(On donnera les valeurs exactes)
2. Déterminer graphiquement, en justifiant les antécédents de 3.
3. D'après la courbe, dresser le tableau de variations de la fonction
4. À l'aide de la question précédente, est-il possible de comparer
a) $f(-1.3)$ et $f(-1.25)$
b) $f(-0.2)$ et $f(0.3)$
c) $f(-0.7)$ et $f(1.3)$
5. Développer $(x-1)² (x+2)$
En déduire une factorisation de $f(x) + 1$, puis résoudre l'équation $f(x) + 1 = 0.$
6. Résoudre par le calcul
a) l'équation $f(x) = 1$
b) l'équation $f(x) < 1$
7. En justifiant avec les résultats de la question 6, dire si ce point de la courbe -1.7 a une ordonnée supérieure à 1 ou pas.
1. Calculer les images par f de :
f(3/2) = (3/2)(au cube) - 3(3/2) + 1 = (27 / 8) - (9/2) + 1 = (27/8) - (36/8) + (8/8) = (-9/8) + (8/8) = (-1/8) = - 0.125
f(-2) = (-2) (au cube) - 3(-2) + 1. = - 8 + 6 + 1 = -2+1 = -1
f(√3) = (√3)(au cube) - 3 (√3) + 1
2. Déterminer graphiquement , en justifiant, les antécédents de 3.
Les antécédents de 3 sont tous les points ayant pour ordonnée 3.
En traçant la droite y = 3
je peux Lire sur le graphique les abscisses des points x = -1 et x = 2
3. D'après la courbe, dresser le tableau de vaariation de la fonction f
f(-1.9) = 0
f(-1) = 3
f((1) = -1
x |-∞ -1.9 -1 0.35 1 |+∞
------- |------------------| -------------|------------------|--------------- |------------|
| | | |
f(x). | - 0 + 3 + 0 - -1 +. |
| | | |
--------|--------------- - -|--------------|------------------|---------------| -----------|
flèche flèche flèche flèche flèche vers
vers le haut vers le haut vers le bas vers le bas le haut
4. A l'aide de la question précédente est-il possible de comparer :
a ) $f(-1.3)$ et $f(-1.25)$
oui, il est possible de comparer f(-1.3) et f(-1.25) parce que dans cet intervalle
f est croissante donc d'après la définition de la fonction croissante, les images sont rangées
dans le même ordre que les antécédents - 1.3 < -1.25 donc f(-1.3) < f(-1.25)
b) $f(-0.2)$ et $f(0.3)$
les valeurs -0.2 et 0.3 sont dans l'intervalle ]-1;0.35[ du tableau et pour cet intervalle
f(x) est décroissante
donc d'après la définition de la fonction décroissante les images sont rangées dans l'ordre inverse des antécédents
comme -0.2 < 0.3 alors f(-0.2) > f(0.3)
c ) $f(-0.7)$ et $(1.3)$
oui, il est possible de comparer f(-0.2) et f(0.3) puisque dans cet intervalle f(x) >
5. Développer $(x-1)²(x+2)$
(x-1)² (x+2)
= (x² - 2x + 1) (x+2)
= x(au cube) - 2x² + x + 2x² -4x + 2
= x(au cube) -3x + 2
En déduire une factorisation de $f(x) + 1$ ,
f(x) = x(au cube) -3x + 1
et x(au cube) - 3x + 2 peut aussi s'écrire [x(au cube) -3x + 1 ]+ 1
donc x(au cube) - 3x + 2 = f(x) + 1
Résoudre $f(x)+1 = 0$.
f(x) + 1 = 0 <=> (x-1)²(x+2) = 0 <=> (x-1)(x-1)(x+2)= 0
6. Résoudre par le calcul
a) l'équation f(x) = 1
x(au cube) -3x + 1 = 1 <=> x(au cube) - 3x + 1 - 1 = 0 <=> x(au cube) - 3x = 0 <=> x(x²-3) = 0 <=> x = 0 ou
x²-3 = 0
je cherche les solutions de x²-3
x²-3 = 0 <=> (x - √3) (x +√3) = 0 <=> x - √3 = 0 ou bien x +√3 = 0
les solutions de l'équation x²-3 = 0 sont -√3 et √3
b) l'inéquation f(x) < 1
x(au cube) - 3x + 1 < 1 <=> x(au cube) - 3x +1 - 1 < 0 <=> x(au cube) - 3x < 0 <=> x(x²-3) < 0
x |-∞ - √3 0. √3 |+∞
x | - - 0 + + |
---------|-------------|----------------|------------|-----------|
x + √3. | - 0 + | + | + |
---------|-------------|-----------—— |------------|---------- |
x - √3 | - | - | - 0 + |
---------|-------------|----------------|------------|-----------|
| + | + | - | +
7. En justifiant avec les résultats de la question 6, dire si le point de la courbe d'abscisse -1.7 a une ordonnée
supérieure à 1
J'ai mis oui, parce que d'après la 1ere colonne du tableau je trouve un + et -√3 < 1.7
Dernière modification par yannD (08-08-2019 17:06:38)
Hors ligne
#2 08-08-2019 16:10:49
- Volesprit
- Membre
- Inscription : 08-08-2019
- Messages : 9
Re : Dm commun 2de
Bonjour,
pour le 1) : (√3)^3 se simplifie, piste : un nombre au cube est un nombre au carré fois lui même.
Bonne fin de journée
Hors ligne
#3 08-08-2019 16:18:24
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
√3 ^3 = (√3)² x √3
Hors ligne
#4 08-08-2019 16:35:20
- Volesprit
- Membre
- Inscription : 08-08-2019
- Messages : 9
Re : Dm commun 2de
(√3)²=? et donc f(√3)=?
Dernière modification par Volesprit (08-08-2019 16:36:48)
Hors ligne
#5 08-08-2019 16:42:36
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
(√3)² = 3 donc f(√3) = (√3)² x √3 = 3√3
Hors ligne
#6 08-08-2019 16:44:26
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
non f(√3) = (√3)² x √3 -3x(√3) + 1 = 3√3 - 3√3 + 1
donc c'est 1
Hors ligne
#7 08-08-2019 16:51:13
- Volesprit
- Membre
- Inscription : 08-08-2019
- Messages : 9
Re : Dm commun 2de
non f(√3) = (√3)² x √3 -3x(√3) + 1 = 3√3 - 3√3 + 1
donc c'est 1
Bingo!
Hors ligne
#8 08-08-2019 17:02:07
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
√3 = 1.73 et l'ordonnée est bien 1 sur le graphique
Hors ligne
#9 08-08-2019 17:04:26
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
pour la 3. j'ai fait un tableau de variation mais je ne sais pas si celui-ci est correct ?
pouvez -vous m'aidez , s'il vous plait ?
Hors ligne
#10 08-08-2019 17:16:38
- Volesprit
- Membre
- Inscription : 08-08-2019
- Messages : 9
Re : Dm commun 2de
Si c'est un tableau de variations les signes sont superflus, mais effectivement graphiquement la courbe à l'aire croissante jusqu'en -1 puis décroissante jusqu'en 1 pour redevenir croissante, les extremums que tu as indiqués semblent bons en -1 et en 1 mais les autres valeurs ne sont pas demandées
Hors ligne
#11 08-08-2019 17:33:05
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
les autres valeurs ne sont pas demandées. D'accord
coté gauche : je vois que f(x) < 0 donc je dois chercher sur le graphique l'abscisse du point de la courbe qui coupe l'axe des x, ce n'est pas ça ?
Hors ligne
#12 08-08-2019 18:12:32
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Dm commun 2de
Bonjour,
Erreur 1ere colonne de signe tableau 6b, je le reprends chez toi et j'ajoute une séparation horizontale :
x |-∞ - √3 0. √3 +∞|
---------|-------------|----------------|------------|-----------|
x | - | - 0 + + |
---------|-------------|----------------|------------|-----------|
x + √3. | - 0 + | + | + |
---------|-------------|-----------—— |------------|---------- |
x - √3 | - | - | - 0 + |
---------|-------------|----------------|------------|-----------|
| + | + | - | + |
Moyennant quoi tu vois que pour x <-3 :
signe de x : -
signe de $x+\sqrt 3$ : -
signe de $x -\sqrt 3$ : -
Et que donc pour x <-3 le signe de $(x+\sqrt 3)(x-\sqrt 3)$ est $- \times - \times -$ qui ne donne pas +
Question 3.
Volesprit a souligné un point important et j'en rajoute une couche.
Si tu regardes l'allure générale de la courbe : elle croît, décroît puis croît de nouveau
Le tableau se présente donc ainsi
x |-oo -1 1 +oo|
------|---------|---------|---------|
| ? ? |
| / \ / |
| / \ / |
f(x) | / \ / |
| / \ / |
| ? ? |
Et seuls les points d'interrogation sont à remplacer par les valeurs ou mentions adéquates...
@+
[EDIT]
coté gauche : je vois que f(x) < 0 donc je dois chercher sur le graphique l'abscisse du point de la courbe qui coupe l'axe des x, ce n'est pas ça ?
Veux-tu bien préciser ce que tu cherches à faire ?
Dernière modification par yoshi (08-08-2019 18:14:20)
Arx Tarpeia Capitoli proxima...
Hors ligne
#13 08-08-2019 18:52:27
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Hors ligne
#14 08-08-2019 18:57:59
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
la partie en dessous de l'axe des x : f(x) est bien < 0,
et la partie au dessus de l'axe des x : f(x) est bien > 0
est-ce que c'est ça ?
Hors ligne
#15 08-08-2019 19:35:18
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
pour le tableau de variation; j'ai du mal comprendre en cours que c'est l'allure de la courbe et pas le signe de f(x)
je pense que c'est ça
parce que ce matin , quand j'ai fait le DM, j'ai cherché l'abscisse du point de la courbe qui coupe l'axe des x
Hors ligne
#16 08-08-2019 20:12:53
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Dm commun 2de
Re,
la partie en dessous de l'axe des x : f(x) est bien < 0,
et la partie au dessus de l'axe des x : f(x) est bien > 0
est-ce que c'est ça ?
Oui, mais dans ce DM, c'était hors-sujet...
Quand on parle de sens de variation d'une fonction, on cherche croissance, décroissance extrema éventuels, "limites" (avec des guillemets... parce qu'en seconde, l'étendue des limites possibles est assez... limitée ! ^_^)
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#17 08-08-2019 20:20:12
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
Bonsoir Yoshi, quelle note aurais tu donné ?
est ce que la question 4 est bien rédigée parce que à ce type de question, je me suis parfois trompé (en fin disons que je fais des phrases qui ne sont pas très précise…
Dernière modification par yannD (08-08-2019 20:24:32)
Hors ligne
#18 08-08-2019 20:24:53
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Dm commun 2de
je voulais parler de la question 4, est ce que cela te parait oK
As-tu une autre formulation plus "chouette "
Dernière modification par yannD (08-08-2019 20:26:06)
Hors ligne
Pages : 1
Discussion fermée