Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#76 20-06-2019 17:09:00
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
RE,
Et dernière propriété :
Citation incorrecte : il manque un élément essentiel qui la rend fausse :
une droite qui passe par le milieu d'un seul côté parallèlement à 2e côté, coupe l'autre le 3e côté en son milieu.
Ensuite dans le chapitre Triangle rectangle et cercle, et bien on n' a pas parlé de demi-cercle...
C'est normal, ne sois pas surpris : cela fait plus de 30 ans que je n'ai plus vu cette définition dans le chapitre concerné...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#77 20-06-2019 18:27:08
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
j'ai essayé d'appliquer la définition du # 74 mais je ne vois pas comment tu en déduis les 2 autres définitions
Peux-tu m'expliquer s'il te plait ?
Hors ligne
#78 20-06-2019 20:29:44
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
Re,
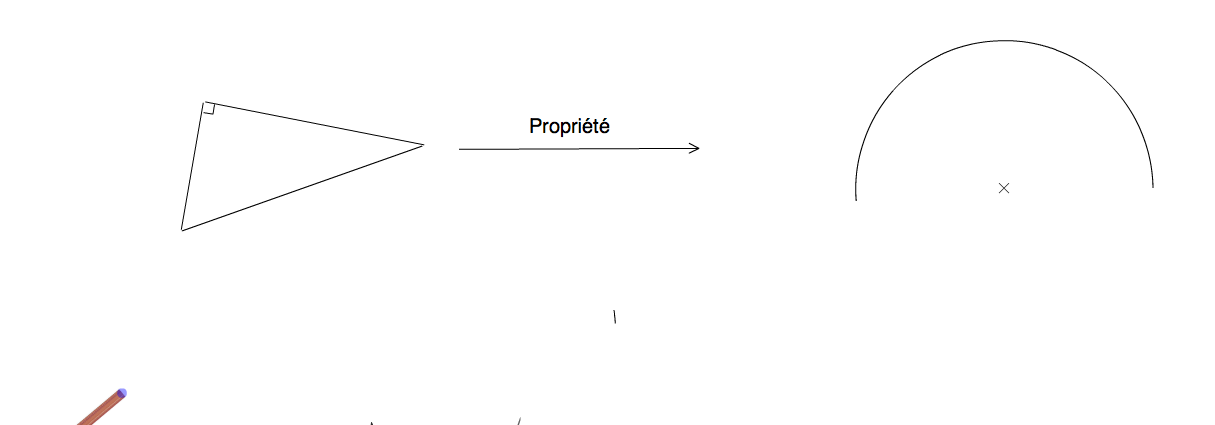
Tout triangle rectangle est inscriptible dans un demi-cercle.
Tu prends [BC] hypoténuse et A l'angle droit..
Ya plein de solutions...
Tu prends I milieu de [BC].
1. [AI] médiane relative à l'hypoténuse, donc IA = IB =IC donc un cercle de centre de I est circonscrit au triangle ABC.
Ce cercle a pour diamètre [BC], puisque son centre I en est le milieu.
Et comme A est sur le cercle, d'après la définition il est contenu dans un demi-cercle...
2. a) On sait que les 3 médiatrices se coupent en I milieu de [BC]. Donc d'après la propriété du point d'une médiatrice :
IA = IB = IC. Et on a donc un cercle de centre OI et de rayon IA = IB = IC... Voir ci-dessus...
b) Mieux : on sait que le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse... Donc, voir 1.
c) On ne sait pas tout ça... OK ! Alors, on le redémontre. Soit I le milieu de l'hypoténuse [BC].
La perp. à (AB) passant par I coupe (AB) en H. La perp. à (AC) passant par I coupe (AC) en K.
$ (IH) \perp (AB)$
$(AC) \perp (AB)$ ($\hat A$ est droit)
Conclusion : $(IH) // (AC).
Or, dans le tr. ABC la droite passe par le milieu du côté [BC] parallèlement au côté (AC), coupe le 3e côté [AB] en son milieu.
H est donc le milieu de [AB]. Donc (IH) médiatrice de [AB]. Donc IA = IB.
On montrerait de même que (IK) médiatrice de [AC]. Donc IA = IC.
Donc IA = IB = IC. Voir 1.
3. Tu construis D symétrique de par rapport à I. Et tu montres que BACD est un rectangle ==> Diagonales [AD] et [BC] même longueur.
AD = BC. I milieu de [AB] et [BC], d'où IB = IA = IC = ID. Tu gardes IB = IA = UC. Voir 1.
..........................
2. Réciproque.
Le triangle ABC est dans un demi-cercle. Supposons que le plus grand côté s'appelle [BC]. [BC] est un diamètre de ce demi-cercle.
a) L'angle $\widehat{BAC}$ est un angle inscrit qui intercepte l'arc BC. Cet arc est aussi intercepté par l'angle au centre $\widehat{BIC}$
L'angle inscrit vaut la moitié de l'angle au centre qui intercepte le même arc. $\widehat{BIC}$ est un angle plat et mesure 180°.
Donc $\widehat{BAC}=90^\circ$. BAC est un triangle rectangle en A.
b) A, B, C sur le cercle de diamètre [BC] et de centre I milieu de [BC]. D'où IB = IA = IC rayon.
* Tu connais la réciproque.
Si dans un triangle la médiane relative au plus grand côté vaut la moitié de ce côté, alors ce triangle est
rectangle d'hypoténuse ce plus grand côté.
* Tu ne la connais pas.
Alors on part sur des calculs d'angles.
IA = IB donc AIB isocèle. Donc $\widehat{IBA} =\widehat{IAB}$
IA = IC donc AIC isocèle. Donc $\widehat{ICA} =\widehat{IAC}$
Faisons la somme : $\widehat{IBA} +(\widehat{IAB}+\widehat{IAC})+\widehat{ICA}=\widehat{IBA} +\widehat{BAC}+\widehat{ICA}=180^\circ$ (somme des angles d'un
triangle)
Mais $\widehat{IBA} +\widehat{IAB}+\widehat{IAC})+\widehat{ICA}=2\widehat{IAB}+2\widehat{IAC}=2(\widehat{IAB}+\widehat{IAC}=2\widehat{BAC}=180^\circ$
Donc $\widehat{BAC}=90^\circ$ Donc BAC rectangle en A ?
Stop ou encore ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#79 20-06-2019 21:15:28
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
disons Stop
mais ce que je voulais savoir c'est surtout pourquoi avant on disait qu'un triangle est inscrit dans un demi-cercle si l'un de ses sommets est sur le cercle et les 2 autres représentent un diamètre
dans mon cours c'est avec un cercle et là dans le # 74 tu parles d'un demi-cercle
Hors ligne
#80 20-06-2019 21:16:53
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
tu dit que c'est bien plus précis mais pourquoi c'est plus précis de prendre le demi-cercle
Hors ligne
#81 20-06-2019 21:23:21
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Hors ligne
#82 21-06-2019 15:07:47
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
Bonjour,
tu dis que c'est bien plus précis mais pourquoi c'est plus précis de prendre le demi-cercle ?
Lis et réfléchis :
* On dit qu'un triangle est inscrit dans un cercle si ses 3 sommets sont sur le cercle.
* On dit qu'un triangle est inscrit dans un demi-cercle, si l'un des sommets est sur le cercle et que les 2 autres constituent les extrémités d'un diamètre....Ne trouves-tu pas de différences ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#83 21-06-2019 15:12:27
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
Salut Yoshi, j'espère ne pas te faire trop perdre ton temps . . . mais j'ai un mal fou pour comprendre
et je retrouve les difficultés d'il y a 2 ans
Hors ligne
#84 21-06-2019 15:16:03
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
dans le 1er cas, on a 1 cercle
dans le 2e , c'est un demi-cercle
Hors ligne
#85 21-06-2019 15:47:15
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Montrer que les 3 hauteurs d'un triangle se coupent en un même point
Bin alors, c'est tout ce que tu vois comme différence ? tu n'as jamais appris à comparer deux textes ?
cercle et demi-cercle c'est une évidence.
Tu ne vois pas ce que ça entraîne comme précision dans l'un et pas dans l'autre de dire :
ABC est inscrit dans un demi-cercle
ou
ABC est inscrit dans un cercle ?
Relis les définitions...
J'ai toujours bassiné mes zèbres en leur serinant année après année : en mathématique, il y a 3 verbes absolument indispensables à connaître et utiliser dans l'ordre : observer, comparer et déduire...
Arx Tarpeia Capitoli proxima...
Hors ligne