théorème thales ou produit scalaire

PROBLEME OUVERT · 02-05-2019 22:17:12

Bonsoir un petit problème ouvert auquel je suis encore bloquée, y aurait-il quelqu'un pour m'aider s'il vous plaît ? sachant que c'est pour demain, j'ai trouvé deux méthodes; le théorème de Thalès (je bug là-dessus mais je préfère utiliser cette méthode) ou alors le produit scalaire ( je suis vraiment nul pour ce dernier...)

donc voilà l'énoncé :

ABC est un triangle rectangle en A . I est le milieu de [BC].

M est un point quelconque du segment [BC]. On projette

orthogonalement M en H sur (AB) et en K sur (AC).

Où placer le point M sur [BC] pour que (AI) et (HK) soient

perpendiculaires ?

voilà, merci d'avance ! (je suis désolé, mais je n'arrive pas à téléverser l'image de la figure dans le message, du coup voici le lien
file:///C:/Users/Sheryne_PC/Downloads/9cb8959241ab306ed7463b21fc26f0f8%20(2).pdf

yoshi · 03-05-2019 10:00:31

Bonjour,

Ne vois-tu pas dans le début de ce lien C:/Users/Sheryne_PC/ qu'il pointe vers TA machine et que personne - en principe - ne peut y accéder de l'extérieur (et heureusement !) ?
Donc
* tu te connectes à https://www.cjoint.com
* tu cliques sur Parcourir
* tu parcours ton dossier C:/Users/Sheryne_PC jusqu'à trouver le document pdf concerné
* tu cliques bouton gauche une fois dessus puis sur ouvrir
* de retour dans Cjoint, tu choisis la durée pendant laquelle le lien sera valable 4 jours, 21 jours, illimité
* tu cliques ensuite sur Créer le lien Cjoint
* tu copies le lien obtenu et tu le donnes dans ta réponse

Pour en revenir l'exercice, sauf si tu as la longueur des côtés du triangle, je doute que ton prof attende de toi des calculs...
As-tu des valeurs chiffrées pour les longueurs des côtés ?
Tu t'imagines poser BC =a, AB=c et AC = b, prendre un système d'axes orthonormés d'origine B et dont l'axe des abscisses est (BC) (de sens positif de B vers C).
Les coordonnées de B sont (0 ; 0), celles de C(a ; 0), celles de A(a/c ; bc/a) celles de I(a/2 ; 0), choisir M($x$ ; 0), en déduire les coordonnées de H et K, puis celles du vecteur $\overrightarrow{HK}$..
Enfin écrire que $\overrightarrow{HK}.\overrightarrow{AI}=0$.
Et même si tu attrrives au bout sans erreurs, je ne vois pas - a priori - en quoi cela va t'aider à placer le point M.

Je vais essayer mais je pense plutôt qu'il faut trouver une méthode de construction géométrique du point M (c'est ce qu'il faut faire quand on nous donne un problème du type appelé "problème ouvert" !)...

@+

yoshi · 03-05-2019 18:25:13

RE,

Pas de nouvelles ?
Poster le 02/05 à 22 h pour un devoir à rendre le 03/05, ça de de la prévoyance !!!...
J'espérais vaguement des indications chiffrées dans le pdf. On va faire sans... Et dans ce cas pour simplifier les calculs, je prends l'origine en A les axes des abscisses et des ordonnées sur (AB) et (AC).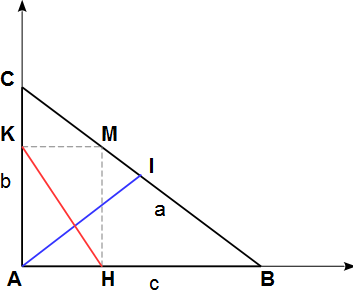

Je vais utiliser le fait que coeff. directeur(AI) x coeff. directeur(HK)=-1 (c'est du cours).
Selon l'habitude, je note BC = a, AB = c et AC = b.

J'ai donc les coordonnées suivantes :
A(0 ; 0) B(c ; 0) C(0 ; b) I(b/2 ; c/2)
Le coefficient directeur de (AI) est donc $\dfrac{\dfrac b 2}{\dfrac c 2}=\dfrac b c$
L'équation réduite de (BC) est $y=-\dfrac b c x+ b$
Soit $m$ l'abscisse de M, son ordonnée est $y=-\dfrac b c m+ b=-\dfrac{mb}{c}+b=\dfrac{-mb+bc}{c}$
$M\left(m\,;\;\dfrac{-mb+bc}{c}\right)$

On a donc $H(m\,;\,0)$ et $K\left(0\,;\,\dfrac{-mb+bc}{c}\right)$. Le coeff dir de (HK) est donc $\dfrac{\dfrac{mb-bc}{c}}{m}=\dfrac{mb-bc}{mc}$
Si coeff1 * coeff2 =-1 alors coeff1=-1/coeff2
J'écris donc :
$\dfrac{mb-bc}{mc}=-\dfrac c b\; \Leftrightarrow\;\dfrac b c \times \dfrac{m-c}{m}=-\dfrac c b\; \Leftrightarrow\;\dfrac{m-c}{m}=-\dfrac{c^2}{b^2}$
$\Leftrightarrow$
$m-c=-m\dfrac{c^2}{b^2}$
$\Leftrightarrow$
$m+m\dfrac{c^2}{b^2}=c$
$\Leftrightarrow$
$m\left(1+\dfrac{c^2}{b^2}\right)=c$

$\Leftrightarrow\;m\left(\dfrac{b^2+c^2}{b^2}\right)=c\;\Leftrightarrow\;m\times\dfrac{a^2}{b^2}=c$
Et $m= \dfrac{cb^2}{a^2}$
---------------------------------------------------------------------------------
Si je prends un triangle rectangle isocèle : $b^2=c^2=\dfrac{a^2}{2}$
d'où $m =\dfrac c 2$
Le point M de [BC] est le milieu de [BC] : M est confondu avec I.
C'est juste.

@+

yoshi · 03-05-2019 21:41:14

Re,

Je pense avoir trouvé plus simple niveau calculs...
Je pars de la droite (Ai) son coefficient directeur est $\dfrac b c$
Je prends un point H de [AB] tel que $x_H=m$
Je trace la perpendiculaire a (AI) passant par H : elle coupe [AC) en K : le coefficient directeur de (HK) est $-\dfrac c b$
L'équation de (HK) s'écrit $y=-\dfrac c b x + p$ où est p est l'ordonnée à l'origine, soit l'ordonnée de K
J'écris que cette droite passe par H : $0=-\dfrac c b \times m + p$ d'où $p=\dfrac c b \times m$
Maintenant, je trace la perpendiculaire en H à (AB) et la perpendiculaire en K à (AC) : elles se coupent en un point M de coordonnées :
$M\left(m\,;\,\dfrac c b m\right)$

J'écris alors que M sur (BC) et que donc ses coordonnées vérifient l'équation de la droite (BC).
L'équation de la droite (BC) est :
$y=-\dfrac b c x+b$
Donc :
$\dfrac c b m =-\dfrac b c m+b$
$\Leftrightarrow$
$\dfrac c b m +\dfrac b c m=b$
$\Leftrightarrow$
$m\left(\dfrac c b +\dfrac b c\right)=b$
$\Leftrightarrow$
$m\times \dfrac{c^2+b^2}{bc}=b$ en vertu du théorème de Pythagore : $c^2+b^2=a^2$ d'où $m\times \dfrac{a^2}{bc}=b$
Et enfin :
$m=b\times \dfrac{bc}{a^2}=\dfrac{b^2c}{a^2}$

@+

[EDIT] Cela dit, j'ai travaillé pour rien (enfin, si, pour moi !) parce que la miss
- n'a pas eu la correction de revenir donner de ses nouvelles
- a demandé (et probablement obtenu, ceci explique cela...) des réponses ailleurs ce qui, à mes yeux, est tout aussi incorrect !

Tout une éducation à refaire...

Dernière modification par yoshi (03-05-2019 21:46:04)

Deugard · 04-05-2019 04:43:19

bonsoir,

je donne un résultat qui est cohérent avec le précédent; en utilisant les mêmes notations, j'obtiens :
$\ CM=\dfrac{b^2}{a}$ .
1°) Dans un premier temps, je montre que le point M est en fait la projection orthogonale de A sur (BC) .
(Je passe les raisonnements : simples mais longs).
2°) J'applique ensuite un résultat classique sur le triangle rectangle qui est : "le rapport des carrés des
côtés de l'angle droit est égal au rapport de leurs projections sur l'hypoténuse" , ce qui s'écrit ici :
$\dfrac{b^2}{c^2}=\dfrac{CM}{BM}\,\,\,\,\Rightarrow \,\dfrac{b^2}{c^2}=\dfrac{CM}{a-CM}\,\,\,\Rightarrow\,\,\,b^2(a- CM)=c^2CM\,\,\,\Rightarrow\,\,\,\ CM(b^2+c^2)=ab^2\,\,\,\Rightarrow\,\,\,CM=\dfrac{ab^2}{b^2+c^2}$;
sachant que $b^2+c^2=a^2$ , j'en déduit le résultat .
3°) Je retrouve le résultat précédent de Yoshi en remarquant que les triangles ABC et KMC sont semblables ,
d'où les rapports : $\dfrac{m}{CM}=\dfrac{c}{a}\,\,\Rightarrow\,\,m=\dfrac{c}{a}.\dfrac{b^2}{a}=\dfrac{cb^2}{a^2}$ .

Dernière modification par Deugard (04-05-2019 05:24:12)

yoshi · 04-05-2019 07:30:02

Bonjour,

Une idée m'est venue de construction géométrique : ça me chagrinait de ne pas l'avoir trouvée...

Sur [AC) je place (au compas) B' tel que AB' = AB
Sur [AB), je place (au compas) le point C' tel que AC' = AC.
Je construis alors le point D tel que AB'DC' soit un rectangle.
L'intersection de [AD) et [BC] est le point M cherché.

Pourquoi ?
Ma 2e méthode m'avait conduit à un tout petit calcul qui ne m'avait pas servi pour établir le résultat...
Dans mon lit (!), hier soir, grâce à ce calcul, j'ai trouvé ladite méthode purement géométrique : j'expliciterai ça plus tard pour les curieux.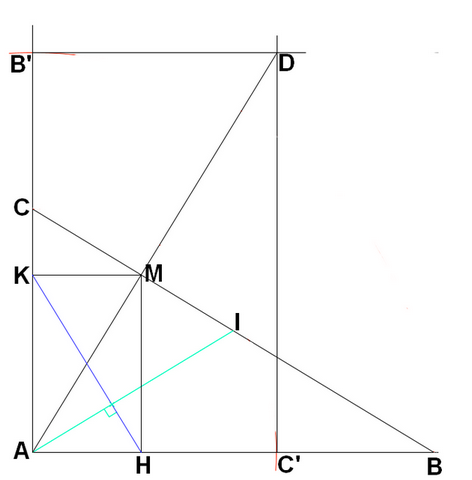

@+

[EDIT]
Les coordonnées de M au post #4, avant d'utiliser $M \in (BC)$ m'ont suffi :
J'avais abouti à
$M\left(m\,;\,\dfrac c b m\right)$
en posant
$\begin{cases}x&= m\\y&= \dfrac c b m\end{cases}$
et en remplaçant $m$ par $x $, on montre que lorsque H parcourt [AB], M parcourt la droite d'équation $y=\dfrac c b x$
L'idée est donc venue de construire D tel que $\tan(\widehat{HAD})= \dfrac c b$

Mais je ne suis que moyennement satisfait : je n'ai pas de justification géométrique pure qui me permette de me passer des calculs préalables...
Je cherche...
Si quelqu'un a l'idée avant moi, je prends !

Dernière modification par yoshi (04-05-2019 10:29:29)

yoshi · 04-05-2019 12:12:10

RE,

Je ne m'étais même pas aperçu du résultat n° 1 de Deugard : dans ce cas, c'est encore plus simple puisque A est le pied de la hauteur issue de relative à l'hypoténuse [BC]...
Je tente une démonstration.
Soit E l'intersection de (AI) et (HK), et F celui des diagonales du rectangle AKMH.
Je vais évaluer $\widehat{AMB}= \widehat{AMH}+\widehat{HMB}

$\widehat{EAH}+\widehat{EHA}=90^\circ\\ \widehat{EHA}+\widehat{EHM}=90^\circ$
Donc
$\widehat{EAH}=\widehat{EHM}$
Le triangle MFH est isocèle : $(\widehat{EHM}=)\widehat{FHM}=\widehat{FMH}$
Donc
$\widehat{EAH}=\widehat{FMH}$
AIB étant isocèle : $(\widehat{EAH}=)\widehat{IAH}=\widehat{IAH}=\widehat B$
Donc
$(\widehat{FMH}=)\widehat{AMH}=\widehat{AMH}$
Mais
$\widehat B+\widehat{HMB}=90^\circ$
On a donc
$\widehat{AMH}=\widehat B$
$\widehat B+\widehat{HMB}=90^\circ$
D'où
$\widehat{AMH}+\widehat{HMB}=90^\circ$
Et $\widehat{AMB}=90^\circ$
M est donc le pied de la hauteur abaissée de A sur [CB].

@+

yoshi · 06-05-2019 13:32:53

Bonjour,

Je joins un autre dessin sur lequel je désigne les angles par des nos, cela devrait être plus facile à suivre :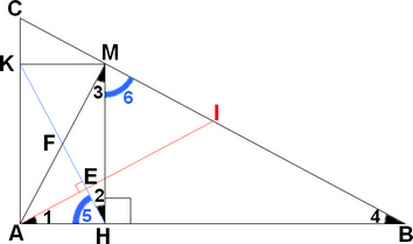

$\begin{cases}(HK)\perp (AI)\text{ donc }\hat 1 + \hat 5 &= 90^\circ\\(MH)\perp (AB)\text{ donc } \hat 2 + \hat 5 &= 90°\end{cases}$
D'où $\hat 1 = \hat 2$ comme ayant le même complément

$\begin{cases}\text{HFM tr. isocèle donc } \hat 2&= \hat 3\\ \;\;\quad\quad\quad\quad\quad\quad\quad\text{ Or, }\hat 1 &= \hat 2\end{cases}$
Donc $\hat 1 = \hat 2 =\hat 3$

$\begin{cases}\text{AIB tr. isocèle donc } \hat 1&= \hat 4\\ \;\quad\quad\quad\quad\quad\quad\quad\text{ Or, }\hat 1 &= \hat 2=\hat 3\end{cases}$
Donc $\hat 1 =\hat 2 =\hat 3 = \hat 4$

Mais le tr MHB est rectangle en H , donc $\hat 4+\hat 6=90^\circ$, et comme $\hat 3 = \hat 4$ alors $\hat 3+\hat 6=90^\circ$
$\widehat{AMB}=\hat 3+\hat 6=90^\circ$

M est donc le pied de la hauteur issue de A dans le triangle BAC.

@+

Forum de mathématiques - Bibm@th.net

#1 02-05-2019 22:17:12

théorème thales ou produit scalaire

#2 03-05-2019 10:00:31

Re : théorème thales ou produit scalaire

#3 03-05-2019 18:25:13

Re : théorème thales ou produit scalaire

#4 03-05-2019 21:41:14

Re : théorème thales ou produit scalaire

#5 04-05-2019 04:43:19

Re : théorème thales ou produit scalaire

#6 04-05-2019 07:30:02

Re : théorème thales ou produit scalaire

#7 04-05-2019 12:12:10

Re : théorème thales ou produit scalaire

#8 06-05-2019 13:32:53

Re : théorème thales ou produit scalaire

Pied de page des forums