Devoir seconde vecteur

Schéhérazade · 28-01-2019 15:42:32

Bonjour
Je bloque sur un exercice de maths 2nde .Voici l'énoncé:

On considère les points A(-2;0), B(2,0) et C ((2racine carré 5)/5 ; (4 racinecarré 5)/5) Les points C et D sont tels que ABCD est un carré et L est un demi cercle de diamètre [AB] (comme indiqué sur la figure).

Partie A
1.a)Montrer que le point C' appartient à la droite (OC).
b)calculer OC'.
c)En déduire que C' est l'intersection de (OC) et de C.

2.On considère l'homothétie h de centre O qui transforme C en C'.
a)Quel est le rapport de l'homothétie h?
b)Déterminer les coordonnées de D'=h(D).Montrer que D' appartient à L.
c)Déterminer les coordonnées de A'=h(A) et de B'=h(B).
d)Montrer que A'B'C'D' est un carré.

Partie B
3.Un triangle équilatéral IJK étant donné et en s'inspirant éventuellement des questions précédentes, construire un carré ABCD inscrit dans le triangle , c est à dire tel que: A,B appartiennent à [IJ], C appartienne à [JK] et D appartient à [IK].

On donnera les différentes étapes de la construction et on démontrera que le quadrilatère ainsi construit répond bien au problème posé.

LIEN POUR L IMAGE: https://www.e-bahut.com/topic/52819-untitled/

OU J EN SUIS:
Je n arrive pas à avancer car je bloque sur la première question:
voici ce que j'ai fait

Pour monter que C' appartient à (OC), il faut montrer que C' , O et C sont alignés, donc que les vecteurs OC' et OC sont colinéaires.Donc:
xB=2 et xA=-2 donc AB=4.ABCD est donc un carré de coté 4; soit BC=4.Comme yB=0 on a C(0;4).De plus O(0;0) et
C'((2racine carré 5)/5 ; (4 racinecarré 5)/5).
Donc vecteurOC'=((2racine carré 5)/5 ;(4 racinecarré 5)/5 ) et vecteur OC(0;4).
Pour que ces deux vecteurs soient colinéaires il faudrait que
xVecteurOC' * yVecteurOC = y Vecteur OC'*y Vecteur OC
soit (2racine carré 5)/5*4=(4 racinecarré 5)/5) * 0 .
Cet égalité est fausse donc OC' et OC ne sont pas colinéaires, donc O C et C' ne sont pas alignés et donc C' n appartient pas à (OC).Pourtant la consigne me demande de montrer que C' appartient à (OC).

Il y a donc surement une erreur dans mon raisonnement.

Un grand merci à tout ceux qui pourront m'aider car je suis vraiment bloquée et je ne peux pas continuer l'exercice à cause de cette question.

yoshi · 28-01-2019 16:20:10

Bonjour,

Heureusement que tu as su joindre ton dessin, parce que ton texte est incorrect : un petit ' oublié sur C fait toute la différence :

On considère les points A(-2;0), B(2,0) et C ((2racine carré 5)/5 ; (4 racinecarré 5)/5)

Bon, alors continuons.

D'accord pour l'ordonnée de C seule...
Mais je ne n'avais encore jamais rencontré cette formulation de la condition de colinéarité de 2 vecteurs :
[tex]xVecteurOC' * yVecteurOC = y Vecteur OC'*y Vecteur OC[/tex]
(Que signifie xVecteurOC' ?)
Mais plutôt celle-ci :
Etant donné 2 vecteurs [tex]\vec u[/tex] et [tex]\vec v[/tex] de ton repère, ces deux vecteurs sont colinéraires si et seulement s'il existe un réel k tel que [tex]\vec u = k.\vec v[/tex]
Tu ne dis pas ce que sont x et y dans ta démonstration...
Par contre : [tex]\overrightarrow{OC} (2\,;\,4)[/tex] et [tex]\overrightarrow{OC'} \left(\dfrac{2\sqrt 5}{5}\,;\,\dfrac{4\sqrt 5}{5}\right)[/tex]
Donc la faute est là et pas dans le raisonnement :

vecteur OC(0;4).

Si tu avais tracé [tex]\overrightarrow{OC}[/tex] sur ton dessin, tu l'aurais vu tout de suite...

Maintenant tu peux poursuivre et revenir si nécessaire... ^_^

@+

[EDIT] Probablement est-ce cela que tu voulais écrire : Soient [tex]\vec u(x\,;\,y)[/tex] et [tex]\vec v(x'\,;\,y')[/tex], [tex]\vec u[/tex] et [tex] \vec v[/tex] sont colinéaires ssi [tex]xy'-x'y=0[/tex].
Alors là, oui, c'est une méthode correcte, fréquente avec les coordonnées, plus simple que de rechercher le k.
Si [tex]\vec u = k.\vec v[/tex] alors en remplaçant x et y
$x= kx'$ et $y = ky'$ D'où $xy'-x'y = kx'y'-kx'y'= 0$

Dernière modification par yoshi (29-01-2019 09:36:31)

Black Jack · 28-01-2019 20:14:38

Bonjour,

Tu écris :

xB=2 et xA=-2 donc AB=4.ABCD est donc un carré de coté 4; soit BC=4.Comme yB=0 on a C(0;4)

Et bien je ne suis pas d'accord avec l'abscisse de C que tu as trouvé.

yoshi · 29-01-2019 09:23:47

Bonjour,

yoshi a écrit :

Schéhérazade a écrit :
vecteur OC(0;4).
Si tu avais tracé [tex]\overrightarrow{OC}[/tex] sur ton dessin, tu l'aurais vu tout de suite...

Je n'ai peut-être pas été assez clair, alors j'explicite ma pensée :
En traçant [tex]\overrightarrow{OC}(0\,;\,4)[/tex] tu te serais aperçue que :
1. Avec ces coordonnées le vecteur était "vertical",
2. Et donc que C était placé sur l'axes des ordonnées,
3. Sur le dessin fourni, le point C figurait, mais pas là sur l'axe des ordonnées,
4. Qu'il était impossible avec ton placement de construire un carré ABCD.

Ainsi tu aurais été alertée plus tôt et découvert ton étourderie...

@+

Dernière modification par yoshi (29-01-2019 09:24:32)

Schéhérazade · 29-01-2019 12:12:50

Bonjour

je reprends mon raisonnement:

on a xB=2 et xA=-2 donc AB=4. ABCD est donc un carré de coté 4;donc BC=4.
OB=2 donc xB=xC=2.
On a donc C(2;4).

vectOC'((2racine carré 5)/5 ; (4 racinecarré 5)/5) et vectOC (2;4)
donc: (2racine carré 5)/5*4= (8racine5)/5
et: (4racine5)/5*2=(8racine5)/5
donc (2racine carré 5)/5*4=(4racine5)/5*2 donc vecOC' et vecOC sont colinéaires; O,C', et C sont alignés: C' appartient à (OC).

Est ce correct?

Merci beaucoup

yoshi · 29-01-2019 12:25:42

Re,

Oui... bien sûr !

Si je "chipote", ici :

OB=2 donc xB=xC=2.

Le donc me dérange un peu...
OB=2 ne prouve pas que [tex]x_B=2[/tex] : avec OB=2 on pourrait avoir aussi $x_B=-2$
Mais c'est l'énoncé qui donne [tex]x_B=2[/tex]
Puisque ABCD est un carré, alors [tex](BC)\perp(AB)[/tex].
Or, $y_A=y_B=0$ d'où [tex]x_C=x_B=2[/tex]

@+

Schéhérazade · 29-01-2019 12:50:22

re

j'ai enlevé le ''donc'' dans ma démonstration XD

j'ai un autre problème: je ne comprends pas la question 2a)''Quel est le rapport de l'homothétie h?''
comment on calcule le rapport d une homothétie? Je me souviens l avoir déjà appris mais là je bloque

Merci

yoshi · 29-01-2019 13:20:02

Re,

C' étant l'image de C dans l'homothétie h de centre O et de rapport k ($ \neq 0$) tu peux écrire : [tex]\overrightarrow{OC'}=k.\overrightarrow{OC}[/tex]
Mais, en 3e, si tu as bien vu l'homothétie, tu as - au mieux - à peine effleuré les vecteurs...
En 3e, si C et C' sont sur la même demi-droite d'origine O, alors on dit que le rapport est positif (et négatif dans le cas contraire)...
Le risque dans le dernier cas, c'est que quelqu'un écrive, si M--> M' et $O \in [MM']$, que OM'=k.OM avec un rapport négatif, ce qui n'a pas de sens...
Donc en 3e, si, par ex, le rapport est -2, on se contente de dire que M' et M ne sont pas sur la même demi-droite d'origine O et d'écrire que OM'=2OM.

Ici la question ne se pose pas. Tu signales quand même que le rapport est positif et tu travailles avec des longueurs : OC'= k.OC.

(Evidemment si tu as vu le travail vectoriel en classe, tu peux utiliser les vecteurs, mais j'ai l'impression que vous n'avez pas encore revu les homothéties, cette année ?)

@+

Schéhérazade · 30-01-2019 12:22:50

re

donc la réponse est ''le rapport de l'homothétie h est positif'' et il n y a pas de calcul à faire?
ou bien j ai mal compris?

Merci

Schéhérazade · 30-01-2019 12:49:58

re
est ce que le rapport de l homothetie est : h= OC'/OC
OC'=2
et OC= racine carré 20
donc h= 2/racine20
=(racine5)/5
env=0,45

est ce correct?

Merci

yoshi · 30-01-2019 13:07:45

Salut,

Attention ici, h est le nom que ton prof a donné à l'homothétie de centre O qui transforme C en C' : [tex]C'=h(C)[/tex].
Ton rapport k est effectivement [tex]\dfrac{OC}{OC'}=\dfrac{2}{2\sqrt 5}=\dfrac{\sqrt 5}{5}[/tex]

env=0,45
est ce correct?

Ça, par contre, c'est une mauvaise habitude à proscrire...
Que [tex]k \approx 0,45[/tex], on s'en fiche éperdument, sauf si l'énoncé te le demande explicitement et ici ce n'est pas le cas.
Les calculs se feront en utilisant la valeur exacte : [tex]k= \dfrac{\sqrt 5}{5}[/tex]...

@+

Schéhérazade · 30-01-2019 16:03:20

Re

j'ai terminé la partie 1.
Pouvez vous m aider pour la partie 2:

Partie B
3.Un triangle équilatéral IJK étant donné et en s'inspirant éventuellement des questions précédentes, construire un carré ABCD inscrit dans le triangle , c est à dire tel que: A,B appartiennent à [IJ], C appartienne à [JK] et D appartient à [IK].

On donnera les différentes étapes de la construction et on démontrera que le quadrilatère ainsi construit répond bien au problème posé.

je ne sais pas comment commencer

Merci bcp

yoshi · 30-01-2019 22:20:16

Bonsoir,

je ne sais pas comment commencer

Et bien, ça ne me surprend pas: je trouve ça particulièrement difficile pour un élève de 2nde...
A partir du carré, construire un triangle équilatéral autour aurait été bien plus simple...

J'ai galéré un moment avant d'obtenir une solution que je trouve bien trop compliquée (pas loin de 2 pages avec les justifications) , surtout si par hasard tu devais expliquer le tout à ton prof sans ta copie sous les yeux...

Je te livre le résultat seul : tu traces un triangle équilatéral IJK de côté 10.
Tu places O le milieu de [IJ], tu appliques une homothétie de centre O et de rapport $k= 2(2-\sqrt 3)$ qui transforme K en M.
M sera le milieu de [CD], $OM =10(2\sqrt 3-3)$
A partir de C et D sur [JK] et [IK], tu déduis B et A sur [IJ].
Si tu connais Geogebra, place I(-5, ; 0), J(5 ; 0), $K(0\,;\, 5\sqrt 3)$ et O(0 ; 0).

Je réfléchirai à nouveau demain pour voir si je trouve qq ch de plus simple ; peut-être quelqu'un passera-t-il avec une autre idée...

@+

Schéhérazade · 31-01-2019 10:55:42

Re

vous dites:

yoshi a écrit :

tu traces un triangle équilatéral IJK de côté 10.

Moi j avais compris qu il fallait utiliser la figure donnée dans la partie 1, ou on a déjà les points I et J du triangle IJK.

Peut etre que je me trompe ?

Merci

yoshi · 31-01-2019 12:27:57

Salut,

J'ai trouvé une méthode simplissime...
Mais d'abord je réponds à ta question...

3.Un triangle équilatéral IJK étant donné et en s'inspirant éventuellement des questions précédentes, construire un carré ABCD inscrit dans le triangle , c est à dire tel que: A,B appartiennent à [IJ], C appartienne à [JK] et D appartient à [IK].

Un triangle équilatéral IJK étant donné
Tu pars d'un triangle équilatéral donné...
Dans ton énoncé, partie 1, j'ai beau le relire je ne trouve pas où on a déjà les points I et J du triangle IJK.
Certes les repères orthonormés sont souvent appelés (O,I,J) avec I(1 ; 0) et J(0 ; 1)...
D'ac, je vois, ils sont sur le dessin mais les points ABCD aussi et avec d'autres coordonnées..
Mais le point K, ne figure pas...
En plus il n'est pas écrit le triagle, mais : étant donné un triangle équilatéral
Donc moi je pars de quelque chose de neuf... question à poser à ton prof.
De toute façon, la méthode que je vais te proposer est adaptable.

Voià.
Je pars d'un triangle équilatéral IJK. J'appelle M le milieu de [IJ]
Sur [MI] je place A', et [MJ], je place B' tels que M soit le milieu de [A'B']
Tu construis, soit en le faisant rester à l'intérieur du triangle équilatéral (s'il est assez grand), soit qui déborde (si tu prends les I et J de ta figure), un carré A'B'C'D'.
Les demi-droites [MC') et [MD') coupent respectivement [JK] et [IK] en C et D.
Depuis C et D tu abaisses les perpendiculaires sur [IJ] : tu obtiens respectivement les points B et A cherchés...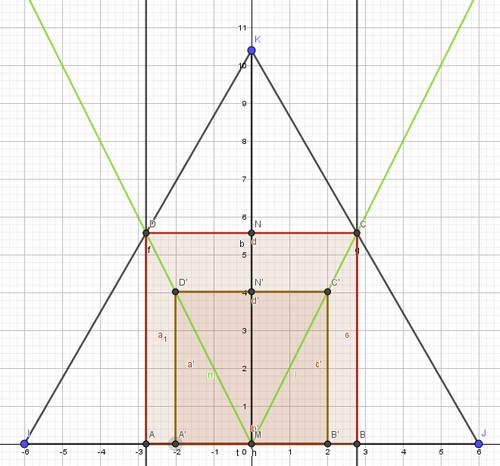

Justifications.
Es-tu capable de justifier si j'appelle h l'homothétie de centre M et de rapport OC/OC' dans laquelle h(C')=C, on a H(D')=D, h(A')=A et H(B')=B ? Et que ABCD est la figure homothétique du carré A'B'C'D' et par conséquent un carré aussi ?
Coup de pouce : Thalès.

Après, je te dirai comment l'idée m'est venue...

@+

Schéhérazade · 02-02-2019 13:01:57

Re

J ai bien cherché j ai lu et relu pourtant je n arrive pas du tout a prouver que ABCD est la figure homothétique de A'B'C'D' .

Pouvez vous m aider svp je bloque vraiment et je dois rendre le dev lundi..

Merci encore pour votre aide

Schéhérazade · 02-02-2019 15:33:26

Re

J ai revu votre raisonnement et il y a qqchose que je n ai pas compris.

Pourquoi est ce que on a besoin de prouver que ABCD est la figure homothétique de A'B'C'D' pour pouvoir dire que c est un carré?
Pourquoi on ne peut pas dire directement " une fois qu on a les points C et D ,on construit les points A et B sur (IJ) tel que ABCD soit un carré" ?

Merci encore

Schéhérazade · 02-02-2019 15:53:37

J ai quand mm fait la démonstration avec Thalès:

Dans le triangle DMC, on a:
•D,D' et M sont alignés puisque (MD') coupe (IK) en D,
•M,C' et C sont alignés puisque (MC') coupe (IJ) en C.

On peut donc utiliser le théorème de Thalès, on a donc:

(MC/MC')=(MD/MD')=(DC/DC')

A partir de ça comment prouver que ABCD est la figure homothétique de A'B'C'D' ?

Merci

yoshi · 02-02-2019 16:23:15

Re,

Pourquoi on ne peut pas dire directement "une fois qu on a les points C et D , on construit les points A et B sur (IJ) tel que ABCD soit un carré" ?

C'est tentant, bien sûr...
En réponse, je te pose la simple question : qu'est-ce qui prouve que (CD) est parallèle à (IJ) ?
A partir de [CD] tu construis un carré dis-tu... Mais si (CD) n'est pas parallèle à (IJ), (AB) ne pourra pas être un segment de [IJ]...
En admettant que tu saches que (CD) //(IJ), tout ce que tu peux construire sans démonstration est un rectangle, et il restera à prouver, par ex, que CD = CB, alors tu pourras dire : c'est un carré...
Le plus difficile est de prouver que (CD)//(C'D') //(IJ).
Vois-tu, je travaille depuis ce matin à prouver ça de la façon la plus simple possible pour toi, pour que tu sois capable de la refaire seule.
Je t'avais dit : ce n'est pas facile pour une élève de 2nde.

--------------------------------------------------------

Tu ajoutes que tu appelles N et N' les intersections respectives de [CD] et et [C'D'] avec [MK].

Je te propose deux solutions. Tu choisis la 1 ou la 2.
La méthode 2 est la plus rigoureuse, elle utilise une homothétie. La méthode 1, est moins rigoureuse, mais plus facile, moins technique, des détails sont passés sous silence volontairement et ton prof risque moins de te dire que tu n'as pas trouvé ça toute seule...
Tu fais comme tu préfères.

Méthode 1.
Il faut remarquer faire remarquer qu'il a été construit un carré A'B'C'D', M et N' les milieux de [A'B'] et [D'C'].
Quelle que soit la valeur du côté de ce carré, dans le triangle MC'B' rectangle en N', la tangente de l'angle [tex]\widehat{C'MB'}[/tex] est toujours égale à 2 (MB' = MN'/2 = C'B'/2).
Donc que quelle que soit la longueur du côté A'B'C'D', l'angle que fait (MC) avec (MB), donc avec [MJ), ne change pas.

Donc, on prend un point C n'importe où sur [MC'), on trace la parallèle à (IJ) passant par C elle coupe (MN') en N ; on trace la perpendiculaire à (MJ) passant par C : elle coupe [MJ] en B.
Le quadrilatère ainsi construit est un rectangle et CB = MN'= 2 MB. C'est la moitié d'un carré.
Ce qui est vrai avec le triangle C'MB' est vrai aussi pour le triangle MA'D' : (MN) est un axe de symétrie...
Donc si je prolonge [CN] elle va couper la demi-droite [MD') en un point que j'appelle D : cela revient à construire le symétrique du triangle MKJ (et de tout ce que contient le demi-plan de frontière (MK) et contenant J) par rapport à (MK) : le point C donne le point D, le rectangle MNCB, donne un rectangle MNDA.
Ce rectangle MNDA est aussi la moitié d'un carré.
Les rectangles MNDA et MNCB ont le côté [MN] en commun, donc ABCD est un carré.
Donc (CD)//(AB) donc (C'D')//(A'B').
Puisqu'on peut prendre C n'importe où sur [MC'), on le prend à l'intersection de [MC') avec [KJ] et D à l'intersection de [MD') avec [KI]

Méthode 2
Pour appliquer Thalès, je suis obligé de montrer aue (CD) // (C'D')//(IJ)
IJK est un triangle équilatéral donc en particulier KI =KJ.
Le point K, équidistant de des extrémités de [IJ], est donc sur la médiatrice de [IJ]
Cette médiatrice passe par le milieu de [IJ] qui est M, donc (KM) est la médiatrice de [IJ] et un axe de symétrie du triangle.
N' est le milieu de [C'D'] puisque M est celui de [AB].

Tu considères maintenant la symétrie axiale d'axe (KM).
Dans cette symétrie :
[KJ] est le symétrique du côté [KI]
M est son propre symétrique.

AB'C'D' est un carré, [A'B'] //'(D'C') et M milieu de [A'B'] par construction.
C' donc est le symétrique de D'

Quel est alors le symétrique de D ?
D est sur [KI], donc son symétrique appartient au segment symétrique de [KI], c'est à dire [KJ]
D est sur (MD'), donc son symétrique est sur la droite symétrique de (MD'), c'est à dire (MC').
Le symétrique de D est sur [KJ] et (MD') : ce symétrique est donc à l'intersection de [KJ] et (MC'), c'est donc C.

Donc (DC)⊥(MK)
et donc (DC)//(D'C')//(A'B')

Maintenant, on peut utiliser le th de Thalès
(Mon commentaire à ne pas écrire sur la copie : ça va tout seul... On utilise les triangles MCN, MDN, MCA, MDB : il y a a chaque fois un côté commun et donc un rapport commun)
Je note k le rapport [tex]\dfrac{MC}{MC'}[/tex]

Dans le triangle MNC,
N' est sur [MN], C' est sur [MC] et (N'C')// (NC)
Maintenant on peut appliquer le théorème de Thalès :
[tex]\dfrac{MN}{MN'}=\dfrac{MC}{MC'}[/tex]
J'ai donc
[tex]\dfrac{MN}{MN'}=\dfrac{MC}{MC'}=k[/tex]

Je recommence dans le triangle MND
Et j'arrive à :
[tex]\dfrac{MD}{MD'}=\dfrac{MN}{MN'}[/tex]
et donc à
[tex]\dfrac{MD}{MD'}=k[/tex]

Je recommence dans le triangle MCB :
ici, on a (C'B')//(CB).
D'où
[tex]\dfrac{MB}{MB'}=\dfrac{MC}{MC'}=k[/tex]

Puis dans le triangle MDA :
Ici on a (D'A')//(C'B')
[tex]\dfrac{MA}{MA'}=\dfrac{MD}{MD'}=k[/tex]

Tu choisis l'homothétie de rapport k et de centre M telle que h(C')=C (donc de rapport k) et dans cette homothétie h(D')=D, h(A')=A, h(B')=B puisque [tex]\dfrac{MA}{MA'}=\dfrac{MC}{MC'}=\dfrac{MD}{MD'}=\dfrac{MB}{MB'}=k[/tex]

@+

[EDIT]Difficile d'expliquer correctement quoi que ce soit : manque de réactivité...

Dernière modification par yoshi (03-02-2019 12:22:03)

Schéhérazade · 03-02-2019 15:49:53

Re
Je suis désolée de pas avoir répondu plus tôt mais j ai pas mal de travail..

J ai choisi la méthode 1 et il y a plusieurs points que je n ai pas compris:

•premierement, vous dites ''la tangente de l angle C'MB' est toujours égale a 2 ( C'MB'= MN'/2=C'B'/2)" . Je ne comprends pas en quoi l égalité que vous avez mis entre parenthèse prouve que la tangente a l angle C'MB' ( qui est donc MB' ) est tjrs égale a 2.

•Ensuite : vous dites '' CB= MN'=2MB'".Je ne comprends pas d ou vient cette égalité?comment on prouve que MN'=2MB?

• Autre chose: vous dites "(MN') est un axe de symétrie''.Comment le prouver?Ou bien ce n est pas important de le prouver?

•Dernier point: a la fin du raisonnement, vous dites " Puisqu'on peut prendre C n'importe où sur [MC'), on le prend à l'intersection de [MC') avec [KJ] et D à l'intersection de [MD') avec [KI]
Je ne comprends pas a quoi sert de dire ou on place D alors que vous avez déjà doné la position de D au cours du raisonnement :" Donc si je prolonge [CN] elle va couper la demi-droite [MD') en un point que j'appelle D ''.

Merci bcp pour votre aide

yoshi · 03-02-2019 16:16:19

Re,

Si tu prends le carré A'B'C'D', que tu prends M milieu de [A'B'] et N' milieu de [C'D'] ton carré est coupé en 2 rectangles : MN'B'C' et MND'A' qui sont la moitié du carré
.
En effet tu as C'D' = A'B' = B'C' = D'A'
M milieu de [A'B'] donc MA'=MB' = A'B'/2 = B'C'/2
Maintenant, prends le triangle rectangle MC'B', on a
[tex]\tan \widehat{C'MB'}= \dfrac{C'B'}{MB'}=2[/tex] et ça c'est toujours vrai. Et l'angle toujours le même...
Donc à partir de M et en restant sur (IJ), si tu places un point B n'importe où sur [MJ) et que tu construis un rectangle tel que MBCN, avec N sur [MN') et tel que MN' = BC = 2MB Où va être le point C ?
Et bien avec ce que je viens de dire : sur [MC')

Et puisque dans le triangle équilatéral, les 3 médiatrices, les 3 médianes, les 3 hauteurs et les 3 bissectrices sont confondues, que ce triangle a 3 axes de symétrie, la médiane [MK] qui est aussi médiatrice est l'un des axes de symétrie.
Et puisqu'on peut placer C n'importe où sur [MC'), il y a un endroit qui va bien : à l'intersection avec [KJ].
Et dans la symétrie d'axe (MK), le symétriique MNDA du rectangle MNCB est un rectangle égal qui est aussi une moitié de carré.
Et ABCD contient les deux rectangles moitiés de carré est donc un carré...

La suite d'ici 2 bonnes heures : je suis en retard. J'ai à faire...

@+

yoshi · 03-02-2019 19:48:46

RE,

Oublie ce que j'ai pu dire avant le post #19.
Je reprends.
Je ne construis au départ que le rectangle MN'C'B' qui est la moitié du carré A'B'C'D' : $MN'=2MB'$, puis j'ai placé B1 et B2 n'importe où sur [MJ) et je construis 2 autres rectangles en partant de B1 et B2 avec [tex]B_1C_1 = 2MB_1[/tex] et [tex]B_2C_2 = 2MB_2[/tex]
Dans le triangle C'MB' rectangle en B'
[tex]\tan(\widehat{C'MB'})=\dfrac{C'B'}{MB'}=\dfrac{2M'B'}{MB'}=2[/tex]

Voici le demi-triangle équilatéral MKJ et les 3 rectangles ayant un sommet en M et tels que leur longueur est le double de leur largeur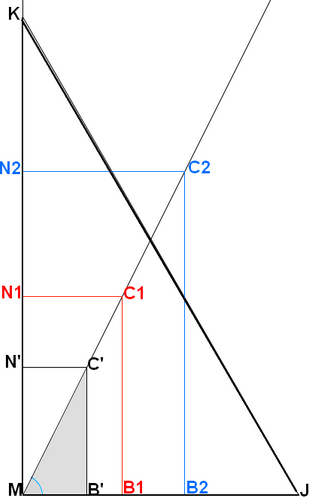

$MN_1=2MB_1$
$MN_2=2MB_2$
Tu peux constater que les points $C_1$ et $C_2$ sont placés sur [MC')
Ce sont chacun la moitié d'un carré : il suffit de construire les rectangles demi-carrés symétriques par rapport à (MK) de ceux existant pour obtenir autant de carrés.
Peu importe où est placé un point B sur la demi-droite [MJ), on trace la perpendiculaire à (MJ) passant par B, : elle coupe [MC') en un point que j'appelle C.
De C je trace la perpendiculaire à [MN') qui coupe [MN') en un point que j'appelle N.
Le quadrilatère MNCB a trois angles (droits (donc le 4e l'est aussi), c'est un rectangle.
Suis-je sûr que c'est un demi-carré ?
Oui, parce que dans le triangle MCB rectangle en B
[tex]\tan(\widehat{CMB})=\dfrac{CB}{MB}[/tex]
L'angle $\widehat{CMB}$ est un autre nom de l'angle $\widehat{C'MB'}$ dont la tangente est 2.
Donc $\dfrac{CB}{MB}=2$ et [tex]CB=2MB[/tex]
Donc CB = MN= 2MB = 2 NC...

Si je construis le rectangle MNDA symétrique par rapport à (MK) du rectangle MNCB il sera aussi tel que AD = MN = 2 MA = 2ND.
Car, propriétés de la symétrie : elle conserve les longueurs, les angles...

M et N sont sur l'axe de symétrie donc le symétrique de M est M, le symétrique de N est N.
Le symétrique de C s'appelle D, le symétrique de B s'appelle A.
Donc
* le symétrique de [MB] et [MA] et MA = MB donc AB= 2 MB
* le symétrique de [BC] est [AD] et BC = AD et AD = MN = BC
Or on a montré plus haut que BC = 2MB donc, AB = Bc et enfin AB = BC = CD= DA, j'ai bien un carré.

Mais au lieu de placer B (n'importe où sur [MJ)) pour trouver C sur [MC'), je peux placer C n'importe où [MC'), puis tracer la perpendiculaire passant par C à [MJ) qui me donne B et la perpendiculaire à [MN') passant C qui me donne N...
Et par symétrie par rapport à (MK), j'obtiens l'autre rectangle demi-carré MNDA : ABCD est alors un carré...
Puisque je peux prendre C n'importe où sur [MC') alors je vais le prendre à l'intersection de [MC') et de [KJ) et au lieu de construire un rectangle puis l'autre je construis B et puis D intersection de la perpendiculaire à (MN) passant par C et de [MI] puis A pied de la perpendiculaire abaissée de D sur [MI).

La seule question est maintenant : (MK) est-il un axe de symétrie pour le triangle équilatéral IJK ?
Oui.
Les axes de symétrie sont les médiatrices des côtés et ils passent par les sommets opposés.
(MK) est bien la médiatrice de [IJ]
KI = KJ, donc le point K, équidistant des extrémités de [IJ], est donc sur la médiatrice de [IJ]
Cette médiatrice passe par le milieu de [IJ] qui est M, donc (KM) est la médiatrice de [IJ] et un axe de symétrie du triangle.

Ça te va ?

@+

Schéhérazade · 04-02-2019 14:23:30

oui j ai bien compris le raisonnement merci beaucoup pour votre aide!

Forum de mathématiques - Bibm@th.net

#1 28-01-2019 15:42:32

Devoir seconde vecteur

#2 28-01-2019 16:20:10

Re : Devoir seconde vecteur

#3 28-01-2019 20:14:38

Re : Devoir seconde vecteur

#4 29-01-2019 09:23:47

Re : Devoir seconde vecteur

#5 29-01-2019 12:12:50

Re : Devoir seconde vecteur

#6 29-01-2019 12:25:42

Re : Devoir seconde vecteur

#7 29-01-2019 12:50:22

Re : Devoir seconde vecteur

#8 29-01-2019 13:20:02

Re : Devoir seconde vecteur

#9 30-01-2019 12:22:50

Re : Devoir seconde vecteur

#10 30-01-2019 12:49:58

Re : Devoir seconde vecteur

#11 30-01-2019 13:07:45

Re : Devoir seconde vecteur

#12 30-01-2019 16:03:20

Re : Devoir seconde vecteur

#13 30-01-2019 22:20:16

Re : Devoir seconde vecteur

#14 31-01-2019 10:55:42

Re : Devoir seconde vecteur

#15 31-01-2019 12:27:57

Re : Devoir seconde vecteur

#16 02-02-2019 13:01:57

Re : Devoir seconde vecteur

#17 02-02-2019 15:33:26

Re : Devoir seconde vecteur

#18 02-02-2019 15:53:37

Re : Devoir seconde vecteur

#19 02-02-2019 16:23:15

Re : Devoir seconde vecteur

#20 03-02-2019 15:49:53

Re : Devoir seconde vecteur

#21 03-02-2019 16:16:19

Re : Devoir seconde vecteur

#22 03-02-2019 19:48:46

Re : Devoir seconde vecteur

#23 04-02-2019 14:23:30

Re : Devoir seconde vecteur

Pied de page des forums