Forum de mathématiques - Bibm@th.net

ccapucine

Membre

Inscription : 19-05-2018

Messages : 180

choix de y_0 pour edo

Bonjour
j'ai du mal avec la question suivante: calculer la valeur de $y_0$ pour laquelle la solution du problème qui suit touche l'axe des x mais ne le coupe pas
$$
y'+(2/3)y=1-1/x,\; y(0)=y_0.
$$
Merci par avance pour toute indication

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 047

Re : choix de y_0 pour edo

Bonsoir,

  Je ne sais pas si c'est la méthode la plus directe, mais as-tu chercher la solution générale de cette équation?

F.

Black Jack

Membre

Inscription : 15-12-2017

Messages : 470

Re : choix de y_0 pour edo

Bonjour,

L'équation n'est pas définie en x = 0, et donc y(0) n'a pas de sens, me semble-t-il.

A partir des données, il me semble qu'on peut dire que pour une certaine valeur a de x on, a : y(a) = 0 et y'(a) = 0 (touche l'axe des x sans le couper --> extremum local)

On a alors a = 1

Donc la fonction f solution est telle que f(1) = 0

Si on utilise cette condition et qu'on calcule par une méthode numérique, il semble bien  que lim(x-->0+) f(x) = +oo et que lim(x-->0+) f'(x) = -oo

Mais peut-être me trompe-je.

Matou

Invité

Re : choix de y_0 pour edo

Bonjour,

Je pense que Black Jack a raison jusqu'à "la fonction f solution est telle que f(1) = 0".

Ensuite, je pense qu'il faut regarder du côté de la formule de Duhamel. Attention, les calculs font intervenir des fonctions assez peu sympathiques

Matou

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 047

Re : choix de y_0 pour edo

Hello

  Pourquoi est ce qu'alors on ne peut pas dire en dérivant encore une fois que  $ f''(1)=1 $ et donc que f admet effectivement un minimum en 1.

F

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 047

Re : choix de y_0 pour edo

Je m'auto réponds. Ca ne prouve pas que la courbe ne coupe pas l'axe ailleurs...

Black Jack

Membre

Inscription : 15-12-2017

Messages : 470

Re : choix de y_0 pour edo

Bonjour,

"la solution du problème qui suit touche l'axe des x mais ne le coupe pas"

On peut penser qu'au point correspondant, f a un extremum ou un point anguleux ou un point de rebroussement ... mais dans ces 2 derniers cas, f ne serait pas dérivable au point considéré et donc l'équation différentielle n'aurait pas de sens.

Il me semble donc que la seule possibilité envisageable est un extremum local (y'(a) = 0 et y(a) = 0) ... qui conduit à a = 1

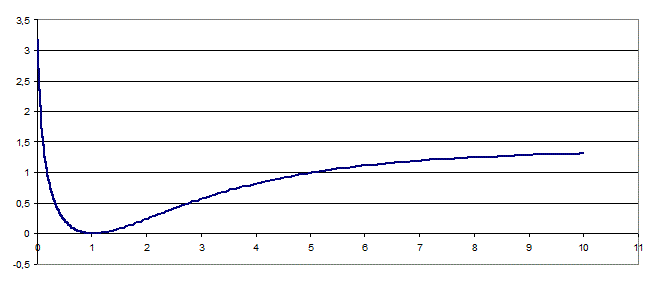
On a donc une équation différentielle d'ordre 1 avec un condition (y(1) = 0) ... et si on résout numériquement à partir de là (par petits incréments ou décréments), on trouve bien une courbe à un seul extremum (qui est un minimum en x = 1 et y = 0).
On voit aussi sur la courbe ainsi tracée que f(x) "grandit" très fort pour x --> 0+

Ce n'est pas une solution de matheux (que je ne suis pas), mais une approche à la "ingénieur" qui permet de voir où on met les pieds.

Je pense qu'on peut montrer que pour x proche de 0+, f(x) [tex]\simeq[/tex] -ln(x) convient comme solution.

Probablement sans assez de rigueur, ainsi :

pour x proche de 0+, on a :

y' + (2/3)y = -1/x (car |1/x| > > > 1)

Si y = -ln(x)
y' = -1/x

y'/y = x.ln(x) = ln(x)/(1/x)

lim(x--> 0+) y'/y = (par Lhospital) lim(x--> 0+) (1/x)/(-1/x²) = lim(x--> 0) [-x] = 0

et donc près de 0+, |y'| < < |y| , l'équation différentielle est vérifiée.

Près de 0+, une solution de l'équation différentielle est f(x) [tex]\simeq[/tex] -ln(x)

Et donc, comme pressenti, y(0+) = lim(x-->0+) -ln(x) = +oo

De toutes manières, la question posée (trouver la valeur de y(0)) n'a pas de sens.

Il serait intéressant d'avoir un énoncé complet et non interprété (je suppose qu'il l'est) pour pouvoir avancer avec visibilité.

Matou

Invité

Re : choix de y_0 pour edo

Bonsoir,

j'ai a moitié dit une bêtise tout à l'heure. La réponse de Black Jack est complètement juste.

La fonction n'est effectivement pas définie en 0.

En fait, j'ai considéré que la valeur de y0 c'est le terme qui multiplie la solution générale sans second membre ainsi que l'on fait usuellement avec la formule de Duhamel. Il reste que les calculs sont assez fastidieux

Matou

ccapucine

Membre

Inscription : 19-05-2018

Messages : 180

Re : choix de y_0 pour edo

Je n'avais pas de connexion et je viens à l'instant d'y avoir accès. Merci pour toutes ces réponses, je vais répondre demain je l'espère.

ccapucine

Membre

Inscription : 19-05-2018

Messages : 180

Re : choix de y_0 pour edo

Je ne suis pas très d'accord. En effet il est peut être possible de la prolonger en $x_0=0$. Non?
Alors comme l'équation n'est pas définie en $x=0$, je cherche une solution au voisinage d'un point $x_0 \neq 0$ puis je regarde si on peut la prolonger en $0$.
On résout le problème $y'+2/3 y =1 - 1/x, y(x_0)=y_0$ telle que $x_0 \neq 0$.
La solution général de l'edo homogène associée est:
$ y_h(x)= C e^{-2/3 x}$ où $C$ est une constante réelle quelconque. On cherche une solution particulière de la forme $y_p(x)= C(x) e^{-2/3 x}$. En l'injectant dans l'équation on obtient $C'(x)= e^{2/3 x}- 1/x e^{-2/3 x}$ qui implique que $C(x)= \displaystyle\int_{x_0}^x e^{2/3 s} ds - \displaystyle\int_{x_0}^x 1/s e^{-2/3} s ds$. Puis je bloque car l'ipp ne donne rien.

Dernière modification par ccapucine (24-11-2018 00:37:56)

Michel Coste

Membre

Inscription : 05-10-2018

Messages : 1 114

Re : choix de y_0 pour edo

Aucune solution dérivable ne peut être définie sur un intervalle contenant $0$.

Black Jack

Membre

Inscription : 15-12-2017

Messages : 470

Re : choix de y_0 pour edo

Bonjour :

Image de la solution avec les conditions de l'énoncé :

x en abscisses, f(x) en ordonnées

Si x --> +oo, f(x) --> 3/2
Si x --> 0+, f(x) --> +oo