Second degré

Lauryne972 · 17-02-2018 21:00:41

Bonjour,j'ai un exercice de maths que je n'arrive pas à comprendre. Pourriez vous m'aider s'il vous plaît.
Voici l'énoncé:
Une entreprise produit et vend un certain produit au prix de 8,50€.On note x le nombre de milliers d'articles fabriqués chaque mois avec 0<=x<=14.Le coût de production,en milliers d'euros,de x milliers d'articles est donné par C(x)=0,5x^2+x+10,72.
1)Quels sont les coûts fixes?
2)L'entreprise a produit et vend 14000 produits.A-t-elle réalisé un bénéfice ?
3)Montrer que le bénéfice,exprimé en milliers d'euros,réalise pour la vente de x milliers d'articles est B(x)= -0,4x^2+6x-8,1.

Merci d'avance pour votre aide .

yoshi · 17-02-2018 22:39:12

Bonsoir,

Alors avant toute chose, une précision de taille : je n'ai jamais fait d'économie !
Pourtant, je vais te répondre : j'ai cherché un cours sur Internet et y ai trouvé confirmation de ce que je pensais : les coûts fixes sont indépendants des quantités produites...
Alors, dis-moi, cela ne figure pas dans ton cours ???
En conséquence : Coûts fixes = C(0) !

2. Le bénéfice, c'est la différence qui reste en caisse avec l'argent des ventes et les coûts de production.
[tex]B(x)=8,5x-C(x)[/tex]. 8,5x c'est 8,5 * 14000 ce qui va bien te donner (8,5 * 14) milliers d'euros
Ici [tex]B(14000)= 8,5\times 14000 -C(14000)[/tex]
Si le résultat est positif, il y a bénéfice, dans le cas contraire, il y a perte...

3. Mais là, je suis face à un problème. J'aurais dit :
[tex]B(x)=8,5x-C(x)=8,5x-(0,5x^2+x+10,72)[/tex]
Mais ça ne colle pas avec la formule donnée. Et ce soir, je ne suis pas en situation de réfléchir...
Pour arriver à [tex]B(x)=-0,4x^2+6x-8,1[/tex], il faudrait faire [tex]0,1x^2+7x+2,1 - (0,5x^2+x+10,72)[/tex]
Pourquoi le prix de vente de x milliers d'articles à 8,5 € s'exprimerait-il par [tex]0,1x^2+7x+2,62[/tex] ???
Quelque chose cloche vraiment !
Et pourtant, cet exercice me donne raison : http://www.bibmath.net/forums/viewtopic.php?id=8733
Ou encore cet autre http://www.bibmath.net/forums/viewtopic.php?id=7 Partie II question 3a)
Alors que faut-il conclure ?
Ton énoncé est-il exact ? Rien ne manque ?

@+

@+

Lauryne972 · 17-02-2018 23:34:40

Bonsoir,
Pour vous répondre clairement,non cela ne figure pas dans mon cours et quand je cherche sur internet,je suis dans le floue totale ,c'est pour cela que je suis venue demander de l'aide.
Cependant pour la question 2 et 3 ,j'avais fait comme vous,mais pour la question 3,Je ne trouvais pas la formule exacte ,donc je pensais que c'était moi qui m'étais trompée,mais je vois que je ne suis pas la seule !Je pense donc qu'il ya un sans doute un problème dans l'énoncé.
Je vous remercie pour votre aide.
Bonne soirée.

yoshi · 18-02-2018 11:07:58

Bonjour,

Cependant pour la question 2 et 3 ,j'avais fait comme vous,mais pour la question 3, je ne trouvais pas la formule exacte ,

Donc, cette affirmation :

j'ai un exercice de maths que je n'arrive pas à comprendre.

est inexacte : seule la question 3. posait problème.
Le dire comme ça, aurait été mieux pour moi.

Ce matin, avec les idées plus claires, je me suis dit que la formule exprimant le bénéfice [tex]B(x)=-0,4x^2+6x-8,1[/tex] était très "louche"...
Alors j'ai cherché pour voir si on pouvait trouver cet énoncé quelque part : et j'en ai trouvé un très très voisin (mêmes données) mais bien plus complet.
Le voici :

Une entreprise fabrique et commercialise un certain produit. Sa capacité de production mensuelle est inférieure à 14 milliers d’articles.
On note x le nombre de milliers d’articles fabriqués chaque mois.
Le coût de production, exprimé en milliers d’euros, est alors modélisé par la fonction C définie, pour tout [tex]x \in [0\,;\, 14][/tex], par : [tex]C(x) = 0,5x^2 + x + 10,72[/tex]
On admet que chaque article fabriqué est vendu au prix unitaire de 8,50 €.
1. Est-il plus avantageux pour l’entreprise de fabriquer et vendre 7 000 articles ou de fabriquer et vendre 9 000 articles?
2. À l’aide de la calculatrice, faire un tableau de valeurs de la fonction C sur l’intervalle [tex][0\,;\, 14][/tex] avec un pas de 1 (arrondir à l’unité) puis tracer dans un repère sa représentation graphique c .
Unités : 1cm pour 1 unité sur l’axe des abscisses; 1cm pour 10 unités sur l’axe des ordonnées La courbe sera obligatoirement tracée avec soin sur une feuille à petits carreaux ou sur du papier millimétré.
3. On désigne par R(x) le montant, en milliers d’euros, de la recette mensuelle obtenue pour la vente de x milliers d’articles.
a) Donner l’expression R(x) en fonction de x puis tracer, sur le même graphique, la droite représentative de la fonction R.
b) Par lecture graphique déterminer l’intervalle dans lequel doit se situer la production x pour que l’entreprise réalise un bénéfice positif.
4. Le bénéfice mensuel, exprimé en milliers d’euros, réalisé lorsque l’entreprise produit et vend $x$ milliers d’articles est modélisé par la fonction B définie sur l’intervalle [tex][0\,;\, 14][/tex].
a) Montrer que pour tout réel x de l’intervalle [tex][0\,;\, 14][/tex] on a : [tex]B(x) = – 0,5x^2 +7,5x – 10,72[/tex]
b) Étudier le signe de B(x). En déduire la plage de production qui permet de réaliser un bénéfice (positif).
c) Déterminer, en justifiant, le tableau de variations de la fonction B sur [0; 14].
d) En déduire le nombre d’articles qu’il faut fabriquer et vendre chaque mois pour obtenir un bénéfice maximal. Quel est le montant, en euros, de ce bénéfice maximal ?

Et qu'est-ce que j'ai bien pu y voir qui me pousse à reposter ?
Mais la formule du bénéfice :
[tex]B(x) = – 0,5x^2 +7,5x – 10,72[/tex]
Qui correspond à
[tex]B(x)=8,5x -(0,5x^2+x+10,72)=8,5x -0,5x^2-x-10,72 = -0,5x^2+7,5x-10,72[/tex]
Soit exactement ce que je te proposais...

Et j'en reviens à l'énoncé qu'on t'a donné...

Au passage, l'énoncé ci-dessus est rangé en rubrique économie, mais avec 10% de bon sens, il ne manque plus que 90% de techniques mathématiques communes aux 1eres S et ES : vraiment pas très difficile...

@+

Lauryne972 · 18-02-2018 12:12:42

Bonjour,je vois ce que vous voulez me dire.
Merci pour votre aide .

yoshi · 19-02-2018 19:35:30

Bonjour,

Pendant que j'y suis, voilà le corrigé.
1. Plus avantageux = bénéfice supérieur
Vente de 7000 articles = 8,5*7000 = 59500 €
Coût de Production [tex]0.5\times 7^2+7+10,72 =42,22[/tex] milliers d'€ Soit [tex]C(7)=42220[/tex] €
Bénéfice : [tex]59500 - 42220 = 17280 €[/tex]

Vente de 9000 articles = 8,5*9000 = 76500 €
Coût de Production [tex]0.5\times 9^2+9+10,72 =60,22[/tex] milliers d'€ Soit [tex]C(9)=60220[/tex] €
Bénéfice : [tex]76500 - 60220 = 16280 €[/tex]
Il est plus avantageux fe fabriquer et vendre 7000 articles que 9000.

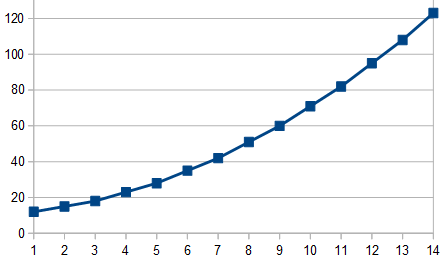
2. Tableau de valeurs

      x (milliers d'articles)      1   2   3   4   5   6   7   8   9  10  11  12  13   14
     C(x) (milliers d'euros)      12  15  18  23  28  35  42  51  60  71  82  95 108  123

courbe basée sur le tableau de valeurs arrondies

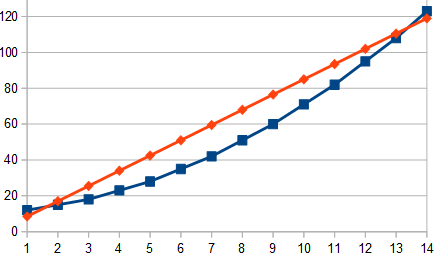
3. a)
Recette mensuelle avec x en milliers d'articles et R(x) en milliers d'euros (en vert).
[tex] R(x)=8,5x[/tex]
Courbes avec C(x) arrondi

Courbes réelles

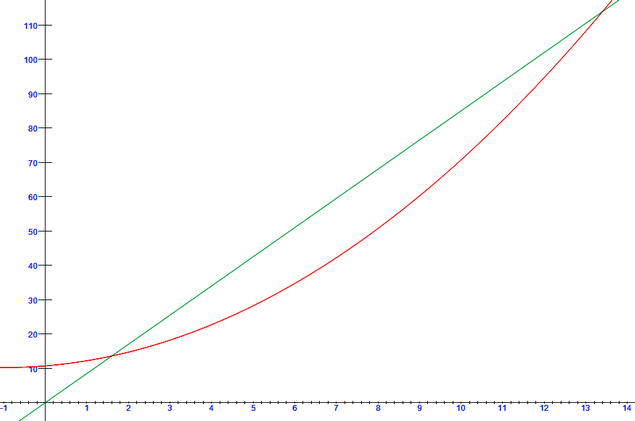
b) Bénéfice positif = Recettes > coûts soit R(x) > C(x)
graphiquement le droite représentative des variations de R au-dessus de la courbe (c)
On doit donc avoir [tex]x \in [2\,;\,13][/tex]
4. a) [tex]B(x)=8,5x -(0,5x^2+x+10,72)=8,5x -0,5x^2-x-10,72 = -0,5x^2+7,5x-10,72[/tex]
b) B(x) est un trinôme du 2nd degré : ax²+bx+c. Il est du signe de a à l'extérieur des racines et du signe de -a entre les racines, si elles existent.
[tex] \Delta = 7,5^2-4\times 0,5\times 10,72 = 35,71[/tex] Discriminant positif. Il y a deux racines.
[tex]x_1,x_2=\frac{-7.5\pm\sqrt{35,71}}{-1}\approx 1,52 \text{ et }13,48[/tex]
Soit pour ce qui concerne l'exercice : B(x) positif pour [tex]x \in[1,52\,;\,13,48][/tex] négatif pour [tex]x \in [0\;,1,52]\cup]13,48\,;\,14][/tex]
Si on ne sait pas encore utiliser le discriminant on peut s'en sortir sans :
[tex] B(x)=R(x)-C(x)[/tex]
Pour une valeur a de x donnée R(a), C(a) sont les ordonnées des points des courbe (r) et (c) d'abscisse a.
La différence R(a)-C(a) de ces ordonnées est B(a). Le bénéfice B(a) est positif si [tex]R(a)-C(a)>0[/tex], donc si [tex]R(a)>C(a)[/tex] donc pour les points où la droite (r) est au-dessus de la courbe (c) : on l'a déterminé graphiquement : pour [tex]x \in [2\,;\,13][/tex]

On sait depuis la 2nde que comme dans B(x) le coefficient de x² est <0 la fonction B est d'abord croissante passe par un maximum puis décroit (comme le symbole d'intersection).
Si ce coefficient est positif B (courbe en forme de U) est décroissante passe par un minimum et croît...

     x         0   1    2   xmax    13     14
                        |            |             
signe B(x)         -   2,3    +     2,3   -
                             max
                         /        \
                        /           \
variation             2,3            2,3
                     /                   \
                   /                       \

Les vrais beaux tableaux seraient (avec connaissance discriminant et dérivée) :

x    |0     1.52     2            13   13.48   14|
-----|-------|---------------------------|-------|
B(x) |   -   0            +              0   -   |

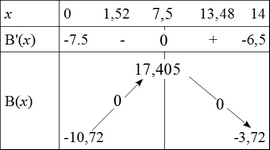
d)Si l'on sait ce qu'est une dérivée
[tex]B'(x)=-x+7,5[/tex]
On sait que B'(x) est croissant jusqu'à x=7,5 décroissant ensuite et que le maximum est atteint pour x=7,5.
Si on ne sait pas, on a quand même appris en 2nde que le sommet de la parabole d'équation [tex]y=ax^2+bx+c[/tex] a pour abscisse [tex]x=-\dfrac{b}{2a}[/tex], ici [tex]x = -\dfrac{7,5}{-1}=7,5[/tex]
Le bénéfice pour x=7.5 milliers d(objets fabriqués et vendus sera : [tex]-0.5\times 7.5^2+7.5\times 7.5-10.72 = 0.5 \times 7.5^2-10,72=17.405[/tex] k€...
soit 17405 €

@+

Forum de mathématiques - Bibm@th.net

#1 17-02-2018 21:00:41

Second degré

#2 17-02-2018 22:39:12

Re : Second degré

#3 17-02-2018 23:34:40

Re : Second degré

#4 18-02-2018 11:07:58

Re : Second degré

#5 18-02-2018 12:12:42

Re : Second degré

#6 19-02-2018 19:35:30

Re : Second degré

Pied de page des forums