Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 22-09-2017 16:16:23
- leo0
- Membre
- Inscription : 18-09-2017
- Messages : 266
Calculer une aire avec Geogebra
Bonjour
Pouvez vous m'aidez pour ce devoir de Géométrie ( qui n'est pas noté ) s'il vous plait ?
ABCD un carré de coté 2
On note I et J les milieux des cotés [AD] et [DC]
On place un point I mobile sur le segment [IJ] , on construit le triangle ABM
On note H le pied de la hauteur issue de M dans ce triangle
On pose AH = x
1 - Justifier que MH = 1 + x
2 - Indiquer ou doit on placer M pour que l'aire du triangle AMB soit égale à un tiers de l'aire du carré
--------------------------------------------------------------------------
Pour la Construction de la figure
--------------------------------------------------------------------------`
Avec Géogébra, j'ai placé les points A,B, C et D avec l'outil point
puis j'ai tracé les segments [AD] et [DC]
pour les milieux de [AD] et de [DC], en utilisant l'outil milieu et centre ( dessin de trois points alignés en diagonale)
j'ai sélectionné le point A puis le point B pour avoir le point I milieu de [AD]
meme chose pour obtenir le point J
Pour la hauteur [MH], j'ai utilisé l'outil point et j'ai cliqué un point en dessous de M sur [AB]
Le professeur nous a demandé :
- faire émerger les éléments mobiles et variables et les éléments fixes et constants de la figure puis introduire le point I' si nécessaire
- définir un lien fonctionnel entre les variables
Les sommets A et D sont fixes donc [AD] aussi
AH = x ---> x ne peut varier que de 0 à 1 puisque M varie de I a J
Hors ligne
#2 22-09-2017 16:19:33
- leo0
- Membre
- Inscription : 18-09-2017
- Messages : 266
Re : Calculer une aire avec Geogebra
c'est encore moi
j'ai fait une figure mais je n'ai pas trouvé la pièce jointe
Hors ligne
#3 22-09-2017 19:26:55
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Calculer une aire avec Geogebra
Bonjour "encore toi",
Il n'y a pas possibilité de pîèce jointe.
Le plus simple est de déposer ton image sur http://www.cjoint.com qui va te donner une adresse à coller dans un nouveau post.
Bon, j'ai fait le dessin (Moi, je l'ai mis sur casimages.com) : quel est ton problème dans ce devoir ?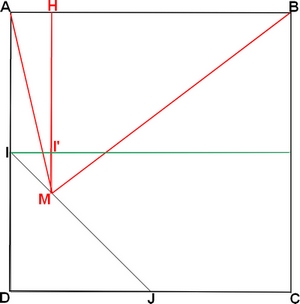
Alors trace la parallèle à (AB) passant par I : elle coupe [MH] en I' :
MH = MI' + I'H.
A toi de jouer...
Question 2.
L'aire du carré est 4, donc tu cherches à placer M pour que l'aire du triangle AMB vale [tex]\frac 4 3[/tex]...
Quelle doit donc être la mesure de MH ?
Or tu sais que MH = 1+x.
Quelle est donc la valeur de x (fraction de numérateur 1).
Si tu veux placer avec précision le point H, il va te falloir tracer des parallèles équidistantes pour partager {AN], N étant le milieu de [AB en le nombre voulu de parties...
Je ne te dis pas tout.
Reviens si nécessaire...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#4 22-09-2017 19:56:23
- leo0
- Membre
- Inscription : 18-09-2017
- Messages : 266
Re : Calculer une aire avec Geogebra
bonsoir Yoshi
MH = 1 + x
donc
MH -1 = x
fraction de numérateur 1 ( je ne vois pas )
s'il te plait : ne me donne pas la réponse tout de suite ( j'aimerais trouver tout seul )
Hors ligne
#5 22-09-2017 20:28:38
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Calculer une aire avec Geogebra
Re,
MH = 1 + x
donc
MH -1 = x
Ça ne ne te mènera pas à la solution, désolé !
Tu ne crois pas que tu devrais utiliser AH ?
(cliquer sur la légende pour déplier)
@+
[EDIT]
J'arrête là.
RdV demain...
Dernière modification par yoshi (22-09-2017 20:56:26)
Arx Tarpeia Capitoli proxima...
Hors ligne
#6 22-09-2017 21:49:09
- leo0
- Membre
- Inscription : 18-09-2017
- Messages : 266
Re : Calculer une aire avec Geogebra
Bonsoir
Dans l'énoncé on ne parle pas de droite parallèle passant par I
Le but de tracer une parallèle à [AB] passant par I
c'est pour démontrer que [AI] = [HI'] ??
Hors ligne
#7 23-09-2017 07:10:27
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Calculer une aire avec Geogebra
Bonjour,
Dans l'énoncé on ne parle pas de droite parallèle passant par I
C'est vrai : il n'évoque aucune parallèle du tout.
En plus, il parle d'un point I' qui arrive là comme un cheveu sur la soupe sans dire où il est...
Ce qui n'est pas normal : ton énoncé est incomplet.
De plus, toi tu écris :
On place un point I mobile sur le segment [IJ] , on construit le triangle ABM
T'es-tu relu ? C'était M...
Pour répondre à ta question (c'est oui), on te dit de montrer que MH = 1+x...
Avec ma parallèle, je coupe MH en I' :
MH = MI'+I'H.
Normalement, tu dois voir de MI' ou de I'H est égal à 1 et pourquoi et qui mesure x : c'est pour x que ça se corse un peu, d'où les pistes que je t'ai données hier soir en spoiler...
Fraction de dénominateur 1.
Tu ne vois pas ?
L'aire du carré est 4.
Quelle est doit être l'aire du triangle (que dit l'énoncé à ce sujet ?). C'est une fraction.
Comment calcule-t-on l'aire d'un triangle ?
Le côté ayant pour longueur 2, quelle est la valeur de MH ?
Et maintenant, tu peux écrire 1 + x = ...
Et tu vas en déduire x : fraction de dénominateur 1.
Construction de M pas évidente pour vous : il faut avoir un certain vécu...
Allez, au taf ! ^-^
@+
[EDIT] Où est censé être situé ce point I' ?
Parce que je peux aussi le placer entre I et D De façon à ce que (MI') soit perpendiculaire à (AD) : c'est même plus simple comme ça de prover que MH = 1+x.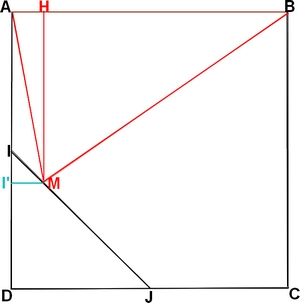
Donc où est-il ? Comme ci-dessus ?
Dans ce cas MH = AI' =AI+II'...
Il te resterait alors à évaluer II'
Dernière modification par yoshi (23-09-2017 09:15:51)
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1
Discussion fermée








