Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 07-08-2017 13:02:21
- charlène
- Invité
Etude de fonction
Bonjour à tous, je rencontre quelques soucis sur cet exercice et j'aurais besoin d'explications si possible
On considère la fonction f définie sur [1;4] par [tex]f(x)= \frac{x^3+2x^2}{x^2-1}[/tex]
1.Partie A
On considère la fonction g définie sur [1;4] par [tex]g(x)= x^3+x^2-7x-4[/tex]
a. Calculer g'(x) et faire le tableau de variation de g
b. Expliquer rapidement pourquoi l'équation g(x)=0 admet une solution unique alpha unique sur l'intervalle [1;4], puis déterminer une valeur approchée de alpha à 0.1 près à l'aide de la calculatrice.
c. En déduire le signe de g(x) sur [1;4]
2.Partie B
a. Calculer f'(x) et montrer que [tex]f'(x)= \frac{x.g(x)}{(x^2-1)^2}[/tex]
b. Etudier le signe de f'(x) et faire le tableau de variation de f
c. Vérifier que [tex] f(x)= x+2+\frac{x+2}{x^2-1}[/tex]
d. Etudier la position de la courbe C représentative de f par rapport à la droite D d'équation y=x+2
e. Tracer dans un repère orthogonal (O;i;j) (unités: 1cm sur l'axe des abscisses et 0.5cm sur l'axe des ordonnées) les droites d'équations [tex]x=-1[/tex]; [tex]x=1[/tex]; [tex]y=x+2[/tex] et la courbe C
Voici ce que j'ai fais:
Partie A:
[tex]a. g'(x)= 3x^2 +2x-7[/tex]
[tex]\Delta=2^2-4*3*(-7) =88[/tex]
Mes solutions sont donc à peu près -1.90 et 1.23. Cependant j'ai un peu de mal au niveau de mon tableau de variation
b. Je ne comprend pas cette question
c. Celle ci suit la a donc je ne peux pas y répondre pour le moment
Partie B:
a.Vient ici une complication. Voici ce que j'ai fais
(3x^2+4x)(x^2-1) - (2x)(x^3+2x^2)/(x^2-1)^2
ce qui fait que je trouve à la fin x(x^3-3x^2-4x)/(x^2-1)^2 or ce n'est pas le bon résultat et je ne comprend pas d'où peut provenir mon erreur
b. Je me suis perdue dans tous mes calculs, je sais que je dois partir de la question a mais le g(x) me bloque pour je ne sais qu'elle raison
c. Je trouve ici le bon résultat
d. Je n'y arrive pas
e. Je n'arrive pas à tracer mes courbes j'ai beaucoup de mal
Je ne demande pas les réponses je voudrais juste des explications pour me permettre de comprendre mes erreurs. Merci d'avance de vos réponses.
#2 07-08-2017 16:43:37
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Bonjour,
Partie 1
a)
Les solutions exactes de g'(x) sont [tex]\frac{-1\pm\sqrt{22}}{3}[/tex]
Tes valeurs approchées sont correctes.
g'(x) étant un polynôme du 2nd degré, son signe est celui de a à l'extérieur des racines, et de -a entre les racines.
Ici on a : a =3
Donc On a pour g'(x) : [tex] +\quad\;0\quad-\quad\;0\;\quad+[/tex]
Et g(x) est croissante, décroissante, croissante
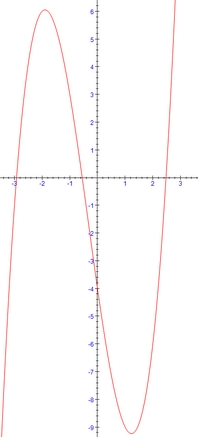
b)
Entre 1 et 4 il y a 2 et 3...
Sur le graphique ta solution unique tu vois qu'elle est comprise entre 2 et 3.
Par le calcul, tu constates g(2) <0 et g(3) >0 et sur [2 ; 3] g est croissante..
Alors ?
c) [tex]g(0)= -4[/tex]
[tex]\frac{-1-\sqrt{22}}{3}<0<1<\frac{-1+\sqrt{22}}{3}[/tex]
De [tex]\frac{-1-\sqrt{22}}{3}[/tex] à [tex]\frac{-1+\sqrt{22}}{3}[/tex] la fonction g est décroissante .
Puisque [tex]g(0) = -4 <0[/tex] qu'est-ce que tu conclus pour [tex]g(1)[/tex] ? pour [tex]g\left(\frac{-1+\sqrt{22}}{3}\right)?[/tex] ?
De [tex]\frac{-1+\sqrt{22}}{3}[/tex] à [tex]+\infty[/tex], g est croissante.
Or [tex]g(\alpha)=0[/tex] et [tex]\frac{-1+\sqrt{22}}{3}<\alpha[/tex]
Tu as tout ce qu'il te faut pour justifier les signes de [tex]g(x)[/tex] sur ]1 ; 4[
Partie 2
Il y a effectivement un prblème. Vérifie ton énoncé.
[tex]f(x)=\frac{x^3+2x^2}{x^2-1}[/tex]
Je pose [tex]U = x^3+2x^2[/tex] d'où [tex]U'= 3x^2+4x[/tex]
Je pose [tex]V = x^2-1[/tex] d'où [tex]V' =2x[/tex]
[tex]f'(x)=\frac{(3x^2+4x)(x^2-1)-(x^3+2x^2)(2x)}{x^2-1}[/tex]
Soit :
[tex]f'(x)=\frac{3x^4+4x^3-3x^2-4x-2x^4+4x^3}{(x^2-1)^2}[/tex]
Enfin :
[tex]f'(x)=\frac{x^4-3x^2-4x}{(x^2-1)^2}[/tex]
Or,
[tex]x.g(x)= x^4+x^3-7x^2-4x[/tex]
Ça ne colle pas.
Et pourtant les calculs sont justes.
Peut-être as-tu mal noté le g(x) ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 07-08-2017 17:02:04
- CHARLENE
- Invité
Re : Etude de fonction
Bonjour pour la partie 1 b je comprend ce que tu veux dire mais je ne vois pas comment l'expliquer
pour la partie 2 non la fonction g est bien celle que j'ai donner j'ai vérifier plusieurs fois c'est d'ailleurs pour cela que je ne comprend pas pourquoi je ne trouve pas le résultat qu'il faut car je trouve exactement comme toi
#4 07-08-2017 17:55:02
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Salut,
entretemps, j'ai utilisé un logiciel qui calcule ça : il est d'accord avec nous...
Rideau, on ne peut pas faire grand chose, sauf à supposer qu'il y a eu une erreur dans l'expression de g(x) et refaire la partie 1 comme si on nous avait donné la bonne expression [tex]g(x)=x^3-3x-4[/tex] dont la courbe représentative est la suivante :
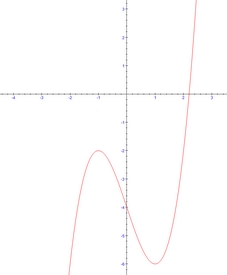
puis continuer la Partie 2...
1.b) C'est le théorème des "gendarmes"...
Il faut montrer que pour une certaine valeur a de x, [tex]g(a)<0[/tex] et que pour une certaine valeur b de x, [tex]g(b)>0[/tex].
Alors, on pourrait s'arrêter là et dire : pour passer d'une valeur négative de g(x) à une valeur positive on passe par une valeur [tex]\alpha[/tex] telle que [tex]g(\alpha)=0[/tex] et ce serait faux parce que pas toujours vrai :
il faut ajouter en plus que dur {a ; b] g est toujours soit croissante soit décroissante : ainsi on est sûr qu'il n'y a pas de changement de courbure et que [tex]\alpha[/tex] est bien unique...
C'est mieux comme ça ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 07-08-2017 18:13:32
- charlène
- Invité
Re : Etude de fonction
Bonjour, je comprend un peu mieux mais toujours pas au point de pouvoir me lancer et y répondre toute seule
Pour la partie 1 je vais tout refaire en prenant compte de l'erreur, merci
#6 09-08-2017 17:50:04
- charlène
- Invité
Re : Etude de fonction
Bonjour, je reviens vers toi parce que j'ai énormément de mal à construire mes tableaux de variations pour la question a de la partie A, b et d de la partie B
Pour le a je trouve g'(x) : + - + or ce n'est pas sur l'intervalle [1;4] mais -l'infini x1 x2 + l'infini et cela me bloque car je ne peut pas en déduire le signe sur l'intervalle qu'il faut, je ne sais pas si tu vois ce que je veux dire
Pour les autres mon problème est aussi ici car je n'arrive pas à me mettre sur le bon intervalle ce qui fait que cela me bloque
#7 09-08-2017 21:08:14
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Re,
Rapidement...
Mais si tu peux
[tex]g'(x)= 3x^2-3=3(x^2-1)=3(x-1)(x+1)[/tex]
x |-oo -1 1 +oo |
g'(x) | + 0 - 0 + |
| /-2 \ /+oo
g(x) | / \ /
______| -oo/ \-6 /
Tu vois bien que g'(x) est + entre 1 et +oo ... 4 est bien dans cet intervalle non ? donc g'(x) signe + entre 1 et 4.
Donc g est croissante entre 1 et 4
[tex]g(1)=-6[/tex] et [tex]g(4)=48[/tex]
Quel nombre particulier trouve-t-on une seule fois entre [tex]g(1)=-6[/tex] et [tex]g(4)=48[/tex] ? Et bien : [tex]g(\alpha)=0[/tex]
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 10-08-2017 11:13:54
- charlène
- Invité
Re : Etude de fonction
Bonjour, Oui d'accord je vois ce que tu as fais mais je me rend compte que comme ma fonction g(x) est du coup fausse ( soit maintenant x^3-3x-4), ma fonction g'(x) change donc et delta ne vaut plus 88 mais -3 ce qui me fais 1 racine au lieu de 2 ?
#9 10-08-2017 12:11:39
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Salut,
Oui, j'avais dit
Partie 2 infaisable si on ne modifie pas le [tex]g(x)[/tex] de la Partie 1. Prendre [tex]g(x)=x^3-3x-4[/tex]
Tu avais dit : d'accord, je refais tout !
M'enfin, relis-moi donc :
[tex] g'(x)= 3x^2-3=3(x^2-1)=3(x-1)(x+1)[/tex], solutions -1 et 1.
1. Pas besoin du [tex]\Delta[/tex], voir la factorisation ci-dessus.
2. Si tu y tiens absolument : [tex]\Delta = 0^2-4\times 3 \times (-3)=36=6^2[/tex]
[tex]x_1,x_2=\frac{0\pm 6}{6}=\pm 1[/tex]
Tout ça, alors qu'avec une factorisation niveau 3e, on arrive au même point.
3. Le discriminant ne se calcule qu'avec des polynômes du 2nd degré : c'est bien le cas du nouveau [tex]g'(x)[/tex], non ?
Un [tex]\Delta[/tex] de -3 ? Comment as-tu fait tes calculs ? La tu trouves un discriminant négatif : pas de solutions, ce qui est faux !
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#10 10-08-2017 12:23:01
- charlène
- Invité
Re : Etude de fonction
Non oui tu as raison je me suis trompée dans mon calcul
Comme tu le disais la dernière fois f'(x) est du signe de g(x) donc mon tableau est le même alors ?
#11 10-08-2017 13:05:29
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Re,
Comme tu le disais la dernière fois f'(x) est du signe de g(x) donc mon tableau est le même alors ?
Atta... Pas si vite...
Moi, je ne crois pas avoir écris ça !
[tex]f(x)=\frac{x^3+2x^2}{x^2-1}[/tex]
Et tu dois montrer que [tex]f'(x)=\frac{x.g(x)}{(x^2-1)^2}[/tex]
Donc, il te faut déjà le signe de [tex]g(x)[/tex] pour commencer...
Quel est donc ce signe ?...
[tex]g(x)[/tex] s'annule pour [tex]\alpha \in[1\,;\,4][/tex]
Sachant que la fonction g est croissante que [tex]g(1)=-6[/tex] et [tex]g(4)=48[/tex] quel est donc le signe de [tex]g(x)[/tex] ?
Ensuite le dénominateur est un carré : [tex](x^2-1)^2=(x-1)^2(x+1)^2[/tex], toujours de signe +, sauf que la valeur 1 est une valeur interdite,
Donc f'(1) n'existe pas !. Tu parleras donc du signe de [tex]f'(x)[/tex] sur [tex]]1\,;\,4][/tex] et non plus sur [tex][1\,;\,4][/tex]...
Enfin sur [tex][1\,;\,4][/tex], x est toujours +...
Donc sur cet intervalle, le signe de[tex] f'(x)[/tex] est le même que celui de [tex]g(x)[/tex]
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#12 10-08-2017 13:25:35
- charlène
- Invité
Re : Etude de fonction
g(x) est positif puis négatif puis positif comme f'(x), non ?
je trouve donc que sur -l'infini -1 c'est négatif, positif de -1 à 1 et re positif de 1 à +l'infini ? Soit f'(x) est positif sur l'intervalle ]1;4] et ses variations sont décroissante croissante croissante ?
#13 10-08-2017 14:24:51
- CHARLENE
- Invité
Re : Etude de fonction
Après rectification je trouve:
positif de -l'infini à 0 négatif de 0 à alpha et positif de 1 à +l'infini ce qui me fait croissante, croissante,décroit,décroissante,croissante donc ce qui fait que C est en dessous de D sur ]1,alpha] alors que C est au dessus de D sur [alpha;4] ?
#14 10-08-2017 18:30:18
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Bonsoir
ce n'est pas comme ça comme ça que l'on fait
On sait que [tex]f(x)= x+2+\frac{x+2}{x^2-1}[/tex] et que son asymptote oblique (D) a pour équation [tex]y =x+2[/tex]...
Soit [tex]h(x)=x+2[/tex]
Cf étant la courbe représentative de f, pour savoir si Cf est au dessus ou au dessous de son asymptote (et pour quel x), on regarde le signe de
f(x)-h(x) soit le signe de [tex]\frac{x+2}{x^2-1}=\frac{x+2}{(x-1)(x+1)}[/tex]
Tableau de signes obligatoire !
Si ton expression est >0 alors f(x)-h(x)>0 et donc f(x)>h(x), Cf au dessus de (D)... si <0 la courbe est en dessous.
Le tableau de variations que je t'ai proposé est à faire au brouillon : au propre, on ne donne que la zone comprise dans l'intervalle [tex][1\,;\,4][/tex] puisque l'énoncé définit expressément les différentes fonctions sur cet intervalle...
En conséquence tu établis au brouillon un tableau de signes complet, puis tu le restreins à l'intervalle donné [tex][1\,;\,4][/tex]
L'énoncé est vraiment mal écrit.
J'y trouve :
e) Tracer dans un repère orthogonal (O;i;j) (unités: 1cm sur l'axe des abscisses et 0.5cm sur l'axe des ordonnées) les droites d'équations [tex]x=−1[/tex] ; [tex]x=1[/tex] ; [tex]y=x+2[/tex] et la courbe C
Pour quoi faire tracer la droite x = -1 puisque la fonction f n'est à étudier que sur [tex][1\,;\,4][/tex] et donc Cf à tracer seulement pour [tex]x\in [1\,;\,4][/tex]...
Ce n'est donc pas logique ; soit on travaille sur [tex][-\infty\,;\,+\infty][/tex] soit sur [tex][1\,;\,4][/tex] : il faudrait savoir ce qu'on veut...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#15 10-08-2017 18:47:05
- charlène
- Invité
Re : Etude de fonction
Bonsoir, merci pour tes explications j'ai pu faire mon tableau de variation
pour tracer le repère, c'est pourtant ce qu'il y a écrit dans mon énoncé cependant, il y a t-il une technique pour pouvoir savoir comment tracer ses droites ? Parce que je n'ai jamais compris comment faire
#16 10-08-2017 20:25:39
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Salut,
Que ce soit une droite ou une courbe, il te faut des points...
Pour une droite deux points suffissent.
Tu prends deux abscisses quelconques (enfin qui ne te donnent pas trop de calculs et faciles à placer) puis tu calcules l'ordonnée des points de cette droite ayant ces abscisses...
Pour y = x+2, je choisis par exemple x = -5 et x = 6 (donc assez éloignés de préférence : le tracé n'en sera que plus précis)
x = -5 --> y=-5+2= -3 soit le point [tex] (-5\,;\,-3)[/tex]
x = 6 --> y =6+2 = 8 soit le point [tex] (6\,;\,8)[/tex]
Tu places tes deux points et tu traces ta droite.
Demain je te donnerai mon tableau de variations pour voir si c'est juste...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#17 10-08-2017 20:49:06
- charlène
- Invité
Re : Etude de fonction
Ah d'accord j'ai compris merci beaucoup, du coup comme tu disais que tracer x= -1 ne servait à rien, il faut que je le mette quand même tu penses ou cela ne servirait pas à grand chose ?
D'accord sa marche merci
#18 12-08-2017 20:51:19
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Salut,
La fin de la partie 2 était sans commune mesure avec la partie 1...
Ce n'était pas si simple que ça...
D'abord [tex]g'(x)[/tex]
Signe de g'(x) :
g'(x) + 0 - 0 +
D'où variations de g :
g'(x) + 0 - 0 +
g(x) /-2 \ /+oo
/ \ /
-oo/ \-6 /
Signe de g(x)
Sur [tex] ]-\infty\,;\;1[[/tex] g(x) est négatif
Sur [tex] ]1\,;\;+\infty[[/tex] g(x) croît de 6 à +oo : il passe par 0 pour [tex]x =\alpha \approx 2.195801[/tex]
Donc, en fait : sur [tex]]-\infty\,;\;\alpha[[/tex] g(x) est négatif, et positif ensuite...
Tout ça pour quoi faire ?
Mais pour trouver le signe de [tex]f('x)=\frac{x.g(x)}{(x^2-1}[/tex] !!!
Le signe de f'(x) est celui du numérateur, puisque le dénominateur est toujours positif... ou nul !
Alors même si le signe du dénominateur n'intervient pas, il faut quand même tenir des valeurs interdites -1 et + 1 que je dois placer dans mon tableau :
x - | - 0 + | + | +
g(x) - | - | - | - | +
----------------|-----|-----|-----|-----------
x.g(x) + | + 0 - | - 0 +
Et maintenant f'(x) et f(x)
--------------||------|----||-------|--------------
f'(x) + || + 0 - || - 0 +
--------------||------|----||-------|--------------
/+oo|| /0\ ||+oo\ /+oo
f(x) / || / \ || \ /
-oo/ ||-oo/ -oo\ || \5,28/
Et tu vois bien que pour t'en sortir et ne donner que la portion [tex]]1\,;\;4[[/tex], il fallait bien tout faire au brouillon...
Quant à ta courbe complète, la voilà, avec les asymptotes :
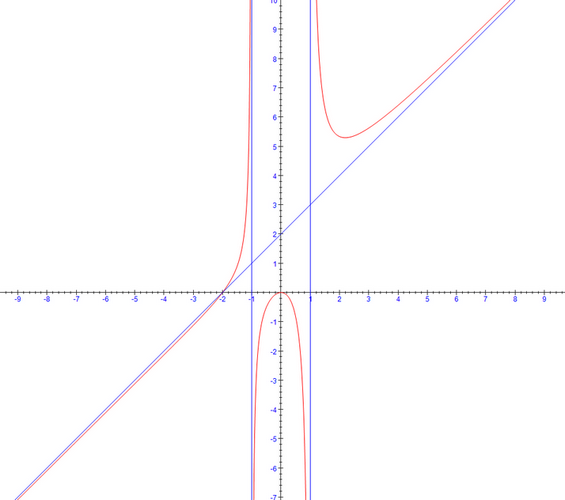
Tout compris ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#19 13-08-2017 15:13:46
- charlene
- Invité
Re : Etude de fonction
Bonjour, Oui j'ai tout bien compris c'est ce que je trouvais aussi, juste pour la courbe, pour que tout sois précis il faut que je prenne des points c'est ça ? Merci beaucoup pour ton aide
#20 13-08-2017 17:59:01
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude de fonction
Re,
il faut que je prenne des points c'est ça ?
Si on veut tracer l'intégralité de la courbe, il vaut mieux en prendre 5 ou 6 par zone...
C'est là qu'on apprécie la calculette graphique pour savoir ce que l'on fait...
Si tu as fait la même chose, alors bravo !
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#21 13-08-2017 21:06:22
- charlène
- Invité
Re : Etude de fonction
Bonjour, oui je vais prendre plusieurs points alors pour être vraiment précise, merci beaucoup pour ton aide !
Pages : 1
Discussion fermée








