Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 12-07-2017 13:01:00
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Démonstration du théorème de Pythagore .
Bonjour
Voici une démonstration que j'ai faite il y a plus de 20 ans .
Prenons un triangle rectangle a b c . Tirons de ce triangle un triangle semblable mais de hauteur 1 . Les trois côtés prennent une autre identité :
Côté opposé = c/b
Côté adjacent = c/a
Hypothenuse = ( a/b ) + ( b/a )
On admet que la hauteur h = ( a * b ) / c
On a donc : ((c/a) * (c/b)) / ((a/b) + (b/a)) = 1
Donc : a**2 + b**2 = c**2
Cette démonstration diffère des autres car elle n'a pas recours à la géométrie .
Hors ligne
#2 12-07-2017 16:04:06
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Bonjour,
Bienvenue chez nous...
Éclaircissons ton énoncé :
* ton triangle rectangle ABC est-il d'hypoténuse [BC] ?
(tiens, tu me rappelles, qu'en 2nde, j'avais copié 50 fois : hypoténuse ne prend pas de h après le t... ^-^)
Et tu notes bien BC =a, AB =c et AC = b ?
* côté opposé et côté adjacent ? Moi, j'ai l'habitude d'utiliser ces adjectifs relativement à un angle. Alors lequel ?
Toi, c'est par rapport à un sommet ? Si oui, lequel ?
* On admet que la hauteur h = ( a * b ) / c je ne te suis plus ? Tu as commencé par dire que h = 1... Donc a*b/c=1 ?
D'autre part la présence dans une démonstration de "on admet que" me gène beaucoup... Tu l'admets parce que tu nous fais grâce de la démo pour ne pas trop rallonger la sauce ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 12-07-2017 16:18:03
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Bonjour
Il est vrai que l'énoncé est assez mal rédigé . Il aurait fallu pour cela que je puisses vous faire voir une Illustration .
Le gros problème réside dans l'ancienneté de cette démonstration et j'avoue , à défaut de vouloir la surcharger , me souvenir avec peine des détails
de cette démonstration .
Dois-je recopier 50 fois qu'hypotenuse n'a pas de h après le t ( ce serait mérité)
Hors ligne
#4 12-07-2017 16:35:26
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Salut,
Il est vrai que l'énoncé est assez mal rédigé . Il aurait fallu pour cela que je puisses vous faire voir une Illustration .
Pour mettre une image sur le forum (pas un "drap de lit", hein..)
1. Faire ton dessin et le stocker au format .jpg ou .png sur ton disque dur ou un support quelconque
2. Connecte-toi à un hébergeur (gratuit) d'images : casimages.com, photobucket, hiboox, noelshack...
3. Va chercher ton image dans le dossier où tu l'as mise, sélectionne le nom du fichier et envoie-le (on appelle ça uploader)
4. Tu vas récupérer un code entre balises[ img] et [ /img], tu le colles dans ton post...
Si ça te paraît compliqué, autre solution à partir du point 2. :
2. Connecte-toi à www.cjoint.com suis les instructions pour un hébergement temporaire...
3. Tu récupères le code fourni et le le colles dans un post.
4. Je récupère ton image, et je la dépose chez casimages et je modifie le code de ton post : ton image sera alors directement visible par tous..
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 12-07-2017 16:37:03
- Yassine
- Membre
- Inscription : 09-04-2013
- Messages : 1 090
Re : Démonstration du théorème de Pythagore .
@Yoshi,
Je suis tombé sur quelques posts d'Alain Ratomahenina sur un autre site.
Le contenu est à peu de choses près le même : il revient sur un résultat ancien et s'en attribue la paternité
Extraction de racine
Racine de 2 n'est pas irrationnel !
Gauss est un vantard
Couper les cheveuxcarrés en 4
L'ennui dans ce monde c'est que les idiots sont sûrs d'eux et les gens sensés pleins de doutes. B. Russel
Hors ligne
#6 12-07-2017 16:57:07
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
À Yassine
J'ai effectué les opérations voici le code : http://www.cjoint.com/c/GGmo1qesXzR
Hors ligne
#7 12-07-2017 17:11:19
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Voici donc l'illustration , merci à Yoschi .
Là , vous avez tout sous les yeux sauf qu'il faudrait que je puisses démontrer les identités des côtés du triangle de hauteur 1 et la formule exprimant la hauteur . À l'époque , je disposais d'"outils" intellectuels que je n'ais plus maintenant .... Mais peut être que vous y arriverez d'après les éléments .
Hors ligne
#8 12-07-2017 18:15:49
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
SRe,
Bon et bien, c'était bien le dessin auquel j'étais arrivé...
Quant à le décrire, ce n'était quand même pas la mer à boire, l'ami :
Ce qui conçoit bien s'énonce clairement
Et les mots pour le dire arrivent aisément.
a dit Nicolas Boileau...
Donc, j'ai refait ton truc parce que la couleur de fond rose ne sert à rien, et l'image elle-même n'a pas besoin d'être une image "couleur"...
En posant C'H = h'=1.
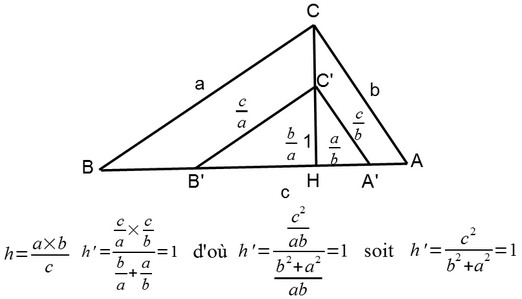
Quant à :
[tex]1+2+3+4+....+n = \frac{n ( n + 1 )}{2}[/tex]
Vous connaissez sûrement cette petite formule que l'on retrouve dans Wikipédia . On ne sait pas qui a trouvé cette formule ; Eh bien C'est moi, Alain Ratomahenina
faut pas pousser le bouchon trop loin, camarade : cette formule qui figurait dans mon livre de Maths d'Arithmétique lorsque j'ai passé mon Bac Mathématiques Elementaires en juin... 1966.
Au mieux tu l'avais [tex]RE[/tex]-trouvée !
Concernant son auteur, tu as mal lu Wikipedia, parce que moi, j'y lis :
Srinivasa Ramanujan présente deux démonstrations de « 1 + 2 + 3 + 4 + ⋯ = −1/12 » au chapitre 8 de son premier carnet. Et aussi
Srinivâsa Aiyangâr Râmânujan né le 22 décembre 1887 à Erode et mort le 26 avril 1920 à Kumbakonam, est un mathématicien indien.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 12-07-2017 18:29:18
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
@Yoshi
Oui en effet j'en ais bien honte , 1+2+3+n était connu bien avant moi , mais l'école m'a fait croire que j'en étais à l'origine : savez vous que d'après eux , cette formule , et le professeur nous l'a démontré , à servi à élaborer les fonctions primitives ? Se sont Ils moqué de moi à ce point ?
Hors ligne
#10 12-07-2017 19:04:27
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
RE,
Pour la justesse de la chose, il faut inverser les points A et B ce qui n'est pas conventionnel...
La demo n'est que du niveau 3e, chapitre Théorème de Thalès, Réduction/agrandissement.
Ici réduction : A'B'C' est une réduction de ABC de coefficient [tex]k = \frac 1 h = \frac{c}{ab}[/tex]
[tex]A'C' = k.AC[/tex] d'où [tex]b'= b\times \frac{c}{ab}= \frac c a[/tex]
[tex]B'C' = k.BC[/tex] d'où [tex]a'= a\times \frac{c}{ab}= \frac c b[/tex]
Problème....
Pourquoi n'as-tu pas placé les points A,B,C sur ton dessin ?
Pour la suite, si je traite A'B' directement à partir de AB et k je tombe ensuite sur 1 = 1... Brillant résultat !
Donc effectivement, il faut calculer B'H à partir de BH et k, puis A'H à partir de AH et k...
Donc on part de la formule
[tex]BC^2=BH.BA[/tex] qui dérive du fait que ABC, HBA, et HAC sont des triangles semblables et non de Pythagore, ouf !
[tex]BH = \frac{a^2}{c}[/tex] d'ou [tex]B'H = BH\times k = \frac{a^2}{c}\times \frac{c}{ab}=\frac a b[/tex]
Quant à AH on montrerait de même que [tex]AH = \frac b a[/tex]
Voilà pour la démonstration, même si les valeurs calculées ne sont pas affectées aux mêmes côtés...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#11 12-07-2017 19:59:44
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Je remarque que Yoshi à utilisé la formule de la hauteur pour déterminer c/à et c/b . En fait cette relation exprimerait des surfaces : a*b = h*c . Ce système peut être intéressant pour identifier des formes complexes .
Hors ligne
#12 13-07-2017 09:27:49
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Bonjour,
Je remarque que Yoshi a utilisé la formule de la hauteur pour déterminer c/a et c/b . En fait cette relation exprimerait des surfaces : a*b = h*c
Explication de texte.
Il serait plus juste de dire que cette relation proviendrait de l'expression de l'aire du triangle ABC de 2 façons :
[tex]\frac {ch}{2}=\frac{ab}{2}[/tex] d'où on tire [tex]ch = ab[/tex].
On peut tirer également cette égalité des rapports égaux exprimant que ABC, ACH et BCH sont des triangles semblables.
Ou encore que, de mon temps en 3e, on avait un chapitre de Géométrie qui s'appelait Relations métriques dans le triangle rectangle et dans lequel (en utilisant les notations du dessin) on trouvait :
[tex]BC^2=BH\times BA[/tex], [tex]AC^2=AH\times AB[/tex], [tex]CH\times AB = BC\times AC[/tex]
et que je n'ai fait qu'utiliser des théorèmes connus sans avoir réinventé la roue.
Ce système peut être intéressant pour identifier des formes complexes .
Si tu pouvais préciser ta pensée...
[tex]S=1+2+3+\cdots+n=\frac{n(n+1)}{2}[/tex]
savez vous que d'après eux , cette formule , et le professeur nous l'a démontré , à servi à élaborer les fonctions primitives ?
Moi, non, et je ne vois pas...
Ce ne serait pas : calcul de la valeur numérique entre deux bornes de l'intégrale d'une fonction ?
Explique !
Je ne demande qu'à m'instruire...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#13 13-07-2017 09:42:24
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
On voit que a*b peut être tout à fait quelconque de par sa forme ( triangle rectangle inscrit dans le demi cercle ) on sait que sa surface sera toujours égale à un rectangle
h * c qui lui ne varie que d'un côté . Le rectangle a * b peut "cadrer" une forme complexe et on en retrouve sa surface par le rectangle h * c . Il s'agit là de mesure qui pourrait être exploité en électronique par exemple .
Hors ligne
#14 13-07-2017 10:32:35
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
@yoshi
Quant à la formule de la somme des entiers consécutifs ceci remonte à trop loin ( + de 30 ans ) pour que je puisse t'en d'écrire la forme précise concernant les fonctions primitives . Mais il y a 1an , pour te dire l'histoire , j'étais cité en première page sur Google quand on lui demandait : Qui est à l'origine du calcul intégral ?
En fait , je ne sais pas grand chose sur cette histoire , surtout à quand remonte les fonctions primitives , Newton , Leibniz ?
Hors ligne
#15 13-07-2017 11:01:03
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Re,
On voit que a*b peut être tout à fait quelconque de par sa forme ( triangle rectangle inscrit dans le demi cercle ) on sait que sa surface sera toujours égale à un rectangle
Oh, mais cher ami, via coloriage découpage collage, je montrais à mes élèves de 6e, que la formule de calcul de l'aire d'un triangle quelconque, d'un parallélogramme, d'un losange ou d'un trapèze quelconque se retrouvait à partir de l'aire d'un rectangle...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#16 13-07-2017 11:45:43
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Voici un document qui permet d'observer le comportement du rectangle a * b et a' * b' à l'intérieur du cercle . Les dimensions a et b sont quelconques on aura la correspondance en h * c .
http://www.cjoint.com/c/GGnjLKBgCGR
Hors ligne
#17 13-07-2017 18:29:42
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Salut,
QQ explications sur ce que tu as bricolé seraient utiles :
point fixe ? rotation du rectangle ? etc...
Ensuite à partir de là, je peux te faire
- soit une animation automatique avec les outils dispos sur le site
- soit une image ouù on peut déplacer un point et tout le reste suit...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#18 13-07-2017 18:48:57
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Re
Dans ce schéma c , l'hypotenuse , est le diamètre . Les points fixes du trangle rectangle , demi rectangle ab ou a'b' , sont ceux de l'hypotenuse . L'angle droit de ces triangles parcourent la circonférence du cercle . La hauteur h du triangle rectangle correspond à un côté du rectangle ch .
Hors ligne
#19 16-07-2017 09:58:58
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Bonjour
Voici comment on détermine la hauteur h par rapport aux trois côtés a,b et c .
Hors ligne
#20 16-07-2017 11:23:15
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Démonstration du théorème de Pythagore .
Bonjour,
Donc d'après ta formule, un triangle équilatéral de coté 1 a une hauteur de 1?
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#21 16-07-2017 11:36:27
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Re
@Tibo , seulement si ce triangle est rectangle .
Hors ligne
#22 16-07-2017 12:20:52
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Démonstration du théorème de Pythagore .
Au temps pour moi, cette formule fonctionne pour calculer la hauteur perpendiculaire à l’hypoténuse dans un triangle rectangle .
Dernière modification par tibo (16-07-2017 12:22:08)
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#23 16-07-2017 12:57:51
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Démonstration du théorème de Pythagore .
Bonjour,
cette formule fonctionne pour calculer la hauteur perpendiculaire à l’hypoténuse dans un triangle rectangle
Bin vi... Mais pour les "anciens", elle n'a rien d'original, elle faisait partie intégrante, il y a un temps certain déjà, du chapitre "Relations métriques dans le triangle rectangle". Mais ce chapitre a fini par disparaître des programmes de 4e/3e...
Supposons hypoténuse [AB] et hauteur [CH].
L'égalité AC.BC = CH.AB était établie de 2 façons :
- Soit en remarquant que les triangles ACH, BCH et ABC sont semblables et en écrivant les rapports égaux qui en découlent.
- Soit en exprimant l'aire du triangle ABC
* en considérant le triangle comme un demi-rectangle : [tex]\frac{AC \times BC}{2}[/tex]
* en l'exprimant par la formule classique : [tex]\frac{\text{Base }\times\text{ hauteur}}{2}=\frac{AB\times CH}{2}[/tex]
et en égalant les deux expressions.
Les triangles semblables et les rapports égaux permettaient d'établir aussi que :
[tex]AC^2=AH\times AB[/tex] et [tex]BC^2 = BH\times BA[/tex]
Rien de bien neuf sous le soleil, donc...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#24 16-07-2017 13:08:46
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Re
Il faut avouer que bien que très simple mais pas forcément évidente , cette relation exprimant la hauteur d'un triangle rectangle n'est pas très populaire ....
Hors ligne
#25 16-07-2017 14:11:53
- Alain Ratomahenina
- Membre
- Inscription : 05-07-2017
- Messages : 25
Re : Démonstration du théorème de Pythagore .
Re
Que pensez-vous de mon " théorème " ?
En tout cas , il est vérifié pour le triangle equilateral .
Hors ligne








