Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 23-08-2016 10:25:34
- KypKool
- Invité
Cercle, triangle et fonctions
Bonjour,
Je suis en train de chercher à résoudre un problème de géométrie assez particulier qui me tient en haleine depuis quelques jours
Soit un demi-cercle dans le plan X,Z de rayon R et un point A sur ce demi-cercle.
L'angle entre le point P situé sur le centre et le point A avec l'axe X est l'angle alpha et xA est la projection de A sur l'axe des X.
Imaginons maintenant que je déplace le point P d'une distance de x sur l'axe X.
l'angle APX est maintenant alpha'.
Soit A' sur le cercle tel que A'CX soit égal à alpha' et xA' la projection de A' sur x et d le déplacement etre xA et xA'
Je cherche à exprime f(x)=d, j'ai l'intuition qu'il serait même plus judicieux de dire f(x/R)=d. Je pensais tout simplement que f serait atan mais cela n'est pas si simple que ça.
#2 23-08-2016 13:34:59
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Salut,
Intéressant, mais pas simple effectivement...
Puisque tu places P d'abord, je pense que c'est d tu feux exprimer en donc de x donc d = f(x).
Maintenant ton point P, va-t-il se cantonner à être à gauche de C iou pourra-t-il aussi aller de l'autre côté ?
Concernant le rayon, je pense, qu'on peut d'abord faire l' essai avec le cercle trigonométrique de rayon 1. après, on verra....
Je continue à chercher.
@+
[EDIT] ton point A déterminant l'angle [tex]\alpha[/tex] reste-t-il sur le quart de cercle de droite ? Le décrit-il intégralement ?
[EDIT2] J'ai refait un dessin autrement qu'à main levée :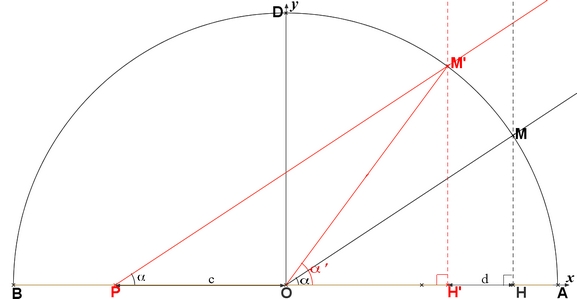
Maintenant ce sera plus facile de "causer".
Le point H' doit-il rester entre O et A ?
Si la réponse est oui, alors on a [tex]d= R(\cos\alpha-\cos\alpha')[/tex]
Si non, M doit-il rester toujours sur l'arc AD [tex]0\leqslant \alpha \leqslant \frac{\pi}{2}[/tex] ?
Si oui alors, pour [tex]\alpha\geqslant\frac{\pi}{4}[/tex], il y aura des positions de P pour lesquelles H' va se trouver entre O et B. C'est acceptable avec ta problématique ?
Dernière modification par yoshi (23-08-2016 21:26:28)
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 24-08-2016 12:25:30
- KypKool
- Invité
Re : Cercle, triangle et fonctions
Salut,
Merci pour cette réponse et ce beau schéma.
Je vais donc formuler mes précisions à partir de ton schéma.
- le point P peut être aussi bien à gauche ou à droite de C ainsi H est entre A et B. Mais pour simplifier comme le problème est symétrique nous pouvons rester sur la partie OA
- Une remarque dans ma formulation l'angle α ' n'est pas AOM mais APM et M' est positionné par l'angle α '. Dans cette formulation et dans ton schéma M' serait alors à une élévation plus basse que M.
Je pensais pouvoir exprimer f tq que f(x,R)=d mais en fait je pense que la fonction est f(x, α ,R) = d.
En effet le déplacement d est fonction de la position du point M de départ.
Pour un déplacement de P donné, un point M près de D donnera un d plus grand que pour un point M près de A
#4 24-08-2016 13:45:57
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Salut,
Ton problème est très complexe, c'est pourquoi je le coupe en tranches et j'essaierai de recoller les morceaux après (si j'y arrive !).
Alors, reprenons...
Voilà comment j'ai interprété tes dessins.
Sur un demi cercle de diamètre [AB] et de centre O, je définis un repère orthonormé (O ; x,y).
Sur la moitié droite de ce demi-cercle (donc dans le 1er quadrant) je place un point M : [tex]\widehat{AOM}=\alpha[/tex]. avec [tex]0< \alpha \leqslant \frac{\pi}{2}[/tex]
Sur le rayon [OB], je place un point P.
De P, je trace la parallèle à (OM) qui (lorsque c'est possible) coupe le demi-cercle en M'. Je joins [OM'].
Je note [tex]\widehat{AOM'}=\alpha'[/tex]
Puisque (PM') est parallèle à (OM), alors les angles correspondants [tex]\widehat{M'PA}[/tex] et [tex]\widehat{MOA}[/tex] sont égaux :
[tex]\widehat{M'PA}=\widehat{MOA}=\alpha[/tex]
j'abaisse les perpendiculaires de M' et M sur (AB) et j'obtiens les points H' et H. Tu notes d= HH'
Je note par [tex]x[/tex] l'abscisse de P : [tex]-R\leqslant x \leqslant 0[/tex]
Pour un angle [tex]\alpha[/tex] donné, je déplace P sur [OB] et je regarde l'évolution de d en fonction de la valeur de x.
J'ai réalisé le dessin avec le logiciel de Géométrie du site : GeoLabo. qui me permet des déplacements. Il est loin d'être aussi puissant que Geogebra, mais il va très bien pour ce que je veux voir...
En quoi es-tu en désaccord avec cette construction ? Pour moi, c'est strictement équivalent, à ce détail près, que partant de ton dessin 1 et donc d'un point M (A pour toi), par formation, si on en construit un deuxième à partir de P sur [OB], il est plus "naturel" de nommer ce second point M', plutôt que d'appeler ainsi celui est resté en place : il te suffit dans ce que je dis (ou sur le dessin) M et M', H et H',[tex] \alpha[/tex] et [tex]\alpha'[/tex]...
Avec mes conditions j'ai trouvé une formule, encore à re-vérifier qui exprime [tex]x[/tex] en fonction de [tex]R,\;\alpha,\;\alpha'[/tex].
J'avais tort, je ne peux pas faire l'impasse sur le rayon R et le ramener à 1.
@+
Dernière modification par yoshi (24-08-2016 16:24:45)
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 25-08-2016 13:37:43
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Bonjour,
a priori (je dois tester plus), ça devrait être bon, resterait à écrire d en fonction de x...
Donc, voilà la base du raisonnement :
Condition de colinéarité (y compris parallélisme) de 2 vecteurs [tex]\vec V(x\;;\;y)[/tex] et [tex]\vec V\,'(x'\;;\;y')[/tex] :
il existe [tex]k \in \mathbb{R}[/tex] tel que [tex]\vec V =k.\vec V\,'[/tex].
Autres formes
[tex]\frac{x}{x'}=\frac{y}{y'}[/tex] ou encore [tex]xy'-x'y = 0[/tex] : c'est cette dernière forme que je vais privilégier.
On a [tex]\overrightarrow{OM}(R\cos \alpha\;;\;R\sin \alpha)[/tex]
Et
[tex]\overrightarrow{PM'}=\overrightarrow{PO}+\overrightarrow{OM'}[/tex]
[tex]\overrightarrow{PO}(-x\;;\;0)[/tex] et [tex] \overrightarrow{OM'}(R\cos \alpha'\;;\;R\sin \alpha')[/tex]
Donc : [tex]\overrightarrow{PM'}(-x+R\cos\alpha'\;;\;R\sin\alpha')[/tex]
Avec
[tex]\overrightarrow{OM}(R\cos \alpha\;;\;R\sin \alpha)[/tex]
et
[tex]\overrightarrow{PM'}(-x+R\cos\alpha'\;;\;R\sin\alpha')[/tex]
ma condition de colinéarité s'écrit donc :
[tex]R\cos \alpha \times R\sin\alpha' - (-x+R\cos\alpha')\times R\sin \alpha = 0[/tex]
Et comme R est non nul je simplifie en :
[tex]R\cos \alpha \times \sin\alpha' - (-x+R\cos\alpha')\times\sin \alpha = 0[/tex]
Je développe :
[tex]R\cos \alpha \sin\alpha' +x\sin\alpha-R\cos\alpha'\sin \alpha=0[/tex]
j'isole x :
[tex]x\sin\alpha = R\cos\alpha'\sin \alpha-R\cos \alpha \sin\alpha'[/tex]
[tex]x\sin\alpha = R(\cos\alpha'\sin \alpha-\cos \alpha \sin\alpha')[/tex]
Ma parenthèse est la forme [tex]\sin a \cos b-\sin b \cos a[/tex] qui se contracte en [tex]\sin(a-b)[/tex]
J'ai donc :
[tex]x\sin\alpha = R\sin(\alpha-\alpha')[/tex]
Et enfin :
[tex]x = R\frac{\sin(\alpha-\alpha')}{\sin \alpha}[/tex]
Essai avec [tex]\alpha=\frac{\pi}{6}[/tex] et [tex] \alpha'=\frac{\pi}{3}[/tex]
J'ai alors [tex]x=R\frac{\sin{-\frac{\pi}{6}}}{\sin{\frac{\pi}{6}}}=-R[/tex]. ça colle...
Autres essais à venir...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#6 25-08-2016 16:42:11
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Re,
Avec [tex]\alpha=\frac{\pi}{6}[/tex] et [tex] \alpha'=\frac{\pi}{4}[/tex]
[tex]x=-0,57R[/tex] vraisemblable sur le dessin
Avec [tex]\alpha=\frac{\pi}{4}[/tex] et [tex] \alpha'=\frac{\pi}{3}[/tex]
[tex]x=-0,366R[/tex] vraisemblable sur le dessin
Avec [tex]\alpha=\frac{3\pi}{8}[/tex] et [tex] \alpha'=\frac{\pi}{4}[/tex]
[tex]x=0.412R[/tex] vraisemblable sur le dessin
Avec [tex]\alpha=\frac{pi}{3}[/tex] et [tex] \alpha'=\frac{\pi}{2}[/tex]
[tex]x=-0.58R[/tex] vraisemblable sur le dessin
Avec [tex]\alpha=\frac{\pi}{6}[/tex] et [tex] \alpha'=\frac{3\pi}{8}[/tex]
[tex]x=0.66R[/tex] vraisemblable sur le dessin
Avec [tex]\alpha=\frac{\pi}{6}[/tex] et [tex] \alpha'=\frac{3\pi}{8}[/tex]
[tex]x=-1,2R[/tex] P sort de [OB] confirmé sur le dessin....
Ce qui précède n'est pas une preuve; mais quel que soit [tex]\alpha[/tex] tel que [tex]0< \alpha\leqslant \frac{pi}{2}[/tex], que [tex]\alpha'[/tex] soit supérieur ou inférieur, les résultats obtenus ci-dessus sont cohérents avec le dessin...
@+
[EDIT]
Pour la formule d=f(x) j'en ai une mais que j'aimerais améliorer...
Voyons déjà si notre ami revient...
Dernière modification par yoshi (26-08-2016 11:53:19)
Arx Tarpeia Capitoli proxima...
Hors ligne
#7 30-08-2016 09:50:58
- KypKool
- Invité
Re : Cercle, triangle et fonctions
Bonjour,
Désolé je pensais recevoir des mail d'alerte lorsque tu répondais :p je viens de voir tes démonstrations
Très jolie utilisation de la colinéarité des deux vecteurs pour lier les inconnues, j'aime beaucoup :)
x est bien fonction de R et de l'élévation du point de départ ce qui semble bien logique.
Pour d = f(X), on a d = R(cosα′-cosα)
Tu es arrivé à isoler α′ comme étant une fonction de α et x ?
Je vais regarder ça en utilisant la colinearite :)
#8 30-08-2016 11:22:34
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Salut,
J'ai une formule liant x et d, mais c'est [tex]d=f(x,R,\alpha,\alpha')[/tex]
Or, x étant lui-même une fonction de [tex](R,\alpha,\alpha')[/tex], je n'en vois pas trop l'utilité...
Quant à isoler [tex]\alpha'[/tex] en fonction de d, R et [tex]\alpha[/tex], je n'y ai pas pensé : ça risque d'être coton.
Je regarderai.
Désolé je pensais recevoir des mail d'alerte lorsque tu répondais :p je viens de voir tes démonstrations
Si, si, c'est possible pour les membres, mais pas activé par défaut...
Je te préviens directement.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 30-08-2016 13:38:21
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Ave,
[tex]x=R\,\frac{\sin(\alpha-\alpha')}{\sin\alpha}[/tex] avec [tex]\alpha\in ]-\pi\;;\;0[[/tex]
[tex]\Leftrightarrow[/tex]
[tex]sin(\alpha-\alpha')=\frac{x\sin \alpha}{R}[/tex]
[tex]\Leftrightarrow[/tex]
[tex]\alpha-\alpha'=\arcsin\left(\frac{x\sin \alpha}{R}\right)[/tex]
[tex]\Leftrightarrow[/tex]
[tex]\alpha'=\alpha-\arcsin\left(\frac{x\sin \alpha}{R}\right)[/tex]
Mais c'est toujours la même problématique x est lui même fonction de [tex]R,\alpha,\alpha'[/tex]
Sauf si on fixe x et [tex]\alpha[/tex], par exemple
x=-0.5 et [tex]\alpha =\frac{\pi}{6}[/tex] et je prends R = 1 pour contrôler en proportion sur mon dessin geolabo où je fixe [tex]\alpha[/tex] et [tex]x[/tex] :
[tex]\alpha'=0.7762790307403775\;rad --> 0.7762790307403775*180/pi = 44.47751218592992^{\circ}[/tex]
Cohérent.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#10 01-09-2016 12:09:22
- KypKool
- Invité
Re : Cercle, triangle et fonctions
Salut,
Merci beaucoup pour ton aide.
Je vais pouvoir avancer avec la dernière formule de que tu as écrite. C'est ce dont j'avais besoin :)
Bien jouer encore pour avoir utiliser le critère de colinéarité entre les vecteurs, je m'enfermais dans les formules de trigonométrie pour essayer de trouver un pont entre avec mes inconnues.
J'espère que tu auras trouver le problème interessant ^^
#11 04-09-2016 21:12:35
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Re : Cercle, triangle et fonctions
Salut,
C'était surprenant, puis intéressant.
J'ai cherché simple, efficace et qui ne dépende pas d'un cas de figure : d'où l'emploi des vecteurs...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1
Discussion fermée








