Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 24-05-2017 23:00:34
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Etude des fonctions polynomes
Bonjour ici!
j'aimerai qu'on s'entraide un peu sur quelque exercice,sur la fonction.
voici le sujet:Etudiez les fonctions suivantes,en donnant chacunes leur ensemble de définition,et calculez leur dérivée si possible,et en déduire la courbe représentative.
A/F(x)=x^3 - 1
B/ F(x)=x
Hors ligne
#2 25-05-2017 01:03:41
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Etude des fonctions polynomes
Bonsoir,
Notre conception de l'entraide est d'essayer de débloquer les points qui posent problème.
Je cite le règlement du forum, que je t'invite à lire :
*Notre but étant de vous aider à résoudre vos difficultés, et non de faire les exercices à votre place, ne postez pas le sujet d'un exercice sans montrer que vous y avez travaillé : il n'y serait probablement pas répondu. A vous d'expliquer ce que vous avez déjà fait, là où vous bloquez, et pourquoi...
Qu'as-tu essayé de faire?
As-tu calculé les dérivée?
Où bloques-tu?
Pour répondre à ta question de l'autre discussion, l'ensemble de définition d'une fonction est l'ensemble des valeurs que la variable $x$ peut prendre.
Ici, ce sont des fonctions polynômes. Tu as dû avoir un cours là dessus. Quel est l'ensemble de définition d'un polynôme?
Dernière modification par tibo (25-05-2017 01:04:18)
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#3 25-05-2017 05:56:40
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Bonjour!
Ah,d'accord merci .
je regardais mes cours,une fonction polynome est définie dans |R.
Pour le calcul de la dérivée,je bloque un peu
Hors ligne
#4 25-05-2017 10:17:30
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Etude des fonctions polynomes
Bonjour,
En effet, les fonction polynômes sont définies sur $\mathbb{R}$.
À ton niveau, des valeurs interdites peuvent apparaître avec la fonction inverse (définie sur $\mathbb{R}^*$) et la fonction racine carrée (définie sur $\mathbb{R}+$).
Pour les dérivée je ne vois pas comment t'aider tant que tu n'as pas essayé quelque chose.
Ce sont des polynômes, les fonctions les plus simples à dériver. Tu en as forcément quelques exemples dans ton cours.
Et si tu ne sais pas dériver la $(B)$, c'est que tu n'as pas lu ton cours...
Au fait, tu es en quelle classe?
Dernière modification par tibo (25-05-2017 10:18:01)
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#5 25-05-2017 23:15:00
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Bonsoir.
je suis juste débutente,en mathématiques,je n'ai pas fait ça,dans ma vie mais je veux préparer un examen.,de maths pour un boulot
Hors ligne
#6 27-05-2017 19:31:06
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Etude des fonctions polynomes
Bonsoir,
Je m'excuse mais je n'ai pas le temps de refaire un cours complet sur les dérivées.
Il y a des cours très bien fait sur internet.
Je te propose celui-là, mais il en existe d'autres.
Si tu as des questions ponctuelles, je veux bien y répondre mais pas tout t'expliquer de A à Z.
Je me rend bien compte que ce message peut s'interpréter par "Débrouille toi toute seule.", mais ce n'est pas du tout ça.
Je ne me sens pas de refaire un cours.
Dernière modification par tibo (27-05-2017 19:31:41)
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#7 27-05-2017 21:14:27
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Bonsoir,
tibo a raison : un cours sur les dérivées bien fait prendrait de nombreuses pages...
Demain, je veux bien essayer de te faire un résumé de cours, en passant un certain nombre de choses : je me limiterai aux fonctions polynômes...
J'établirai les formules de base. Ensuite :
1. Il te faudra faire l'effort d'approfondir le cours,
2. Tu devras apprendre les formules et savoir les appliquer...
Pourquoi ne pas balancer les formules tout de suite alors ?
La réponse tient dans cette citation de Rabelais que j'aime à citer :
<< Science sans conscience n'est que ruine de l'âme. >>
Patiente jusqu'à demain matin...
Le soir, j'évite : trop de risques de mauvais choix de mots, d'exemples voire de fautes d'inattention...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 27-05-2017 21:29:39
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Bonsoirs à tous!
ok merci beaucoup pour votre aide les gars.
bonne soirée.
Hors ligne
#9 28-05-2017 10:47:56
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Bonjour,
Bon allons-y, je compte sur tibo pour annoter, parce que ce que je vais faire s'apparente à de la vulgarisation : je ne sais pas même pas ce que tu sais faire en Algèbre !...
Puristes, ne grimpez pas au mur, SVP... ;-)
Alors, disons que la dérivée d'une fonction f définie sur un intervalle I, est la limite
de [tex]\frac{f(x+h)-f(x)}{h}[/tex] (où x est la variable et h un nombre aussi petit qu'on veut) lorsque h tend vers (= prend des valeurs de plus en plus proche de) 0.
La plus simple des fonctions est la fonction constante : $f(x)=a$ où a est une constante, c'est à dire possède une valeur fixée mais qui n'est pas donnée, et qui ne dépend pas de x :
(f1)=a, f(2)=a... La dérivée de f est notée f'...
Que vaut f'(x) ?
Appliquons la définition :
[tex]f(x+h)=a[/tex] ; [tex]f(x) = a[/tex] donc [tex]\frac{f(x+h)-f(x)}{h}= \frac{a-a)}{h}=0[/tex]
Donc avec[tex] f(x)=\text{constante}[/tex] on a $f'(x)=0$
Prenons maintenant la plus simple des fonctions linéaires : $f(x) = x$... Quelle est sa dérivée ?
[tex]\frac{f(x+h)-f(x)}{h}=\frac{x+h-x}{h}=\frac{h}{h}=1[/tex]
J'ai le droit de simplifier parce que h n'est pas nul, il ne fait que tendre vers 0...
Et la dérivée de $ax$ ?[tex]f(x)=ax[/tex]
Appliquons la définition :
[tex]\frac{f(x+h)-f(x)}{h}=\frac{a(x+h)-ax}{h}=\frac{ax+ah-ax}{h}=\frac{ah}{h}=a[/tex]
$f'(x)=a$
Dérivée d'une fonction affine ? a et b étant deux constantes quelle est donc la dérivée de ax+b ?
[tex]\frac{f(x+h)-f(x)}{h}=\frac{a(x+h)+b-(ax+b)}{h}=\frac{ax+ah+b-ax-b}{h}=\frac{ah}{h}=a[/tex]
En fait, tu peux constater, que si f est la somme de deux fonctions g et k : f(x)=g(x)+k(x)
[tex]\frac{f(x+h)-f(x)}{h}=\frac{g(x+h)+k(x+h)-(g(x)+k(x))}{h}=\frac{g(x+h)-g(x)}{h}+\frac{k(x+h)-k(x)}{h}[/tex]
Et quand h tend vers 0,
* la limite de [tex]\frac{g(x+h)-g(x)}{h}[/tex] est $g'(x)$,
* la limite de [tex]\frac{k(x+h)-k(x)}{h}[/tex] est $k'(x)$,
D'où
(g+k)'=g'+k'
Ne tirons pas de conclusions hâtives, passons à la fonction carré : [tex]f(x)=x^2[/tex]. f'(x)= ?
Appliquons la définition :
[tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^2-x^2}{h}=\frac{x^2+2xh+h^2-x^2}{h}=\frac{2xh+h^2}{h}=\frac{h(2x+h)}{h}=2x+h[/tex]
Et si on fait tendre h vers 0, [tex]\frac{f(x+h)-f(x)}{h}[/tex] tend donc vers $2x$.
Si [tex]f(x)=x^2[/tex] alors[tex] f'(x)=2x[/tex]
Introduisons une constante : [tex]f(x)=ax^2[/tex]
[tex]\frac{f(x+h)-f(x)}{h}=\frac{(ax+h)^2-ax^2}{h}=\frac{a^2x^2+2axh+h^2-ax^2}{h}=\frac{2axh+h^2}{h}=\frac{h(2ax+h)}{h}=2ax+h[/tex]
Et si on fait tendre h vers 0, [tex]\frac{f(x+h)-f(x)}{h}[/tex] tend donc vers $2ax$.
Je continue avec la fonction cube
[tex]f(x)=x^3[/tex]
[tex]f'(x)=\lim_{h \to 0} \frac{(x+h)^3-x^3}{h}[/tex]
[tex]\frac{(x+h)^3-x^3}{h}=\frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}=\frac{h(3x^2+3xh+h^2}{h}=3x^2+3xh+h^2[/tex]
Et si on fait tendre h vers 0, alors [tex]3x^2+3xh+h^2[/tex] tend vers [tex]3x^2[/tex]
Donc formules :
[tex]f(x) = x^n\quad ;\quad f'(x)=nx^{n-1}[/tex]
On soustrait 1 à l'exposant et on multiplie par cet exposant.
Note bien que
a étant une constante si [tex]f(x)=ax^n[/tex] alors [tex]f'(x)=nax^{n-1}[/tex]
Si j'applique cette formule à
[tex]f(x)=ax[/tex], je note que[tex] f(x)=ax^1[/tex] : donc ici n =1
Donc [tex] (ax^1)'= 1ax^{1-1}=ax^0 = a[/tex]
Autre exemple [tex](ax^5-bx^2)' = ?[/tex] où a et b sont des constantes...
[tex](ax^5-bx^2)' = (ax^5)'-(bx^2)'=5ax^4-2bx[/tex]
N'oublie pas :
la dérivée d'une somme de fonctions s'obtient en faisant la somme des dérivées de chaque fonction.
Tu en sais assez pour faite tes exos et nous présenter les résultats...
Mais il te faudra aussi consulter un vrai cours...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#10 28-05-2017 12:12:44
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Etude des fonctions polynomes
Salut,
Mathématiquement, rien à redire.
Mais pour quelqu'un qui a peu l'habitude (je ne sais toujours pas si c'est le cas de Judithe), c'est relativement imbuvable. ^^
Surtout cette limite $\lim_{h\rightarrow 0}\dfrac{f(a+h)-f(a)}{h}$... (qui est quand même l'une des pires, et à enseigner sans avoir expliqué la notion de limite)
Pour l'introduire, j'aime bien l'approche graphique. Je te transmet le support que j'utilise : diapo
Il n'est pas parfait, et sans les explications que je donne à l'oral en parallèle, il perd un peu de substance mais bon.
Pour résumer, les propriétés à connaître sont les suivantes :
1) Soit $n$ un entier naturel.
Alors $(x\mapsto x^n)$ est dérivable sur $\mathbb{R}$ et sa dérivée est $(x\mapsto nx^{n-1})$
2) Soit $f$ et $g$ deux fonctions dérivables sur un intervalle $I$ et $\lambda$ un réel.
Alors
* $(f+g)$ est dérivable sur $I$ et sa dérivée est $(f'+g')$;
* $(\lambda f)$ est dérivable sur $I$ et sa dérivée est $(\lambda f')$.
Les démonstrations sont dans le post de yoshi.
Dans l'attente de te lire.
Dernière modification par tibo (28-05-2017 14:55:02)
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#11 28-05-2017 14:13:08
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Salut,
Bien d'accord...
Mais le problème est que si on commence à un peu trop formelliser, une chose en amenant une autre, on finit par ouvrir la boîte de Pandore...
Et là, on commence à s'approcher de trop près de l'ouverture de la boîte à questions...
En ce qui concerne donc le présent problème de Judithe, c'est que je pense que ce qu'elle sait, sur le plan théorique, tient "avec des bouts de ficelle"...
Tu vois mieux Judithe pourquoi tibo n'avait très envie de se lancer là-dedans ?
J'ai préféré rester dans l' "intuitif"...
J'ai donné dans le temps des cours de vulgarisation scientifique : c'était "sportif" !
Chercher la limite quand h tend vers 0 de [tex]\frac{f(x+h)-f(x)}{h}[/tex], c'est chercher en prenant, des valeurs de h successives de plus en plus proches de 0, vers quelle valeur ou expression finale vers quoi va arriver le quotient [tex]\frac{f(x+h)-f(x)}{h}[/tex], c'est cette expression finale qu'on appelle dérivée (avec[tex] f(x)=x^2[/tex]) :
h = 0,1 [tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+0,1)^2-x^2}{0,1}=\frac{0,2x+0,01}{0,1}=2x+0,1[/tex]
h=0,01 [tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+0,01)^2-x^2}{0,01}=\frac{0,02x+0,0001}{0,01}=2x+0,01[/tex]
h=0,001 [tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+0,001)^2-x^2}{0,001}=\frac{0,002x+0,000001}{0,001}=2x+0,001[/tex]
...............
h= 0,00001 [tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+0,00001)^2-x^2}{0,00001}=\frac{0,00002x+0,0000000001}{0,00001}=2x+0,00001[/tex]
Et là tu vois bien que la somme, lorsque le 2nd terme est suffisamment petit pour être considéré comme nul, se réduit à l'expression $2x$...
Ce que je viens de faire d'un pont de vue mathématique n'a pas valeur de preuve parce que ce ne sont que des exemples et qu'il faudrait les traiter sous sans exception : impossible...
C'est pourquoi, post #4, j'ai fait ça sans donner de valeur à h :
[tex]\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^2-x^2}{h}=\frac{x^2+2xh+h^2-x^2}{h}=\frac{2xh+h^2}{h}=\frac{h(2x+h)}{h}=2x+h[/tex]
Et si on fait tendre h vers 0, [tex]\frac{f(x+h)-f(x)}{h}[/tex] tend donc vers $2x$.
Traduire par :
Et si on donne à h des valeurs successives de plus en petites jusqu'à 0 $2x+h$ finit par s'écrire $2x$...
Quant à la dérivabilité, j'ai hésité puis j'ai opté pour l'omission : si je devine bien ce que Judithe aura à faire, demandera la technique...
Et, techniquement, je peux toujours calculer l'expression de la dérivée d'une fonction sans me préoccuper de sa dérivabilité...
Après, la notion de dérivabilité en un point donné, c'est une autre histoire, dont je persiste à penser que Judithe n'aura pas besoin...
Tiens, tibo, à ce propos, avais-tu lu cette discussion : http://www.bibmath.net/forums/viewtopic.php?id=5726 ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#12 28-05-2017 15:11:47
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Bonjour,
ok merci beaucoup,j'ai tout compris.
Hors ligne
#13 28-05-2017 15:28:02
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
mais j'ai une autre question,
comment faire pour être douée en algèbre?je veux être très douée en mathématiques.
Hors ligne
#14 28-05-2017 18:21:56
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Re,
Tout compris ? Parfait : et si tu nous donnais la solution de tes exercices...
Allez, on attend : c'est au pied du mur qu'on voit le maçon !
Être douée en Algèbre demande
1. De réduire le nombre de fautes de calcul au strict minimum (on n'est jamais à l'abri d'une étourderie), mais il faut, au cas où, être capable de la déceler et de la corriger, seul(e).
2. De maîtriser les diverses techniques à employer et savoir pourquoi on le fait et dans quelles conditions.
3. De faire un maximum d'exercices pour nourrir ton intuition : au bout de pas mal d'exercices, ton cerveau aura constitué une grosse "Banque de données", stockée dans ta mémoire à long terme... Ainsi, devant un exercice à la formulation jamais rencontrée, tu auras l' "intuition" du chemin à prendre pour le résoudre.
L'algèbre, c'est du raisonnement, au service duquel tu vas mettre tes capacités de calcul littéral (d'où le point n°1)...
Mais les mathématiques ne se réduisent pas à la seule algèbre !
@°
Arx Tarpeia Capitoli proxima...
Hors ligne
#15 28-05-2017 19:02:07
- tibo
- Membre expert
- Inscription : 23-01-2008
- Messages : 1 097
Re : Etude des fonctions polynomes
Re !
Il n'y a pas de secret. Pour devenir bon en mathématiques, il faut faire des tas et des tas d'exercices.
Toutes les pédagogies que l'on peut inventer ne sont là que pour essayer d'intéresser les élèves à la matière.
Mais au final, pour s'améliorer il n'y a pas d'autre solution que de passer par cette étape de rabâchage.
Mais je te rassure, cela ne signifie pas qu'il n'y a pas de plaisir à ça. À force on y prend goût et on en redemande !
@ yoshi (1) : Certes, je n'aurais pas dû parler de dérivabilité.
@ yoshi (2) : Non je n'avais pas lu cette discussion.
Vous vous êtes bien pris la tête quand même.
$x\sqrt{x}$ est définie sur $\mathbb{R}_+$ et dérivable sur $\mathbb{R}_+^*$ comme produit de fonctions dérivables sur $\mathbb{R}_+^*$.
Il reste donc la dérivabilité en 0 à étudier "à la main", ce qui est très rapide avec la limite du taux d'accroissement.
Fin !
A quoi sert une hyperbole?
----- A boire de l'hypersoupe pardi !
Hors ligne
#16 28-05-2017 22:32:01
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Rebonsoir.
vous voulez la solution de mon devoir.
A/F(x)= x^3 - 1
B/F(x)= x
Ce sont tous des fonctions polynomes,donc définie dans |R
Leur dérivé.Pour A,F'(x)= 3 x^2
Pour B,F'(x)= 1
Courbe représentative,B:y=x c'est l'équation d'une droite.
mais l'autre est une parabole
Hors ligne
#17 29-05-2017 10:35:36
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Bonjour,
Pour B oui, la courbe représentative des variations de f est bien une droite.
Je peux ajouter que
* cette droite passe par l'origine des coordonnées,
* c'est la première bissectrice des axes, la 2nde ayant pour équation [tex]y=-x[/tex]
* les droites d'équation y = x et y =-x sont perpendiculaires
Pour A, tu as répondu trop rapide
La courbe représentative de f telle que [tex] f(x)=x^3-1[/tex] n'est pas une parabole, c'est une courbe du 3e degré.
Maintenant dans le programme des révisions de ton examen, qu'est-ce qui est exigé à propos des fonctions ? Je présume, que cela ne se limite pas à savoir calculer une dérivée (dans ce cas, je n'en vois pas l'intérêt) mais aussi à l'étude complète d'une fonction ?
D'autre part, es-tu limitée au calculs des dérivées des seules fonctions polynômes ?
Voici une image avec deux courbes : en rouge celle qui correspond à ta question A, en bleu, une autre courbe du 3e degré...
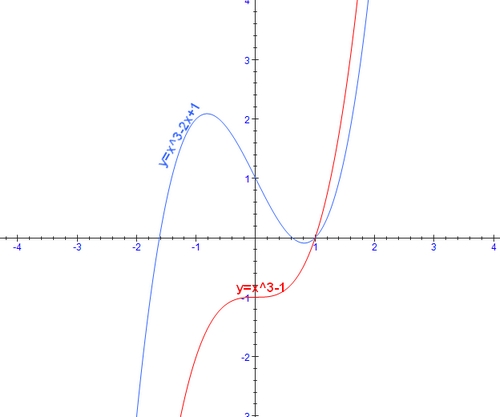
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#18 29-05-2017 15:14:14
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
rebonsoir!
ok merci beaucoup,Yoshi.
ben dans mes cours,on me demande une étude complète d'une fonction,que ce soit des polynomes,ou log.
Hors ligne
#19 29-05-2017 18:16:46
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
bonsoir,
C'est bien ce que je craignais...
Alors on continue...
Pour dériver [tex]f(x)=(2x-3)^2[/tex] par exemple, tu as trois options
1. Développer (et réduire si nécessaire) :
[tex]f(x)= 4x^2-12x+4[/tex] ce qui donne [tex]f'(x)=8x-12[/tex]
2. Ou faire appel à la notion de fonctions composées...
Ci-dessus, la fonction proposée est la composée des fonctions g et k telles que [tex]g(x)=2x-3[/tex] et [tex]h(x)=x^2[/tex] :
[tex] x \xrightarrow{g} 2x-3 \xrightarrow{h}(2x-3)^2[/tex]
Ici, on va poser U = 2x-3 et il faut chercher la dérivée de U^2...
Qu'est-ce que change l'écriture [tex]U^n[/tex] par rapport à [tex]x^n[/tex].
Dans la 2e forme, on se préoccupe pas de la dérivée de x puisque c'est 1, mais dans le 1er cas, si et on la note U'.
Si [tex](x^n)' = nx^{n-1}[/tex] celle de [tex]U^n[/tex] est [tex](U^n)'=nU'U^{n-1}[/tex]
[tex]U = 2x-3[/tex] donc [tex]U' = 2[/tex]
D'où [(2x-3)^2]' = 2\times 2\times (2x-3)= 8x-12
Autre exemple :
[tex][(x^2-3x+1)^3]' = \, ?[/tex] Là, la méthode n°1 est bien plus douloureuse...
Alors que
* on pose [tex]U =x^2-3x+1[/tex], on a donc [tex]U' = 2x-3[/tex]
* La formule nous donne [tex](U^3)' = 3U'U^2[/tex]
* d'où [tex][(x^2-3x+1)^3]' = 3\times (2x-3)(x^2-3x+1)^2[/tex]
Pigé ? Invente des exercices sur ce thème et donne-les nous à corriger
3. Je t'avais écris que la dérivée d'une somme, c'est la somme des dérivées [tex](U+V+W)'= U'+V'+W'[/tex]
Et je m'étais demandé si tu allais questionner au sujet de la dérivée d'un produit de fonctions, ou d'un quotient...
Bin non...
Mais vu ce que tu viens de dire au sujet de ton programme, je ne peux pas faire l'impasse dessus.
Je vais me contenter de te donner les formules !
[tex](U\times V)' =U'\times V+U \times V'[/tex]
Dans le cas de [tex] (2x-3)^2[/tex] je pouvais poser [tex]U = 2x-3[/tex] et [tex]V = 2x-3[/tex] D'où U' =2 et V' =2
[tex] [(2x-3)^2]'=[(2x-3)(2x-3)]' = 2(2x-3)+(2x-3)\times 2 = 4(2x-3)=8x-12[/tex]
Et le 2e exemple du point n°2, on pouvait aussi le faire comme ça ?
Oui, pas approprié mais faisable...
Par exemple,
[tex][(x^2-3x+1)^3]' =(x^2-3x+1)(x^2-3x+1)(x^2-3x+1)]'[/tex]
[tex]U = (x^2-3x+1)(x^2-3x+1)[/tex] d'où [tex]\quad U' = (2x-3)(x^2-3x+1)+(x^2-3x+1)(2x-3) =2(2x-3)(x^2-3x+1)[/tex]
[tex] V= x^2-3x+1[/tex] d'où [tex]V' = 2x-3[/tex]
On a donc :
[tex]U'V+UV'\,[/tex] :
[tex]2(2x-3)(x^2-3x+1)\times (x^2-3x+1) + (x^2-3x+1)^2\times (2x-3)[/tex]
[tex]=\; 2(2x-3)(x^2-3x+1)^2+(2x-3)(x^2-3x+1)^2= 3(2x-3)(x^2-3x+1)^2[/tex]
Tout pigé ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#20 29-05-2017 21:54:52
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Re,
Oui j'ai tout compris
Hors ligne
#21 30-05-2017 16:16:40
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Salut,
Alors, c'est bien...
Maintenant, je vais te montrer toutes les utilisations de la formule [tex](U^n)'=nU'U^{n-1}[/tex] : si on est assez malin elle remplace d'autres formules que, moi, lorsque j'étais Lycée, j'avais trouvé inutile de savoir...
Dans la forme donnée, il est dit nulle part que n doit être un entier naturel...
[tex]\left(\frac 1 x\right)'=-\frac{1}{x^2}[/tex] disent les formulaires...
[tex]\frac 1 x = x^{-1}[/tex]
D'où [tex](x^{-1})'=-1\times x^{-1-1}=-x^{-2}=-\frac{1}{x^2}[/tex]
Et :
[tex]\left(\frac{1}{x^2-3x+1}\right)'[/tex] ?
C'est [tex]U^{-1}[/tex] avec [tex]U = x^2-3x+1[/tex] et [tex]U' = 2x-3[/tex]
[tex](U^{-1})' =-U'U^{-2}[/tex] d'où
[tex]\left(\frac{1}{x^2-3x+1}\right)' = [(x^2-3x+1)^{-1}]'= -(2x-3)(x^2-3x+1)^{-2}=-\frac{2x-3}{(x^2-3x+1)^2}[/tex]
Et les racines carrées ?
Le cours dit : [tex] (\sqrt x)'=\frac{1}{2\sqrt x}[/tex]
Et moi je fais quoi ?
[tex](\sqrt x)' = \left(x^{\frac 1 2}\right)'=\frac 1 2x^{\frac 1 2-1}= \frac 1 2x^{-\frac 1 2} = \frac 1 2\times \frac{1}{\sqrt x}=\frac{1}{2\sqrt x}[/tex]
Parce que la racine carrée c'est la puissance 1/2, la racine cubique 1/3...
[tex]\left(\sqrt{x^2-3x+1}\right)'=\,?[/tex]
Je pose [tex]U = x^2-3x+1[/tex] et je cherche [tex](\sqrt U)'=\left(U^{\frac 1 2}\right)'[/tex]
[tex]\left(U^{\frac 1 2}\right)'=\frac 1 2U'U^{-\frac 1 2}[/tex]
Donc
[tex]\left(\sqrt{x^2-3x+1}\right)'=\frac 1 2(2x-3)(x^2-3x+1)^{-\frac 1 2}=\frac{2x-3}{2\sqrt{x^2-3x+1}}[/tex]
Maintenant, il reste encore le quotient de fonctions...
Le cours dit : [tex]=\frac{U'V-UV'}{V^2}[/tex]
Je peux retrouver cette formule en partant de [tex](UV)'=U'V+UV'[/tex] et en utilisant "l'astuce" du présent post...
En effet :
[tex]\frac U V =UV^{-1}[/tex]. La dérivée de $U$ c'est $U'$ mais celle de[tex] V^{-1}[/tex] est[tex] -V'V^{-2}[/tex]
D'où :
[tex]\left(UV^{-1}\right)'=U'V^{-1}+U(-V'V^{-2})=\frac{U'}{V}-\frac{UV'}{V^2}=\frac{U'V}{V^2}-\frac{UV'}{V^2}=\frac{U'V-UV'}{V^2}[/tex]
Tout va bien ?
Prochaine étape : étude du sens de variation d'une fonction en utilisant la dérivée...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#22 30-05-2017 21:40:47
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
Re,
oui j'ai tout lu et je comprends,je vais chercher des exos. et les traiter,appliquer les formules pour les retenir un peu.
merci d'avance.
L'étude du sens de variation d'une fonction dépend du dérivée(signe du dérivée)
puis les limites aux bornes de Df.
pour le notion des limites,je me bloque un peu.
Hors ligne
#23 31-05-2017 16:49:42
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Re,
T'a-t-on expliqué pourquoi le signe de la dérivée permet de connaître le sens de variation d'une fonction ?
En simplifiant et en restant imagé...
On va dire qu'une fonction possède 3 états : croissante, décroissante constante...
Prenons la courbe représentative d'une fonction f, et deux points distincts A et B sur cette courbe.
Le coordonnées de A et B sont [tex](x_A\,;\,f(x_A))[/tex] et [tex](x_B\,;\,f(x_B))[/tex].
Traçons la droite (AB) : on a une sécante de coefficient directeur [tex]m =\frac{f(x_B)-f(x_A)}{x_B-x_A}[/tex]
Sur cette courbe, dans le cas où c'est possible, déplaçons le point A de plus en plus proche vers le point B...
Que devient (AB) ? A terme, il n'y aura plus qu'une droite ; ce sera la tangente en B à la courbe...
Posons maintenant [tex]x_B-x_A ))=h[/tex]
le coefficient directeur de (AB) s'écrit :
[tex]m =\frac{f(x_A+h)-f(x_A)}{h}[/tex]
Ça doit te rappeler quelque chose...
Approcher A de plus en plus près de B, c'est faire tendre h vers 0...
Et m tend vers une limite :
[tex]\lim_{h\to 0} m =\lim_{h\to 0}\frac{f(x_A+h)-f(x_A)}{h}[/tex]
Et d'après ce qui est a été dit les jours précédents
[tex]\lim_{h\to 0}\frac{f(x_A+h)-f(x_A)}{h}[/tex] c'est la valeur de la dérivée de f au point B d'abscisse [tex]x_B[/tex]
Et m tend donc vers cette valeur de la dérivée de f au point B d'abscisse [tex]x_B[/tex], valeur qui ne sera autre que le coefficient directeur de tangente en B.
N-B : si [tex]m\to \pm\infty[/tex] cela signifie que la tangente en ce point est verticale...
si [tex]m\to 0[/tex] cela signifie que la tangente en ce point est horizontale : la fonction y admet un extremum, c'est à dire un minimum ou un maximum...
si m tend vers un nombre positif la fonction affine qui aura pour droite représentative ladite tangente sera croissante, et la fonction f aussi.
si m tend vers un nombre négatif la fonction affine qui aura pour droite représentative ladite tangente sera décroissante, et la fonction f aussi.
Donc à partir d'une fonction f quelconque, l'étude du signe de la dérivée te donnera le signe de la valeur de la dérivée en tout point du domaine de définition de f (et une étude de fonction, si le domaine n'est pas donné dans l'énoncé, commence par là), donc le signe du coefficient directeur de la tangente en tout point du domaine de définition de f, donc te permet de savoir si la fonction f est croissante ou décroissante sur un intervalle déterminé du domaine en question.
Pour le calcul des limites, ce n'est pas toujours simple, il arrive qu'on tombe sur une "indétermination" qu'il faut savoir lever ; et là, il y a du boulot : rien ne vaut l'accumulation des exercices... Eh oui...
Mais il faut connaître les cas d'indétermination :
[tex]\infty-\infty\,;\,0 \times\infty\,;\,\frac 0 0\,;\,\frac{\infty}{\infty}[/tex]
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#24 01-06-2017 12:29:57
- Judithe
- Membre
- Inscription : 24-05-2017
- Messages : 31
Re : Etude des fonctions polynomes
bonjour.
ok merci Yoshi.peut-on calculer l'équation de la tangente?et comment??
pourquoi le domaine de définition doit être donné bien au début?
Hors ligne
#25 01-06-2017 13:46:21
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Etude des fonctions polynomes
Salut,
pourquoi le domaine de définition doit être donné bien au début?
Pour ne pas faire d'opérations "illégales" par exemple calculer l'équation en un point dont l'abscisse n'appartient pas au domaine de définition...
Parce que tu connaîtras les intervalles où chercher le signe de la dérivée a un sens...
ok merci Yoshi.peut-on calculer l'équation de la tangente?et comment??
Alloons, allons ne me dis que si tu connais les coordonnées d'un point d'une courbe et le coefficient directeur de la tangente en ce point, tu ne sais pas calculer l'équation de cette tangente...
C'est quand même le B-A-BA de la géométrie analytique...
Oublie provisoirement le mot tangente...
Tu as une courbe, un point - dont tu connais les coordonnées -sur la courbe et tu as le coefficient directeur d'une des droites passant par ce point : calculer l'équation de cette droite c'est résoudre l'équation y = mx+p où x et y sont les coordonnées du point et m le coefficient directeur.
J'ai dit "une droite"...
Si tu changes de coefficient directeur, tu n'as plus la même droite (passant par un point donné, on peut trouver une infinité de droites) et si comme coefficient directeur, tu prends celui de la tangente, alors l'équation trouvée sera celle de la tangente...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne








