Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
#1 23-03-2017 00:34:37
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Géométrie
Bonsoir,
Me voilà avec un nouveau chapitre. Je commence la lecture de cette nouvelle leçon: Droite, segment, cercle, perpendicularité, parallélisme.
Ma première question: Pourquoi me dit on qu'il y a une différence entre un segment [AB] et la longueur AB de ce segment ?
2) Comment peut on dire que deux segments ont la même longueur mais ne sont pas égaux ?
Je vous remercie.
Hors ligne
#2 23-03-2017 09:05:59
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Bonjour,
Rien d'affolant là-dedans : juste préciser les notions.
Points, Segments, Droites, Demi-droites sont des objets géométriques...
Dore que deux objets géométriques sont égaux c'est dire que c'est le même objet : il n'y a en fait qu'un seul objet.
Si je dessine dans le plan 3 segments distincts avec n'importe quelle orientation [AB], [CD], [EF] et que ces segments sont superposables, alors on dira qu'ils ont une propriété caractéristique commune qu'on appellera longueur...
Les longueurs se mesurent.
Pour trouver la mesure de la longueur commune AB, CD ou EF de mes segments ci-dessus je dois choisir un segment de base comme unité de mesure des longueurs.
Par définition donc, on dira que la mesure longueur de ce 4e segment est 1.
Attention aux notations :
segment : utiliser des crochets --> [AB]. [AB] ou [BA] c'est le même segment
droite : utiliser des parenthèses --> (AB). (AB) ou (BA) c'est la même droite : elle passe par les points A et B....
demi-droite : utiliser crochet et parenthèse --> [AB) ou [BA) mais il y a là deux demi-droites distinctes.
[AB) a pour origine A et passe par B, [BA) a pour origine B et passe par A.
longueurs : ni crochets, ni parenthèses : AB, CD, EF...
Concrètement.
Dans le système métrique, l'unité légale des longueurs est le mètre. Toutes les longueurs sont mesurées par comparaison avec le mètre...
Comme ce n'est idéal on a créé des unités multiples du mètre : dam, hm, km et sous-multiples mm, cm, dm notamment...
Il y a longtemps eu (et doit y avoir encore) déposé au pavillon des Poids et Mesures à Sèvres un mètre-étalon en platine irridié qui était la référence en France de l'unité de longueur le mètre.
Si tu changes d'unité de longueur, tu changes la mesure de la longueur, pas la longueur elle-même.
Je ne veux pas aller plus loin pour ne pas t'embrouiller et que je ne sais pas non plus ce que raconte ton cours...
Tu auras sûrement beaucoup de questions; rien de plus normal, on y répondra au fur et à mesure...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#3 24-03-2017 01:46:09
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Re : Géométrie
Bonsoir,
Je vous remercie pour ces précisions.
Fini de lire la première partie et pour l'instant pas de questions (en même temps je n'ai pas fait les exos, ça, ça sera au moment de mes entraînements début avril), j'attaque demain les angles et polygones....
Hors ligne
#4 28-03-2017 22:51:40
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Re : Géométrie
Bonsoir,
Je n'ai pas rencontré de pbs particulier ces derniers jours mais là avec Thalès et la trigonmétrie me cause quelques tracas.
Voici mes "quelques" questions:
1) A propos de cette forme: http://www.cjoint.com/c/GCCuwecAO4U
Il faut que je trouve la mesure de OS
Les droites (PQ) et (RS) sont parallèles, avec les sécantes (QR) et (PS); d'après le théorème de Thalès on a: [tex]\frac{OR}{OQ}[/tex] = [tex]\frac{OS}{OP}[/tex]
donc [tex]\frac{5}{4}[/tex] = [tex]\frac{OS}{3}[/tex] donc OS= 15/4
Pourquoi je ne saisis pas ce résultat ?
2) Ma question concerne cette figure http://www.cjoint.com/c/GCCuGIuhHaU
Voilà on me dit que je dois utiliser le théorème de Thalès pour savoir si telle droite et telle droite sont parallèles. Or, là, avec cette configuration là on me dit que je ne peux pas "utiliser" le théorème dans sa totalité car les rapports [tex]\frac{MN}{BC}[/tex] ne sont pas égaux. Pourquoi ? Je ne vois pas la différence avec par exemple [tex]\frac{AM}{AB}[/tex] ...
3) Alors là, je me suis tirée les cheveux, encore une fois avec théorème de Thalès qui permet de partager un segment en segments égaux. Je n'arrive pas à reproduire la procédure.
Exemple: Partager le segment [AB] en 5 segments de longueurs égales avec un compas et une règle non graduée. On trace une demi droite [Ax). On reporte avec le compas, sur cette demi droite, à partir de A cinq segments consécutifs d'une même longueur arbitrairement choisie. Soit C le dernier point obtenu. On trace la droite (BC), puis les parallèles à (BC) qui passent par les point obtenus avec le compas.
On me demande de faire la même chose sur un autre segment et de le diviser en 7. Comment je fais ? Au pif ? je ne comprends pas, on m'impose un nombre et je ne parviens pas sans mesure à le faire sur un segment déjà défini. J'ai tracé ma demi droite mais rien ne correspond...
4) Trigonométrie
Si ABC est un triangle rectangle en C, alors [tex]cos^2[/tex]Â + [tex]sin^2[/tex]Â = 1
Avec AC = 3
CB=7
AB=10
beh je ne trouve pas 1 ... mais pour 7, je trouve 0.49 et pour 0.09, ça ne fait pas 1 (ne vous tirez pas les cheveux)
Ou peut être, qu'il faut utiliser une touche spéciale sur une calculatrice adaptée (que je ne me suis pas encore procurée)...
5) Je me mélange les pinceaux, j'ai l'impression qu'on agit de la même manière avec SOH CAH TOA pour calculer un angle ou une longueur ?
Je vous remercie....
Dernière modification par sarah2811 (28-03-2017 22:52:28)
Hors ligne
#5 29-03-2017 13:56:51
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Bonjour,
Point 1
Utiliser le théorème de Thalès dans le triangle pour calculer la longueur d'un côté, c'est se servir de la proportionnalité.
Je transforme ton égalité en tableau de proportionnalité :
5 | ?
--- |--- aurais-tu oublié les produits en croix ?
4 | 3
Autres méthodes :
[tex]\frac 5 4 = \frac x 3[/tex]
Je multiplie les deux membres par 3 : [tex]3\times \frac 5 4 =3 \times \frac x 3[/tex]
Ce qui donne [tex]\frac {15}{4}=x[/tex]
[tex]\frac 5 4 = \frac x 3[/tex] tu as une égalité de rapports de fractions, les produits en croix sont donc égaux [tex]4\times x = 5\times 3[/tex]
Soit [tex]4x = 15[/tex] et encore [tex]x = \frac{15}{4}[/tex]
Point 2.
Voilà on me dit que je dois utiliser le théorème de Thalès pour savoir si telle droite et telle droite sont parallèles.
Cette formulation est ambigüe et douteuse, je te renvoie à cette page : http://www.bibmath.net/ressources/colle … Thales.pdf
Puis tu écris :
là on me dit que je ne peux pas "utiliser" le théorème dans sa totalité car les rapports [tex]\frac{MN}{BC}[/tex] ne sont pas égaux.
les rapports : les ? voilà un pluriel bien... singulier : Je ne vois qu'un seul rapport...
on ne peut pas "utiliser" le théorème dans sa totalité : cette formulation est fidèle ç ce qu'on t'a écrit dans le cours ?
Si oui, c'est gênant : c'est du charabia...
En Logique (partie des mathématiques), on distingue
* le théorème de Machin : si propriété A vraie alors alors propriété B
* la réciproque du théorème de Machin : si propriété B vraie alors alors propriété A
* la contraposée du théorème de Machin : si propriété B fausse alors alors propriété A fausse (en Collège, on ne prononce pas ce terme de contraposée)
Si à la place de Machin j'écris Thalès, j'ai :
* droites parallèles (qui coupent des sécantes) ==> rapports égaux (théorème de T)
* rapports égaux + points placés dans le même ordre sur des sécantes ==> droites // (réciproque du théorème de T)
* rapports non égaux + points placés dans le même ordre sur des sécantes ==> droites non // (contraposée du théorème de T)
Je peux adapter ce qui est écrit ci-dessus en mettant aussi Pythagore à la place de Machin.
J'espère que tu as réponse à tes questions quand même parce que sans autre précision (mesures des longueurs ?) impossible de répondre clairement.
Point n°3
3) Alors là, je me suis tirée les cheveux, encore une fois avec théorème de Thalès qui permet de partager un segment en segments égaux. Je n'arrive pas à reproduire la procédure.
Exemple: Partager le segment [AB] en 5 segments de longueurs égales avec un compas et une règle non graduée. On trace une demi droite [Ax). On reporte avec le compas, sur cette demi droite, à partir de A cinq segments consécutifs d'une même longueur arbitrairement choisie. Soit C le dernier point obtenu. On trace la droite (BC), puis les parallèles à (BC) qui passent par les point obtenus avec le compas.On me demande de faire la même chose sur un autre segment et de le diviser en 7. Comment je fais ? Au pif ? je ne comprends pas, on m'impose un nombre et je ne parviens pas sans mesure à le faire sur un segment déjà défini. J'ai tracé ma demi droite mais rien ne correspond...
Tsss ! tsss ! Tu vas finir par devoir budgéter l'achat d'une perruque... ^_^
* Tu traces un segment [AB] d'une longueur quelconque
* Tu traces une demi-droite [tex][Ax[/tex] quelconque mais telle que B n'est pas sur cette demi-droite.
* Tu choisis une ouverture de compas quelconque pas trop petite ni trop grande.
* Puis, sur cette demi_droite, tu reportes successivement ton ouverture (en partant de A), pour obtenir les points C, D, E, F, G, H, I :
AC = CD = DE = EF = FG = GH = HI
* Tu traces alors la droite (IB).
* Puis les parallèles à (BI), passant par H, G, F, E, D, C. Tracer la parallèle à (IB) passant par H revient à tracer avec un compas un angle [tex]\hat H[/tex] tel que [tex]\hat H=\widehat{AIB}[/tex]. Si c'est ça qui coince, je t'envoie une explication en image.
* Ces parallèles coupent [AB] en H', G', F', R', D', C'. Les parallèles (IB), (HH'), (GG'), (FF'), (EE'), (DD'), (CC') sont appelées parallèles équidistantes. Et des parallèles équidistantes découpent un segment en longueurs égales AC' = C'D' = D'E' = E'F' =F'G' = G'H' = H'B
Point n°4
Si tu ne travailles pas dans un triangle rectangle ça ne marche pas, bien sûr...
Regarde
* [tex]AB^2 = 100[/tex] et [tex]BC^2+AC^2 = 49 + 9 = 58[/tex] et comme tu as [tex]AB^2 \neq BC^2+AC^2[/tex], alors le triangle n'est pas rectangle (contraposée du théorème du théorème de Pythagore).
* En prime [tex]AB = 10 = 3 + 7 = AC + CB[/tex] et j'en déduis que que les points A, C et B sont alignés dans cet ordre et qu'il n'y a pas de triangle non plus.
Recommence donc avec AB = 5, AC =3 et BC = 4 : c'est le plus petit triangle rectangle à côtés entiers. On peut en déduire toute une famille en multipliant chaque longueur par un nombre quelconque (non nul !)
Itou avec AB = 13, AC =5 et BC = 12 (mais là, pour travailler proprement, il te faudrait garder les fractions)
Point 5
Je t'envoie un résumé en 1 page seule : ça devrait t'aider...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#6 30-03-2017 00:07:36
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Re : Géométrie
Bonsoir,
Point 1
Utiliser le théorème de Thalès dans le triangle pour calculer la longueur d'un côté, c'est se servir de la proportionnalité.
Je transforme ton égalité en tableau de proportionnalité : aurais-tu oublié les produits en croix ?
Mais bien sûr !! Vous me croyez si je vous dit que j'y ai pensé plus d'une fois ?? En fait, je n'arrivais pas à comprendre pourquoi on me proposait un [tex]\frac{15}{4}[/tex], alors que je me disais que le résultat était 3,75.
Concernant le Point 2.
Merci pour le lien, j'imprime demain et je lirai cela.
Toutefois, j'ai regardé rapidement, et je me rends compte que dans mon ouvrage, on me propose les deux mêmes configurations que vous me proposez. Or, dans mon ouvrage (et c'était ma remarque que j'ai mal exprimée avec une alternance de singulier et de pluriel), on me dit pour la première configuration (celle qui est placée au dessus dans votre document), mot pour mot: " Dans les conditions de la configuration 1, on a également [tex]\frac{AM}{MB}=\frac{AN}{NC}[/tex] mais, attention, ces rapports ne sont pas égaux à [tex]\frac{MN}{BC}[/tex]." Là c'est moi qui parle, et en vous posant la question, je me demande si ça me servira à quelque chose de savoir pourquoi ... (même si j'imagine que vous me direz qu'il faut toujours savoir pourquoi..., donc je me lance) Pourquoi ce rapport ne sera pas égal aux autres dans la première configuration alors qu'il le sera dans la deuxième ?
Toutefois, si vous pensez partir dans des explications qui soient trop ardues, n'hésitez pas à sauter ce point...
Point 3.
* Puis les parallèles à (BI), passant par H, G, F, E, D, C. Tracer la parallèle à (IB) passant par H revient à tracer avec un compas un angle H^H^ tel que H^=AIBˆH^=AIB^ . Si c'est ça qui coince, je t'envoie une explication en image.
Je crois que je vais être obligée de vous demander une explication en image :-(
En effet pas de problème pour la première partie où je dois placer mes points sur la demie droite, mais quand il s'agit de placer les points sur le segment [AB], je ne vois pas comment faire, ça coince...avec un compas et une règle non graduée, je ne vois pas....
Point 4:
Bien sûr, où avais je la tête, je me suis lancée des mesures au hasard, oubliant que le théorème fonctionnait avec les triangles rectangles. Je vous remercie...
Point 5: Merci, je vais aller voir ça...
Deux autres nouvelles questions pour fêter la fin de ma "lecture", (il était temps à 20 jours des épreuves)
Dans le chapitre Transformations:Centre de symétrie
On me propose un rectangle, un triangle, losange, carré...
On identifie pour chacun d'entre eux un certain nombre d'axes et de centres de symétries.
Ma question: Comment peut il y avoir un centre de symétrie sans axe existant comme pour le parallélogramme ? Et comment peut il y a voir des axes sans centre de symétrie comme pour le triangle équilatéral ?
Autre Question, concernant la rotation.
Là je ne comprends rien, peut être à cause des signes ... J'ai compris le principe de la rotation, c'est la définition que j'ai du mal à comprendre.
Voici la définition mathématique (parce que l'on me propose juste avant une définition naïve):
Etant donné un angle avec un 0 et une barre au milieu - (que veut dire ce signe) (de sens direct ou indirect) et un point C, l'image du point M par la rotation de centre C et d'angle avec un 0 et une barre au milieu - est:
-le point M' tel que CM'=CM et l'angle (CM'CM) avec un chapeau au dessus de tout ça = 0 avec la barre au milieu (de sens direct ou indirect), si M est diférent de C
-le point lui même si M est en C
La rotation de centre C et d'angle 0 avec la barre au milieu est notée R (C, 0 avec la barre au milieu)
Est ce que ce 0 avec la barre au milieu, renvoie à une sorte de [tex]x[/tex] dans les équations ?
Je vous remercie....
PS: le forum est réglé à l'heure d'hiver encore, non ? parce que là il est 00:52 et je vois que la dernière modif de mon post est affichée à 23h52.
Dernière modification par sarah2811 (30-03-2017 00:53:58)
Hors ligne
#7 30-03-2017 14:19:15
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Bonjour,
Point 2.
Je te dois des excuses.
J'ai mal regardé le dessin. En fait, je faisais des aller-et-retour entre ton texte, tes dessins et ce que j'avais presque fini d'écrire. Et puis, j'ai gaffé, j'ai fermé BibMath... et j'ai dû tout recommencer ! En prime, ce matin, j'ai eu une panne d'Internet de 2 h sans raison qui m'a obligé à m'interrompre
Les rapports du théorème de Thalès sont exclusivement (pour une bonne raison) :
[tex]\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}[/tex]
Le 3e rapport est parfois qualifié de rapport complémentaire...
En fait, c'est une habitude que de les écrire dans ce sens. Pour les besoins de ma démonstration, je vais inverser les rapports, ce sera plus facile à voir.
Donc on peut écrire aussi :
[tex]\frac{AB}{AM}=\frac{AC}{AN}=\frac{BC}{MN}[/tex]
J'en extrais ces deux-ci :
Etant donné que M est entre A et B, je peux écrire AB = AM + MB
Je remplace AB dans l'égalité ci-dessus :
[tex]\frac{AM+MB}{AM}=\frac{BC}{MN}[/tex]
Je décompose la première fraction en une somme de deux fractions de même dénominateur :
[tex]\frac{AM}{AM}+\frac{MB}{AM}=\frac{BC}{MN}[/tex]
Je simplifie la première fraction :
[tex]1+\frac{MB}{AM}=\frac{BC}{MN}[/tex]
Donc tu vois que
[tex]\frac{MB}{AM}\neq\frac{BC}{MN}[/tex]
Si je suis la même procédure avec l'égalité [tex]\frac{AC}{AN}=\frac{BC}{MN}[/tex]
J'arrive à :
[tex]1+\frac{NC}{AN}=\frac{BC}{MN}[/tex]
Et donc :
[tex]\frac{NC}{AN}\neq\frac{BC}{MN}[/tex]
Pourtant en partant de :
[tex]\frac{AB}{AM}=\frac{AC}{AN}[/tex]
J'aboutis à :
[tex]1+\frac{MB}{AM}=1+\frac{NC}{AN}[/tex] et, en soustrayant 1 de chaque côté : [tex]\frac{MB}{AM}=\frac{NC}{AN}[/tex]
Et en inversant ;
[tex]\frac{AM}{MB}=\frac{AN}{NC}[/tex]
Ces conclusions obtenues sans calculs basés sur des valeurs numériques particulières, sont donc toujours vraies...
Ces calculs littéraux risquant de te paraître durs à digérer, je vais tenter une explication concrète.
On construit un triangle AMN quelconque...
Sur [AM), on place le point B tel que (par exemple) AB = 3 AM.
Sur [AN), on place le point C tel que AB = 3 AM.
Les points A, M, B d'une part et A, N, C étant placés dans le même ordre sur (AB) et (AC) et comme[tex] \frac{AM}{AB}=\frac{AN}{AC}=\frac 1 3[/tex], la réciproque du théorème de Thalès permet de dire qu'on a bien (MN)//(BC).
Maintenant que je sais que les droites (MN) et (BC) sont parallèles, je peux appliquer, cette fois, le théorème de Thalès !
Qui va me permettre d'ajouter que [tex]\frac{MN}{BC}=\frac 1 3[/tex] aussi.
Que vaut [tex]\frac{AM}{MB}[/tex] ?
Puisque AB = 3AM alors MB = 2 AM et donc [tex]\frac{AM}{MB}=\frac{AM}{2AM}=\frac 1 2[/tex] et non [tex]\frac 1 3[/tex]
Ça te va ?
En fait, je n'arrivais pas à comprendre pourquoi on me proposait un \frac{15}{4} , alors que je me disais que le résultat était 3,75.
Oui, mais tu ne l'as pas dit et moi, je n'ai pas pensé du tout à ça...
Un prof de Maths est un être bizarre qui ne jure que par les fractions : il n'utilise les nombres décimaux que par défaut... parce qu'une fraction quelle qu'elle soit est toujours une écriture du quotient exact du numérateur par le dénominateur ; dans la majorité des cas, c'est même la seule écriture du quotient exact...
Je crois que je vais être obligée de vous demander une explication en image :-(
Je vais m'y atteler et je te l'enverrai.
Ce n'est pas naturel de tracer des parallèles avec compas et règle non graduée. De le demander avec compas/règle non graduée rajoute un non-dit que je vais t'expliquer.
J'ignore si tu as vu une leçon traitant des angles et des droites parallèles (1ere page de mon dico).
A. B. C.
/ /
D/ E/
/ /
Les angles [tex]\widehat{ABD}[/tex] et [tex]\widehat{ACE}[/tex] occupent une position bien particulière : on dit qu'ils sont en position d'angles correspondants (qu'on abrège en : angles correspondants).
Si deux angles sont correspondants ET égaux alors les droites sont parallèles.
Donc dans ce que je t'ai expliqué, on démarre avec un angle [tex]\widehat{AIB}[/tex]
Et si tu traces alors un angle [tex]\widehat{AHx}[/tex] tel que [tex]\widehat{AHx}=\widehat{AIB}[/tex], ces deux angles sont correspondants et égaux. Alors on a [tex](Hx)//(IB)[/tex] et l'intersection de [tex](Hx)[/tex] avec ton segment [AB] te donne le point I' cherché.
Et tu recommences en partant de G...
le tout c'est de tracer un angle égal à un angle donné.
La méthode qu'on explique en 6e c'est commencer tracer une parallèle à une droite donnée en utilisant règle et équerre non graduées ! c'est déjà assez difficile à maîtriser pour beaucoup, mais ça leur paraît naturel lorsqu'ils font glisser l'équerre sur la règle que les droites sont parallèles. Les Dessinateurs Industriels lorsqu'ils traçaient les plans des pièces ne faisaient pas autre chose...
Et tu n'auras pas à enseigner (je dirais même : il ne faudra pas) une autre méthode à tes futurs élèves je pense.
Ma question: Comment peut il y avoir un centre de symétrie sans axe existant comme pour le parallélogramme ? Et comment peut il y a voir des axes sans centre de symétrie comme pour le triangle équilatéral ?
Hmmmm...
Je dirais :
la notion de centre de symétrie est liée à la notion de milieu
celle d'axe de symétrie est liée à la notion de médiatrice, donc de milieu et d'angle droit...
Le symétrique d'une droite par rapport à un point est toujours une droite parallèle.
Prenons deux droites parallèles quelconques ($\Delta$) et ($\Delta$') et un point A sur ($\Delta$) et B sur ($\Delta$').
J'appelle M le milieu de [AB] : Les deux droites sont toujours symétriques par rapport à M, peu importe les positions respectives de A et B l'un par rapport à l'autre...
Prenons encore un point C sur ($\Delta$). En traçant [CM), je coupe ($\Delta$') en D.
D'après la définition, D est le symétrique de C par rapport à M. Et le segment [CD] est le symétrique du segment [AB] par rapport à M.
[AB] et [CD] sont-ils symétriques par rapport à une droite ou à quelle condition le sont-ils ?
Supposons qu'il existe une droite telle que [CD] soit le symétrique de [AB], autrement dit que le quadrilatère ACBD ait un axe de symétrie.
Prenons le point A.
Quel pourrait être son symétrique ? Réponse (évidente) C, B ou D...
Si c'était C, alors cet axe symétrie serait la médiatrice de [AC]....
Pour quelle raison alors B et D seraient-ils symétriques ? Il faudrait que la médiatrice de [AC] soit aussi celle de [BD]... Et comme j'ai choisi arbitrairement les postions de A, B et C, il y a peu de chances que ce soit le cas, et même très peu de chances... Il faudrait que ACBD soit un rectangle... Or dans la majorité des cas, ce n'est qu'un simple parallélogramme...
Si c'était B, alors l'axe de symétrie serait la médiatrice de [AB].
Pourrait-elle être la médiatrice de [CD] ? Non, à cause de ma construction : les droites (AB) et 'CD) sont sécantes, et la médiatrice de [AB] ne peut être celle de [CD] que si (condition nécessaire mais pas suffisante) (AB) et (CD) sont parallèles ce qui n'est pas le cas.
Si c'était D, enfin ? On serait bien dans le cas ci-dessus ! Oui mais, dans ce cas la médiatrice de [AD] est aussi celle de [BC]..3. Ce qui n'est possible qu'à une condition supplémentaire. Soient R et S les milieux de [AD] et [BC]. Il est facile (pour moi) de montrer que (RS) // (AB) //(DC) et si (RS) est médiatrice de [AD] et [CB] alors les angles [tex]\hat R[/tex] sont droits. Ce qui entraine que ACSR et DBSR sont des rectangles et ACBD aussi.
Or, dans la très grande majorité des cas, les points A, C et B ayant été placés totalement arbitrairement sur ($\Delta$) et ($Delta$'), il y a très, très peu de chances que ACBD soit un rectangle...
Dans le cas du rectangle pour que chaque diagonale soit axe de symétrie, il faut que le rectangle possède en plus les propriétés du losange, donc soit un carré...
Est ce que ce 0 avec la barre au milieu, renvoie à une sorte de x dans les équations ?
[tex]\theta[/tex] donc ? Ce n'est que la lettre grecque theta qui est un nom habituel pour un angle, au même titre que souvent on parle d'un angle alpha [tex]\alpha[/tex]
Dans la rotation désignée par [tex]R(C,\theta)[/tex], l'image d'un point M est le point M' tel que CM = CM' et [tex]\widehat{MCM'}=\theta[/tex]
La rotation conserve les angles, les longueurs, les milieux.
Soit un triangle ABC quelconque, un point D en dehors (c'est plus simple à voir) de ABC, et un angle [tex]\theta[/tex] quelconque.
L'image de ABC dans la rotation [tex]R(D,\theta)[/tex] est un triangle A'B'C' parfaitement superposable à ABC. Si ABC était isocèle, équilatéral... A'B'C' le serait aussi.
Soit M le milieu de [AB], l'image de M dans cette rotation est le point M' milieu de [A'B'].
N-B Si [tex]\theta = 180^{\circ}[/tex] alors la rotation [tex]R(D,\theta)[/tex] revient à la symétrie centrale de centre D...
Translation : c'est un déplacement rectiligne sans déformation.
Les deux sont répertoriés dans mon dico.
J'attaque ton dessin. Je vais remplacer le dessin du compas par un segment fléché comme celui-ci : [tex]\longleftrightarrow[/tex].
Je te l'envoie dès qu'il est fini.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 30-03-2017 19:43:34
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Re,
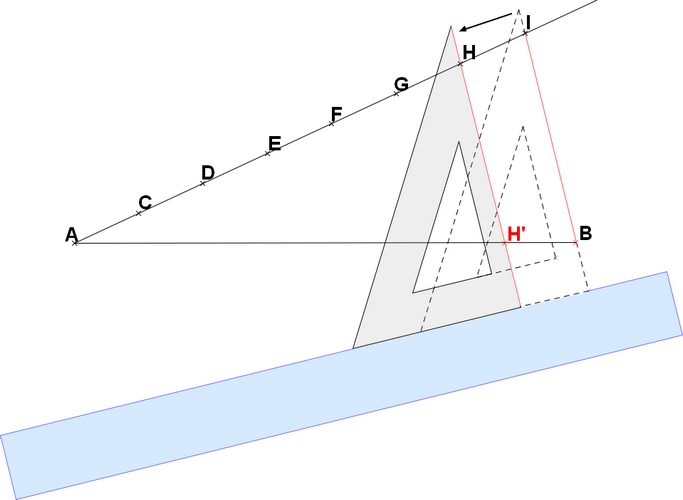
Je vais légèrement modifier la procédure et la standardiser (je serais curieux de voir comment ils ont fait) : ce n'est pas aussi évident que je le pensais : je ne dois pas employer la même méthode, mais jusqu'à preuve du contraire (pose l'image de la méthode à 5 sur cjoint quand même). Ce que je propose limite le nombre de tracés.
Je change d'avis, pas d'envoi : dessin ci-dessous.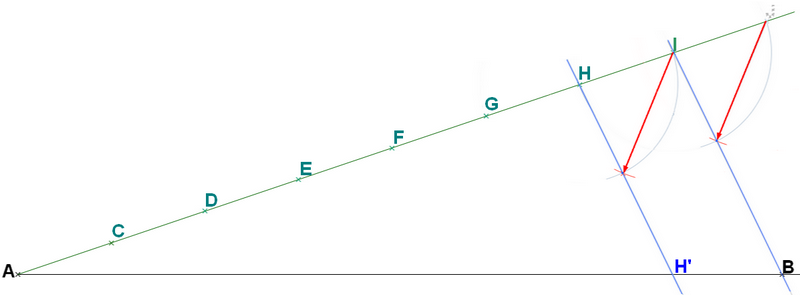
L'ouverture de compas sera désignée par [tex]\longrightarrow[/tex] et non plus [tex]\longleftrightarrow[/tex] : la pointe de flèche est la mine et l'autre bout, la pointe sèche du compas ((quand même, de tête - à l'aveugle comme on dit aux Echecs -, je ne pensais pas avoir besoin d'un 8e point. Ça me chiffonne...)
1. Tu places un 8e point J (que j'ai pointillé) sur [AI) tel que [tex]\cdots = HI = IJ[/tex]. Je compte pas A dans les 8 (sinon 9e).
2. Tu traces un arc de cercle de centre I et de rayon [IJ] : il va recouper [IB) en un point à qui je donne le nom générique de Z.
3. Tu traces un arc de cercle de centre H et de rayon [HI]
4. La pointe sur J, tu ouvres le compas de façon à ce que la mine se place en Z : ce sera la longueur de la corde commune matérialisée en rouge --->
5. Ceci fait, tu lèves le compas, garde la même ouverture, tu places ta pointe en I, et tu traces l'arc de cercle de centre I qui aura comme rayon ton ouverture de compas.
6. L'intersection Z1 des deux arcs de cercle est le deuxième point de la droite parallèle : trace aloirs [HZ1) qui va couper [AB] en H'.
Maintenant on recommence à partir du 3. et du point G.
3. Tu traces un arc de cercle de centre G et de rayon [GH]
4. La pointe sur J, tu ouvres le compas de façon à ce que la mine se place en Z : ce sera la longueur de la corde commune matérialisée en rouge --->
5. Ceci fait, tu lèves le compas, garde la même ouverture, tu places ta pointe en I, et tu traces l'arc de cercle de centre I qui aura comme rayon ton ouverture de compas.
6. L'intersection Z2 des deux arcs de cercle est le deuxième point de la droite parallèle : trace aloirs [GZ2) qui va couper [AB] en G'.
Et ainsi de suite jusqu'à C. Ce que j'ai fait est conforme au document envoyé qui donne la méthode de reproduction d'un angle à la règle et au compas...
Mais je viens de trouver plus rapide et plus simple sans copier un angle.
Je vais construire des losanges en utilisant la propriété : si un quadrilatère a ses 4 côtés de même longueur alors c'est un losange.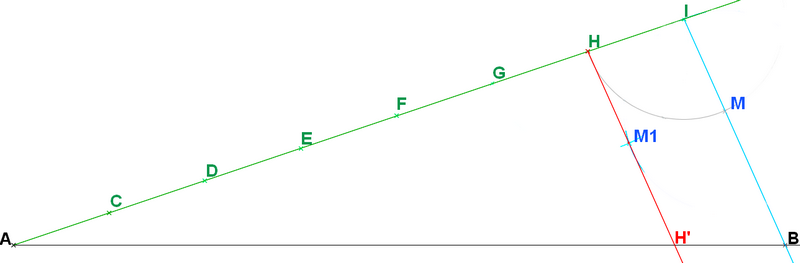
Je pars du même tracé :
* deux demi-droites sécantes [AB) et [AI)
* C, D, E, F, G, H, I sur [AI) tels que AC = CD = De = EF = FG = GH = HI.
Je n'ai pas besoin d'un 8e point J
Donc :
1. Avec le compas je reporte sur [IB) la longueur IH : j'obtiens un point M. J'ai alors IM = IH
2. Depuis H, je trace un arc de cercle de rayon HI.
3. Depuis M, je trace un arc de cercle de rayon MI : il recoupe le précédent en M1.
4. Je trace [HM1) qui coupe [AB] en H'.
Maintenant, je reprends au 2. :
2. Depuis G, je trace un arc de cercle de rayon GH.
3. Depuis M1, je trace un arc de cercle de rayon M1H : il recoupe le précédent en M2.
4. Je trace [GM2) qui coupe [AB] en G'.
Et ainsi de suite...
Veux-tu la preuve de : si un quadrilatère a ses 4 côtés de même longueur alors c'est un losange ?
(J'ai stocké les dessins sur mon disque)
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 31-03-2017 00:15:41
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Re : Géométrie
Bonsoir,
Pour le Point 2, j'ai réussi à vous suivre donc oui ça me va, je vous remercie, j'ai bien compris le pourquoi.
Ce n'est pas naturel de tracer des parallèles avec compas et règle non graduée. De le demander avec compas/règle non graduée rajoute un non-dit que je vais t'expliquer.
J'ignore si tu as vu une leçon traitant des angles et des droites parallèles (1ere page de mon dico).
Oui j'ai vu ça !
Hmmmm...
Je dirais :
la notion de centre de symétrie est liée à la notion de milieu
celle d'axe de symétrie est liée à la notion de médiatrice, donc de milieu et d'angle droit...
Le symétrique d'une droite par rapport à un point est toujours une droite parallèle.
Prenons deux droites parallèles quelconques (ΔΔ) et (DeltaDelta') et un point A sur (ΔΔ) et B sur (ΔΔ').
J'appelle M le milieu de [AB] : Les deux droites sont toujours symétriques par rapport à M, peu importe les positions respectives de A et B l'un par rapport à l'autre...
Prenons encore un point C sur (ΔΔ). En traçant [CM), je coupe (ΔΔ') en D.
D'après la définition, D est le symétrique de C par rapport à M. Et le segment [CD] est le symétrique du segment [AB] par rapport à M.
[AB] et [CD] sont-ils symétriques par rapport à une droite ou à quelle condition le sont-ils ?
Comment les segments [AB] et [CD] peuvent ils être symétriques s'ils se croisent en M ?
Mais je viens de trouver plus rapide et plus simple sans copier un angle.
Mais c'est GENIAL je vous remercie, ENFIN !!! Je ne vais pas vous surprendre si je vous dis que je préfère largement la deuxième méthode ! J'ai essayé de le refaire et c'est vraiment simple.
Voici ce que mon ouvrage me présente comme méthode http://www.cjoint.com/c/GCEv61DsCmU
Et du coup pour mettre en pratique cette méthode, un peu plus loin, dans un autre exercice non corrigé, on m'impose un segment [AB] de 6 centimètres et on me demande de tracer 7 droites parallèles par rapport à une demie droite... et bien je trouve ça encore compliqué, je réessayerai demain...
Oui je suis partante pour la démonstration qu'un losange est bien un carré :-)
Je vous remercie d'être présent depuis plusieurs semaines....
(Je vais commencer des "concours blancs", un jour sur deux, français et math, donc je pense que j'aurai des petites questions par ci par là, sur des choses que nous aurons déjà vues...)
Dernière modification par sarah2811 (31-03-2017 00:18:09)
Hors ligne
#10 31-03-2017 11:47:31
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Bonjour,
Prenons encore un point C sur ($\Delta$). En traçant [CM), je coupe ($\Delta$') en D.
D'après la définition, D est le symétrique de C par rapport à M. Et le segment [CD] est le symétrique du segment [AB] par rapport à M.
[AB] et [CD] sont-ils symétriques par rapport à une droite ou à quelle condition le sont-ils ?
Supposons qu'il existe une droite telle que [CD] soit le symétrique de [AB], autrement dit que le quadrilatère ACBD ait un axe de symétrie.
Prenons le point A.
Quel pourrait être son symétrique ? Réponse (évidente) C, B ou D...
Raah...Encore une gaffe...
Il fallait bien sûr (!) lire :
(...) Et le segment [BD] est le symétrique du segment [AC] par rapport à M.
Supposons qu'il existe une droite telle que [BD] soit le symétrique de [AC], autrement dit que le quadrilatère ACBD ait un axe de symétrie.
Prenons le point A.(...)
Ceci dit ce qui est impossible dans une symétrie centrale (le symétrique d'une droite est une droite parallèle) est possible avec une symétrie axiale...
Soit une droite ($\Delta$) et deux points A et C quelconques placés d'un même côté par rapport à cette droite et tels que (AC) ne soit pas // ($\Delta$).
Soient B le symétrique de A par rapport à ($\Delta$) et D celui de C par rapport à ($\Delta$).
Puisque (AC) n'est pas // ($\Delta$), alors (BD) n'est pas // (AC).
Ces deux droites (AC) et (BC) non parallèles vont se couper sur ($\Delta$)...
Et même si D est le symétrique de C alors je peux dire que C est le symétrique de D !
Donc [tex] A \mapsto B[/tex]
[tex]D \mapsto C[/tex]
D'où [tex](AD) \to (BC)[/tex] et ces deux droites se coupent bien sur ($\Delta$) !!!!.
Tu peux prendre le problème à l'envers : trace un trapèze isocèle ABCD de bases [AB] et [CD]. Ce trapèze possède un axe de symétrie ($\Delta$) qui passe par les milieux de [AB] et [CD]. Les diagonales [AC] et [BD] se coupent en M. M est sur l'axe de symétrie...
Et pourtant [AC] et [BD] sont bien symétriques par rapport à ($\Delta$)...
Preuve expérimentale comme en 6e :
* Dessine ton trapèze sur du papier calque, trace ($\Delta$) et les diagonales [AC] et [BD],
* Plie ton dessin le long de ($\Delta$) et observe par transparence ! [MB] s(applique sur [MA] et [MC] sur [MD].
Ta remarque était juste, mais avais-tu pensé à ce cas ?...
Pigé ?
----------------------------------------------------
Voici ce que mon ouvrage me présente comme méthode http://www.cjoint.com/c/GCEv61DsCmU
Ah... Bin là, ça m'en bouche un coin !!!
Toute la difficulté du procédé consiste justement en le tracé de parallèles.
Dire :
On reporte avec le compas (...) cinq segments consécutifs de longueur arbitrairement choisis. Pas de pb !
Mais, écrire
On trace (BC) puis les parallèles à (BC)...
c'est juste du Yakafokon !!!
Dit comme ça, ce n'est pas une méthode, mais juste un principe : peut-être que leur méthode pour tracer des parallèles est indiquée ailleurs ?
Sinon, pourquoi, moi, j'aurais passé 4 h à me battre avec mon logiciel de dessin géométrique, puis avec un logiciel de retouche d'images pour supprimer les traits en trop ? C'est que je ne pouvais tracer que des cercles pas des arcs de cercle, alors je ne te raconte pas le nombre de fois où j'ai dû recommencer parce que compte-tenu de ces contraintes, je n'avais pas pris les choses dans le bon ordre.
J'aurais dû faire ça, avec instruments réels, puis scanner le résultat.
Démonstration losange
Oui je suis partante pour la démonstration qu'un losange est bien un carré :-)
1. Nan ! Un losange n'est pas un carré... Mais un carré est un losange (et un rectangle !)
2. J'ai proposé de prouver qu'un quadrilatère qui a 4 côtés de même longueur est un losange.
Allons-y.
Soit ABCD un quadrilatère tel que AB = BC = CD = DA.
Puisque AB = AD, alors A appartient à la médiatrice de [BD]
(Théorème réciproque : si un point est équidistant des extrémités d'un segment, alors il appartient à la médiatrice de ce segment)
Rebelote avec CB = CD : C appartient à la médiatrice de [BD].
La médiatrice de [BD] passant par les points A et C, cette médiatrice est (AC).
A ce stade, je sais donc que les diagonales du quadrilatère sont perpendiculaires, et que (AC) passe par le milieu de [BD].
Soit M le milieu de [BD].
Je vais montrer que M est aussi le milieu de [AC].
Variante A
Pour simplifier l'écriture je pose : AB = BC = CD = DA = a et BD = d.
J'ai donc [tex]BM =\frac d 2[/tex].
Que valent AM et CM ?
Le triangle AMB est rectangle en M.
On lui applique le théorème de Pythagore :
[tex]AB^2 = AM^2+BM^2[/tex] donc [tex]AM^2 = AB^2 - BM^2[/tex]
Soit avec mes notations : [tex]AM^2 =a^2 - \frac {d^2}{4}[/tex]
Le triangle CMB est rectangle en M.
On lui applique le théorème de Pythagore :
[tex]BC^2 = CM^2+BM^2[/tex] donc [tex]CM^2 = BC^2 - BM^2[/tex]
Soit avec mes notations : [tex]CM^2 =a^2 - \frac {d^2}{4}[/tex]
Je constate que [tex]CM^2= AM^2[/tex]. Donc CM = AM. Et comme M est sur [AC]. M est le milieu de [AC].
Variante B
(Je reprends ce qui précède la variante A )
J'ai BA = BC . Donc B est sur la médiatrice de [AC]
J'ai DA = DC . Donc D est sur la médiatrice de [AC]
La médiatrice de [AC] est donc (BD). Elle passe par le milieu M' de [AC].
Est-il possible que M et M' soient deux points distincts ?
Supposons que oui. (Raisonnement appelé raisonnement par l'absurde)
Alors cela signifie que (AC) coupe (BD) en M et que (BD) coupe (AC) en M'.
Cela signifie donc que (AC) et (BD) se coupent en 2 points distincts ce qui est impossible.
Donc la supposition est fausse.
Donc, non M et M' ne sont pas deux points distincts, mais un seul et même point : M' = M...
Donc M est aussi le milieu de [AC]
Conclusion
Le quadrilatère ABCD dont les diagonales {AC] et [BD] ont le même milieu M est donc un parallélogramme.
Or AB = BC.
Donc le parallélogramme ABCD qui a deux côtés consécutifs de même longueur est un losange.
--------------------------------------------------------------------
Pour ma deuxième méthode de tracé de parallèles, je pouvais prendre un point M n'importe où sur [IB] :[tex] HI \neq IM.[/tex] Je n'aurais pas obtenu un losange mais simplement un parallélogramme.
J'aurais ensuite décrit le tracé ainsi :
1. Tracer un arc de cercle de centre H et de rayon égal à IM.
2. Tracer un arc de cercle de centre M et de rayon égal à IH.
3. Les 2 arcs de cercle se coupent en M1.
4. La droite (HM1) coupe le segment [AB] en H' qui est un des points cherché.
Puis
1. Tracer un arc de cercle de centre G et de rayon égal à IM.
2. Tracer un arc de cercle de centre M1 et de rayon égal à IH.
3. Les 2 arcs de cercle se coupent en M2.
4. La droite (GM2) coupe le segment [AB] en G' qui est un des points cherché.
On aurait continué avec :
1. Tracer un arc de cercle de centre F et de rayon égal à IM.
2. Tracer un arc de cercle de centre M2 et de rayon égal à IH.
etc...
Quel avantage présentait le losange sur le parallélogramme ?
Il n'y avait qu'un seule valeur du rayon puisque HI = IM.
Et alors ?
Alors, je n'ouvrais mon compas qu'une seule fois tandis qu'avec le parallélogramme, j'avais deux manipulations à chaque fois...
Je te présente ci-dessous même une variante de 2e méthode et elle fonctionne de la même façon que tu aies choisi la construction du parallélogramme ou du losange...
Encore plus rapide (moins d'utilisation du compas) !
Dès le moment où tu as obtenu le point M1, tu traces la droite (MM1) qui se trouve être parallèle à (AI).
Il te suffit alors de garder l'ouverture de compas égale à la longueur HI et sur (MM1) à partir de M1, de reporter cette longueur pour trouver les points M2, M3, M4...
Cela fait, les intersections des droites (GM2), (FM3), (EM4)... te donneront les points G', F', E'... cherchés
Tu as reproduit sur (MM[tex]1[/tex]) ce que tu as déjà fait sur [AI) mais en partant de la fin...
@+
[EDIT] Après relecture, je m'avise que j'ai écrit
je pouvais prendre un point M n'importe où sur [IB] : [tex] HI \neq IM.[/tex]
N'importe où... Donc en particulier en B !!!
De plus en plus court :
1. Tracer un arc de cercle de centre B et de rayon égal à IH.
2. Tracer un arc de cercle de centre H et de rayon égal à IB
3. Ces deux arcs se coupent en M1
4. Tracer la droite (BM1)
5. Sur (BM1) à partir de M1, reporter 6 fois la longueur IH pour obtenir les points M2, M3.... M6
6. Tracer alors les droites (HM1), (GM2)... (CM6) coupant respectivement le segment [AB] en H', G' ... C' qui sont les points cherchés...
Il n'empêche que tu devrais apprendre à reproduire un angle avec règle et compas... ;-))
Dernière modification par yoshi (31-03-2017 12:14:25)
Arx Tarpeia Capitoli proxima...
Hors ligne
#12 03-04-2017 23:54:48
- sarah2811
- Membre
- Inscription : 17-01-2017
- Messages : 59
Re : Géométrie
Bonjour,
D'où (AD)→(BC)(AD)→(BC) et ces deux droites se coupent bien sur (ΔΔ) !!!!.
Tu peux prendre le problème à l'envers : trace un trapèze isocèle ABCD de bases [AB] et [CD]. Ce trapèze possède un axe de symétrie (ΔΔ) qui passe par les milieux de [AB] et [CD]. Les diagonales [AC] et [BD] se coupent en M. M est sur l'axe de symétrie...
Et pourtant [AC] et [BD] sont bien symétriques par rapport à (ΔΔ)...
Preuve expérimentale comme en 6e :
* Dessine ton trapèze sur du papier calque, trace (ΔΔ) et les diagonales [AC] et [BD],
* Plie ton dessin le long de (ΔΔ) et observe par transparence ! [MB] s(applique sur [MA] et [MC] sur [MD].
Ta remarque était juste, mais avais-tu pensé à ce cas ?...
Pigé ?
Oui pigé, non je n'avais pas pensé à ceci, merci pour ces démonstrations...
Ah... Bin là, ça m'en bouche un coin !!!
Toute la difficulté du procédé consiste justement en le tracé de parallèles.
Dire :
On reporte avec le compas (...) cinq segments consécutifs de longueur arbitrairement choisis. Pas de pb !
Mais, écrire
On trace (BC) puis les parallèles à (BC)...
c'est juste du Yakafokon !!!
Dit comme ça, ce n'est pas une méthode, mais juste un principe : peut-être que leur méthode pour tracer des parallèles est indiquée ailleurs ?
Sinon, pourquoi, moi, j'aurais passé 4 h à me battre avec mon logiciel de dessin géométrique, puis avec un logiciel de retouche d'images pour supprimer les traits en trop ? C'est que je ne pouvais tracer que des cercles pas des arcs de cercle, alors je ne te raconte pas le nombre de fois où j'ai dû recommencer parce que compte-tenu de ces contraintes, je n'avais pas pris les choses dans le bon ordre.
J'aurais dû faire ça, avec instruments réels, puis scanner le résultat.
Merciiiiiiii pour votre dévouement :-) J'imagine que ça a dû être pénible... Non ils ne font référence à aucune méthode précise, juste à une liste de méthodes permettant de calculer la longueur d'un segment et de tracer le milieu de ce dernier....
1. Nan ! Un losange n'est pas un carré... Mais un carré est un losange (et un rectangle !)
2. J'ai proposé de prouver qu'un quadrilatère qui a 4 côtés de même longueur est un losange
Tout à fait, votre rectification m'a permise de mettre au clair les définitions de ces différentes figures. Et je vous remercie pour votre démonstration que j'ai essayé (et j'y suis parvenue) de reproduire...
Merci pour le développement des autres méthodes, c'est bon je suis rodée (me semble t-il) en construction d'angle avec compas et règle, j'ai reproduis systématiquement vos instructions, et j'ai compris le principe...
Mais, finalement, je viens d'essayer de refaire un exercice mais je coince troooop...
Comment faire la même procédure, sur un segment de 6 cm et avec la consigne qui est celle de le diviser en 7 parties égales avec compas et règle non graduée...
Je vous remercie...
Dernière modification par sarah2811 (03-04-2017 23:56:59)
Hors ligne
#13 04-04-2017 11:23:24
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Géométrie
Bonjour,
Comment faire la même procédure, sur un segment de 6 cm et avec la consigne qui est celle de le diviser en 7 parties égales avec compas et règle non graduée...
Qu'est ce que ça peut faire que ce segment fasse 6, 8, 9, 11, 15... cm ???
Voilà ce que je peux te dire...
Soit un segment [AB] de $n$ cm de long, n étant un décimal positif.
Tracer une une demi-droite [Ax).
Choisir une ouverture de compas,.
Depuis A, sur [Ax, reporter 7 fois l'ouverture de compas : on obtient les points C, D, E, F, G, H, I
Tracer [IB] puis les parallèles à [IB] passant par H, G, F, E, D, C...
Tu te retrouves à utiliser l'une des 3 ou 4 méthodes que je t'ai décrites...
Ce que je viens de te dire te permet de partager un segment [AB] de longueur quelconque en 7 parties égales.
En outre si tu modifies la phrase :
Depuis A, sur [Ax, reporter 7 fois l'ouverture de compas : on obtient les points C, D, E, F, G, H, I en remplaçant 7 par le nombre entier que tu veux et tu appelles les points [tex]A_1,\,A_2\;\cdots\,A_k[/tex] en appliquant la technique de ton choix tu obtiendras sur [AB] les points [tex]A'_1,\,A'_2\;\cdots\,A'_k[/tex] et tu auras partagé ton segment [AB] en k parties égales...
Là, je te crois que tu as succombé à une crise de... foi (ou de confiance en toi).
Il n'y avait pas de changement..
J'ai fait 3 dessins : est-ce que sur ces dessins, [AB] avait toujours la même longueur ? Bien sûr que non, elles étaient prises au hasard... Et pourtant les 3 fois, tu réussissais à partager [AB] en 7 parties égales...
Pas de panique, reprends tes esprits, tout va bien : tu es arrivé à un niveau qui est supérieur à celui de 80 % des candidat(e)s au concours et même des PE en titre...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1