Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#26 16-10-2016 13:41:16
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Re,
le Shapiro-Wilk te dit si tes X sont normaux. S'il rejette cette hypothèse, rien d'anormal, mais rien de grave pour autant. 27 valeurs ?!? On ne va pas loin avec cela.
Le K-S sert à bcp de choses, regarde bien dans les "préférences" la vérification par défaut.
Donne ici tes couples de valeur, on ne sait jamais, on peut avoir une "brillante idée". Explique un peu aussi le contexte (en respectant l'anonymat, bien sûr), c'est la base de tout.
Et enfin, jette un oeil là, c'est le minimum syndical.
@+
Dernière modification par freddy (16-10-2016 13:42:58)
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne
#27 16-10-2016 14:41:21
- Milos
- Membre
- Inscription : 11-07-2013
- Messages : 94
Re : Robustesse d'une régression linéaire
Bonjour Freddy,
J'ai fait ce que tu demandes et cette fois je trouve :
▼OLS Regression
Dependent Variable YPLUSBLANC
N 100 Multiple R 0,991
Squared Multiple R 0,983
Adjusted Squared Multiple R 0,983
Standard Error of Estimate 470,070
Regression
Coefficients B = (X'X)-1X'Y Effect Coefficient Standard Error Std.Coefficient Tolerance t p-Value
CONSTANT 249,373 98,995 0,000 . 2,519 0,013 X 24,568 0,326 0,991 1,000 75,435 0,000
Analysis of Variance Source SS df Mean Squares F-Ratio p-Value
Regression 1,257E+009 1 1,257E+009 5 690,403 0,000
Residual 21 654 624,388 98 220 965,555
Test for Normality
Test Statistic p-Value
K-S Test (Lilliefors) 0,067 0,295
Shapiro-Wilk Test 0,989 0,550
Anderson-Darling Test 0,395 > 0.15* *The p-value cannot be precisely computed.
Durbin-Watson D-Statistic 2,084 First Order Autocorrelation -0,049
Information Criteria
AIC 1 518,344
AIC (Corrected) 1 518,594
Schwarz's BIC 1 526,159
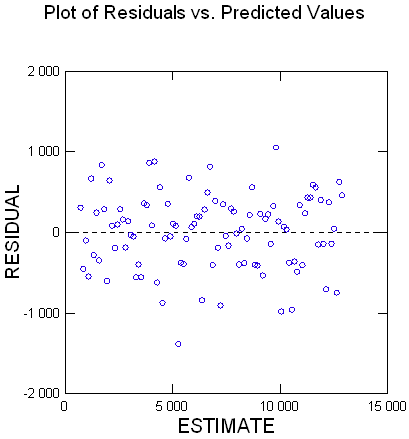
Je me demande, comme dans mes données il y en a une inhabituellement grande alors que dans ce test, elles sont réparties uniformément, si ça aurait un rapport ?
Je fais un essai en la retirant bien qu'elle semble bien ajustée : les x proche de 20 sont nombreux, ceux proches de ce maxi à 94 beaucoup moins.
En tout cas ici, le modèle de départ était 379 + 24x, avec une normale centrée d'écart-type 500, et à l'arrivée les programmes trouvent 254 + 24.6x.
Ceci dit la constante est dans l'intervalle de confiance.
Amitiés,
Hors ligne
#28 16-10-2016 17:17:39
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Re,
intéressant à plusieurs titres.
Pour information, quand je fais ce genre de test avec SAS, même avec seulement 100 couples de valeurs, il retrouve quasiment tout ce que j'ai fabriqué et la manière dont je l'ai fabriqué ! Tu n'as pas un outil statistique assez puissant et fiable à mon avis.
SAS est un outil très puissant sont se sert l'INSEE, l'ENSAE, les entreprises d'assurance et de réassurance, les établissements financiers et toutes celles qui ont besoin de faire des travaux statistiques fiables (car bcp d'argent en jeu derrière).
l'outil R est aussi pas mal fait, c'est un gratuit partitipatif, pas mal de copains s'en servent.
Refais le même test et cette fois-ci, génère X selon une loi normale avec les paramètres que tu veux + un bruit blanc et observe les résultats, notamment le K_S et le Shapiro - Wilk pour la normalité de X.
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne
#29 16-10-2016 19:41:53
- Milos
- Membre
- Inscription : 11-07-2013
- Messages : 94
Re : Robustesse d'une régression linéaire
Bonsoir,
J'ai du me planter, la corrélation s'est complètement effondrée en prenant n avec une moyenne de 40 et un écart type de 10 et le reste égal par ailleurs.
J'ai d'ailleurs eu du mal à fusionner le tableau avec un x normal avec le précédent, j'ai du faire une fausse commande d'autant qu'il me fallait ensuite taper en ligne de commande la nouvelle valeur de "YBLANC".
J'y reviendrai donc, mais je ne serai plus en vacance demain et donc lent..
Amitiés
PS : j'ai regardé les offres de SAS pour amateurs, j'attends la réponse, c'est peut-être prématuré. Dans mon métier, il me semble que l'ATIH utilise SPSS pour les données qu'on leur remonte.
Dernière modification par Milos (16-10-2016 19:49:11)
Hors ligne
#30 16-10-2016 20:03:59
- Milos
- Membre
- Inscription : 11-07-2013
- Messages : 94
Re : Robustesse d'une régression linéaire
Bonsoir,
Je m'y suis repris et cette fois je ne suis pas déçu, au point que je croyais avoir fait une erreur et ai recommencé !
La corrélation calculée est de 1..
Et le modèle parfait, 379, 24*x
Dependent Variable
YPLUSBLANC N 100
Multiple R 1,000
Squared Multiple R 1,000
Adjusted Squared Multiple R 1,000
Standard Error of Estimate 0,000
Regression
Coefficients B = (X'X)-1X'Y Effect
Coefficient Standard Error Std.Coefficient Tolerance t p-Value
CONSTANT 379,000 0,000 0,000 . . .
XBLANC 24,000 0,000 1,000 1,000 . .
Analysis of Variance Source SS
df Mean Squares F-Ratio p-Value
Regression 6 746 515,831 1 6 746 515,831 . . Residual 0,000 98 0,000
Test for Normality
Test Statistic p-Value
K-S Test (Lilliefors) 0,444 0,000
Shapiro-Wilk Test 0,632 0,000
Anderson-Darling Test 20,026 < 0.01* *The p-value cannot be precisely computed.
Durbin-Watson D-Statistic 0,023 First Order Autocorrelation 0,980
Information Criteria AIC . AIC (Corrected) . Schwarz's BIC .
Bref comme disait Boris Vian, il y a un défaut, j'y retourne immédiatement..
@+
Hors ligne
#31 16-10-2016 22:03:07
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Re,
je suis aussi encore en activités, donc pas de souci.
SPSS est peut-être pas mal, on nous l'avait proposé il y a 7 ans pour remplacer SAS, nous avions rejeté la proposition à l'unanimité :-)
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne
#32 17-10-2016 20:07:49
- Milos
- Membre
- Inscription : 11-07-2013
- Messages : 94
Re : Robustesse d'une régression linéaire
Cher Freddy,
En m’y reprenant plus sérieusement, cette fois je n’ai pas oublié d’ajouter le bruit à y, et donc avec les préalables suivants :
XBLANC est simulé avec une loi normale de moyenne 40 et d’écart-type 10
(moyenne mesurée, 40.532, écrat-type 10.877 ; Shapiro-Wilk 0.988, p-value bilatérale 0.532 ; Anderson-Darling 0.312 p-value bilatérale 0.545 ; Lilliefors p-value bilatérale 0.399 ; Jarque-Bera p-value bilatérale et alpha 0.05).
L’erreur ajoutée à YPLUSBLANC = XBLANC*24 + 379 est ERR_N_500 (loi normale centrée 0 et écart-type 100) et j’ai pour ERR_N_500
Moyenne 22.409, écart-type 474.901 ; S-W 0.990. p 0.631, alpha 0.05 ; A-D p 0.576, alpha 0.05 ; Lilliefors p 0.391 alpha 0.05 ; Jarque-Bera p 0.482 alpha 0.05.
J’ai abrégé ci et là en ne donnant pas toutes les valeurs que me donne XLSTAT pour ces tests (genre D et D normalisé pour Lilliefors, etc.)
Aussi bien XLSTAT que Systat me donnent les mêmes valeurs de l’équation
YPLUSBLANC = 560 + 20*XBLANC (donc au lieu de 379 + 24*x) à toutes les décimales près (j’ai arrondi) et les mêmes R^2 (0.176) et ajustés (0.167). Il me semble donc que leur méthode de calcul n’est pas en cause.
Je suppose intuitivement que cette mauvaise corrélation pourrait être en partie liée au fait qu’en prenant X selon une distribution normale, peu de points sont éloignés de la moyenne, alors que la méthode de régression donne sans doute des résultats plus précis quand beaucoup de points en sont distants ? Quand je prenais la répartition uniforme de X depuis 20 à 100 de 5 en 5, la corrélation était bien meilleure.
Il reste la question de la qualité du générateur aléatoire qui est celui de Systat, et que ce programme indique comme étant de type Mersenne Twister. Quand je lis sur cet algorithme, je vois pourtant que cette méthode serait assez valable sauf besoin pointu du genre cryptographie.
Je te joins ci-dessous le graphe des résidus.
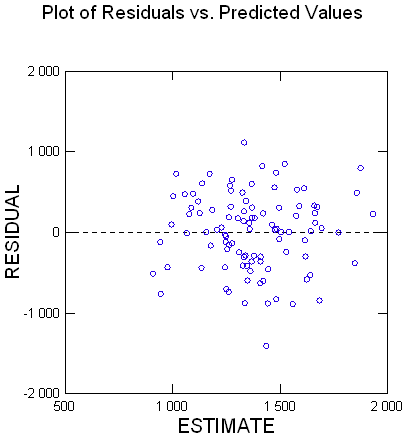
Si tu souhaites toujours que je donne les valeurs d’origine, j’aimerais avec ta permission de les donner en MP, pour éviter de dévier sur des considérations historiques ici, où ce n’est pas ni ne doit être le lieu de ces considérations.
Bien amicalement, @+
Hors ligne
#33 17-10-2016 20:18:12
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Salut,
si ton générateur est du type Mersenne Twister, alors aucun risque de voir des cycles se répéter trop vite. Actuellement, c'est le nec plus ultra en matière de générateur de nombre aléatoire.
OK pour le MP, mais je n'ai vraiment de temps pour travailler dessus. Je regarderai et te dirai.
Du bureau, je ne peux voir ton pgn. Je dois voir chez moi et réfléchir un peu à tes résultats.
@+
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne
#34 18-10-2016 07:08:29
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Re,
ce n'est pas un bruit blanc que t'as mis, c'est un vacarme assourdissant, un boucan d'enfer :-) !!!
Bon, je comprends mieux les résultats, la régression cherche à capturer un fantôme d'une taille inimaginable :-)
Réduis la variance et regarde pour un sigma égal à 2, 1 ou 0.5, valeurs plus réalistes et en rapport avec les paramètres de la loi de X.
Sinon, on peut dire que tes outils sont "corrects", faut juste examiner les valeurs de ta base réduite.
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne
#35 18-10-2016 22:11:32
- Milos
- Membre
- Inscription : 11-07-2013
- Messages : 94
Re : Robustesse d'une régression linéaire
Cher Freddy,
Je recommence donc ce soir, avec un modèle comme conseillé :
>LET ERR_N_500 = ZRN(0,1)
>LET YPLUSBLANC =379 + 24 * XBLANC +ERR_N_500
XBLANC restant tiré au sort avec une loi normale(40,10) et ERR_N_500 rectifiée à ZRN(0,1)
Cette fois les résultats sont trop beaux, j’ai du vérifier l’absence de bourde :
379.286 (ecart type 0.401) et 23.995 (écart-type 0.10)
Avec un R2 de 1.000 ( !)
Et
Lilliefors 0055 p-value 0.590
SW 0.991 p 0.751
Anderson Darlong 0.379 et p>0.15 (non calculable précisément)
Durbin-Watson D 2.233 et F1 AC -0.141
Ci-dessous les résidus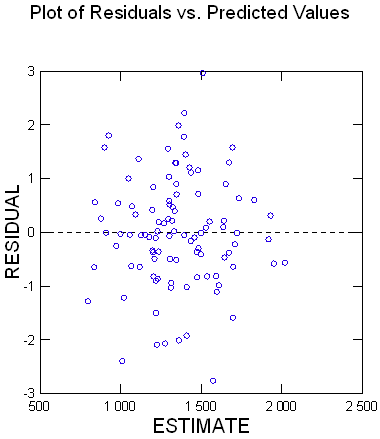
Donc grâce à tes excellents conseils ça marche même trop bien.. :-)
Reste la question de mes 27 couples de départ, même si R^2 n’est pas trop mauvais, pourquoi trouves-tu les résidus mauvais, etc.. quels sont les éléments que je n'ai pas captés ?
Merci en tout cas à toi, amitiés,
Hors ligne
#36 18-10-2016 22:43:01
- freddy
- Membre chevronné

- Lieu : Paris
- Inscription : 27-03-2009
- Messages : 7 457
Re : Robustesse d'une régression linéaire
Salut Milos,
bonne nouvelle !
Le reproche pour tes 27 couples est simple : les résidus ne semblent pas se comporter de manière parfaitement aléatoire, il y un de l'auto-régression sous-jacente. Seul toi sais ce qu'est X et ce qu'est Y, donc qu'il y a peut-être une seconde variable Z indépendant de X à déterminer permettant d'améliorer la qualité de ton ajustement. Ce Z fait partie de ce que tu cherches à expliquer, car c'est dans ta spécialité.
Avant tout chose, qu'elle est l'allure du graphe (X,Y) ? C'est la base de tout travail en la matière.
Tu peux toujours m'adresser ta statistique, je regarderai. Si tu dis que c'est une série chronologique, il faut peut-être regarder de ce côté (intégrer la notion de temps ou de durée).
A te lire !
De la considération des obstacles vient l’échec, des moyens, la réussite.
Hors ligne








