Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 02-09-2016 17:15:14
- Dackou
- Invité
Probleme
Un club de jeux compte 1220 membres qui se repartissent de la manière suivante:792 jouent au bridge, 829 au poker et 618 aux échecs. Mais 213 savent jouer aux trois jeux:206 ne jouent qu'aux échecs et au poker et 320 ne jouent qu'aux cartes.
par contre 806 connaissent jouer au moins deux des jeux.
combien de joueurs ne pratiquent que le bridge, que le poker et que les échecs?
#3 03-09-2016 09:45:48
- Dackou
- Invité
Re : Probleme
salut,
pouvez vous démontrer comment vous avez trouvé cette réponse? Puisque le nombre total des joueurs doit être 1220 joueurs.
merci.
#5 03-09-2016 13:01:14
- jpp
- Membre
- Inscription : 31-12-2010
- Messages : 1 105
Re : Probleme
salut.
@dackou
je m'suis planté . je corrige quand j'ai un moment . sinon pas avant 15 j .
je m'explique :
Il y a 7 catégories de joueurs : EBP , BP , EP , EB , E , B & P
je considère que lorsque tu écris : 320 ne jouent qu'aux cartes , alors 320 = B + P + BP .
et là , j'ai un nombre négatif de joueurs de bridge .
ma réponse précédente , je l'ai donnée en considérant que 320 jouaient au bridge mais aussi au poker .
j'attend donc ta confirmation .
Dernière modification par jpp (03-09-2016 13:32:39)
Hors ligne
#6 03-09-2016 14:13:21
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Probleme
Salut,
Je suis dessus depuis ce matin et j'ai aussi un nombre négatif...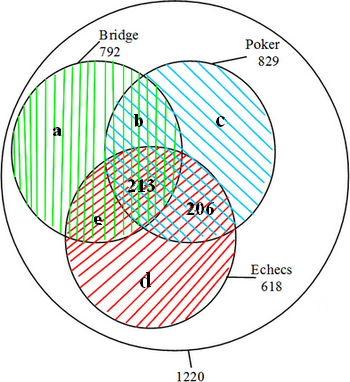
J'ai donc :
a+b+c+d+e+206+213=1220
Soit a+b+c+d+e = 801
Joueurs d'échecs : 618
d+e+213+206 = 618
Soit d+e = 199
D'où a+b+c=801-(d+e) = 602
Mais l'énoncé dit : 320 ne jouent qu'aux cartes...
Or, joueurs de cartes uniquement : vert seul +bleu-vert (pas de rouge)+bleu seul :
Soit a+b+c = 320...
Y a un sérieux souci !
Prenons ça autrement...
806 pratiquent deux jeux au moins, c'est à dire 2 ou 3 mais pas 1 seul, soit b+e+213+206 = 806
soit b+e = 806-419 = 387
Donc bridgeurs :
a+b+e+213 = 792
d'où a = 792 - 213 - 387=192
Poker :
b+c+213+206=829
D'où b+c = 829-419=410
Or a+b+c = 320 dit l'énoncé, il vient donc a = -90
Peut-être y a-t-il confusion, et c'est assez courant, entre au moins et au plus? (pas vérifié)
@+
Arx Tarpeia Capitoli proxima...
Hors ligne








