0.999999=1

bourgelat · 19-03-2014 14:57:14

soit x = 0.999999 avec une infinité de 9
10x = 9.99999999999
10x = 9+x donc 10x - x = 9
9x = 9
x = 1
Cette démonstration du prof de maths de mon fils est pour moi un "sophisme" car une courbe ne se confond jamais avec son asymptote.
de plus, écrire x = 0.999999, c' est admettre que 1/ 1-x est défini donc 1-x différent de zéro.
Parler d'une infinité de 9, c' est parler d' un nombre qui n' existe pas; c' est parler de sa limite .Conceptuellement, où ai je tort?
Je peux écrire f(x) = 1 - 10 puissance -x avec x appartient à N entiers naturels et parler de la limite de cette fonction mais 0.999999 n' est pas un nombre défini.

freddy · 19-03-2014 15:52:29

Salut,

pour une fois, on vous donne la preuve de différente manière en anglais très simple à comprendre ici !

Bonne lecture !

sotsirave · 21-03-2014 01:27:55

Bonsoir

Oui, il faut s’y faire, tout nombre décimal possède 2 écritures chiffrées ( ici en base dix ) avec une infinité de chiffres 0 ou 9 . Et alors ?

Ex : 3, 472 = 3, 472 000 000 … = 3, 471 999 999 …

Mais ce n’est pas pratique pour les opérations.

Ces écritures sont d’un intérêt purement théorique ; en somme une curiosité qui n’est pas indispensable au collège ou au lycée

lambda · 30-09-2014 20:07:23

Bonsoir,

Notre prof nous a étonné avec cette histoire de [tex]0, \bar{9}... = 1[/tex]

Mais, plus étonnant encore, lorsque je reproduis la même méthode avec [tex]x = ...\bar{9}, 0[/tex]

j'obtiens:

[tex]\frac{1}{10}x = ...\bar{9}, 9[/tex]

[tex]\frac{1}{10}x - x = 0, 9[/tex]

[tex]- \frac{9}{10}x = \frac{9}{10}[/tex]

[tex]x = - \frac{9}{10}.\frac{10}{9}[/tex]

[tex]x = - 1[/tex] !!!

Il y a une symétrie qui me surprends !!!

Mais je suis en train de dire que [tex] ...\bar{9}, 0 = -1[/tex] alors que [tex] ...\bar{9}, 0 = \infty[/tex] !!!
Contresens ?

Ciao

lambda · 30-09-2014 21:06:11

Yoshi, je suis fatigué ...

Pourtant, il me semble que c'est bon, non ? (ça commence mal j'ai 2 heures de maths demain matin)

[tex]\frac{1}{10}x−x= ... \bar{9},9 - ... \bar{9},0[/tex]

lambda · 30-09-2014 21:09:11

Où est-ce que ça coince ?
déjà le résultat -1 est bizarre ...

lambda · 30-09-2014 21:12:30

C'est bizarre, en plus il n'y a pas bézef de lignes dans mes calculs

yoshi · 30-09-2014 21:20:26

Re,

Ce que j'avais écrit ne répondait pas à ta question.
J'ai supprimé mon post, alors que tu écrivais.
En relisant, je me suis aperçu de mon hors-sujet, désolé !

Il est clair que ta conclusion est fausse ; je n'avais jamais envisagé ce cas de figure.
Comme ça, je ne vois pas la faute, même si je dirais que la division par 10 de [tex]\overline{9\cdots 999}[/tex] me paraît suspecte...

J'y réfléchirai...
Pas de réponse ce soir : le soir, je dis trop de bêtises.

@+

lambda · 30-09-2014 21:24:31

Ok, il faudra que je fasse attention avec les règles de calculs pour les réels (le premier chapitre de l'année aïe aïe)
À plus tard, j'en parle à mon prof de maths demain

yoshi · 30-09-2014 21:58:25

Bonsoir,

Raaaah... J'avais dit pas ce soir, mais ça me titille
Soit la suite [tex](u_n)[/tex] de terme général [tex]u_n=10^n-1[/tex] et la suite [tex](v_n)[/tex] telle que [tex]v_n=\frac{u_n}{10}[/tex]
avec [tex]n \in \mathbb{N}[/tex]
Je pose :
[tex]w_n=u_n-v_n=10^n-1 -\frac{10^n-1}{10}=\frac{9(10^n-1)}{10}[/tex]

Là pas d'erreur en jouant avec l'infini (dans tous les cas, ce genre de jeu demande de bien savoir ce qu'on fait), je ne l'ai pas utilisé..
Maintenant, que se passe-t-il quand on fait tendre n vers +oo ?

Ce soir, je n'ai pas vraiment le courage de continuer...

@+

lambda · 01-10-2014 13:32:11

Salut,

mon prof (et ses collègues peut-être) vont chercher de leur côté
en attendant, j'essaie de comprendre ta démarche

Ciao

yoshi · 01-10-2014 13:36:39

Re,

Je confirme que ta division est suspecte.
Si tu divises un nombre différent de 0 par 10, tu dois obtenir un nombre inférieur.
Toi tu obtiens un nombre supérieur de 0,9...
Y a un os dans le potage...

D'autre part, qu'est-ce que l'infini divisé par 10 ? L'infini...

Pas eu le temps de poursuivre (et on peut pas répondre à ça d'un simple claquement de doigts) : je suis en plein dans la programmation...

@+

lambda · 01-10-2014 14:21:47

Oui tu as raison : faire des opérations usuelles pour les réels sur l'infini n'a aucun sens, car l'infini en soi n'est pas un nombre, mais une notion, idée ...

yoshi a écrit :

Si tu divises un nombre différent de 0 par 10, tu dois obtenir un nombre inférieur.
Toi tu obtiens un nombre supérieur de 0,9... (tu voulais dire [tex]... \bar{9}, 9[/tex]?
car [tex]\frac{x}{10} = … \bar{9},9 > x[/tex]
avec [tex] x = … \bar{9},0[/tex])

Je confirme ... très bizarre ...

Dernière modification par lambda (01-10-2014 14:33:15)

tibo · 01-10-2014 14:32:06

Salut,

Je dirai que le problème vient du fait de le nombre [tex]...\bar{9}[/tex] n'existe pas.
Quand on écrit [tex]0,\bar{9}...[/tex], on sait que cela représente un réel. L'écriture décimale d'un réel peut comporter une infinité de chiffres après la virgule, mais la partie entière d'un réel a forcément une écriture décimale finie.

Si je reprend la suites de Yoshi [tex]u_n=10^n-1[/tex], quand [tex]n[/tex] tend vers l'infini on a [tex]u_n[/tex] qui tend vers l'infini.
Donc, noter [tex]x=\lim_{n\rightarrow +\infty} 10^n-1= "+\infty"[/tex] me parait déjà bien douteux, mais en plus effectuer des calculs tels que [tex]\frac{1}{10}x = ...\bar{9}, 9[/tex] ou [tex]\frac{1}{10}x - x = 0, 9[/tex] ne peut conduire qu'à un truc faux.

lambda · 01-10-2014 14:37:03

tibo a écrit :

Quand on écrit [tex]0, \bar{9}...[/tex] , on sait que cela représente un réel. L'écriture décimale d'un réel peut comporter une infinité de chiffres après la virgule, mais la partie entière d'un réel a forcément une écriture décimale finie

Voilà le problème ! Un problème de définition ...

Merci tibo !

yoshi · 01-10-2014 14:52:28

Re,

@tibo
Partie entière finie.
Merci, ça m'avait échappé...
Alors, comment se passe ton passage derrière le miroir ?

tibo a écrit :

Donc, noter [tex]x=\lim_{n\rightarrow +\infty} 10^n-1= "+\infty"[/tex] me parait déjà bien douteux,

C'est d'autant plus vrai que cette suite n'a pas de limite : elle est croissante mais n'est pas bornée.
[tex]\forall M \in \mathbb{R}; \;\exists n \in \mathbb{N},\; 10^n-1>M[/tex]

Evolution de w_n pour n de 1 à 60 :

8.1
89.1
899.1
8999.1
89999.1
899999.1
8999999.1
89999999.1
899999999.1
8999999999.1
89999999999.1
899999999999.1
8999999999999.1
89999999999999.1
899999999999999.1
8999999999999999.1
89999999999999999.1
899999999999999999.1
8999999999999999999.1
89999999999999999999.1
899999999999999999999.1
8999999999999999999999.1
89999999999999999999999.1
899999999999999999999999.1
8999999999999999999999999.1
89999999999999999999999999.1
899999999999999999999999999.1
8999999999999999999999999999.1
89999999999999999999999999999.1
899999999999999999999999999999.1
8999999999999999999999999999999.1
89999999999999999999999999999999.1
899999999999999999999999999999999.1
8999999999999999999999999999999999.1
89999999999999999999999999999999999.1
899999999999999999999999999999999999.1
8999999999999999999999999999999999999.1
89999999999999999999999999999999999999.1
899999999999999999999999999999999999999.1
8999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999999999999999.1
8999999999999999999999999999999999999999999999999999999999.1
89999999999999999999999999999999999999999999999999999999999.1
899999999999999999999999999999999999999999999999999999999999.1

@+

lambda · 01-10-2014 16:17:29

Je suis pas le seul à m'y intéresser ...

regarde ,

De nouvelles découvertes et des solutions apportées à des questions mathématiques n'ont pas toujours été faites par des mathématiciens qui en ont fait leur profession. À travers l'histoire, les mathématiques ont fait des progrès en partie grâce au travail d'amateurs. Notre discussion sur [tex]0, \bar{9}...[/tex] offre une parfaite opportunité pour voir l'un de ses cas
Anna Mills (écrivaine américaine et enseignant l'anglais ; 1975 - ) fut encouragée à faire des découvertes semblables à celle qui est donnée concernant le nombre [tex]0, \bar{9}...[/tex] Lorsqu'elle considéra l'entier naturel infiniment grand [tex]... \bar{9}, 0[/tex] elle fut surprise lorsque son analyse prouva que [tex]... \bar{9}, 0 = -1[/tex] ! Elle étaya son résultat en montrant que le nombre [tex]... \bar{9}, 0[/tex] résout les équations [tex]x + 1 = 0[/tex] et [tex]2x = x − 1[/tex] tout comme le fait [tex]-1[/tex]
Encouragée par son enseignant et son père elle poursuit en ce sens ; Anna contacte Paul Fjelstad (mathématicien américain ; 1929 - ). Fjelstad fut capable de déterminer que la découverte visiblement absurde d'Anna [tex]... \bar{9}, 0 = -1[/tex] est, en réalité, vraie tant que l'on considère des nombres en arithmétique modulaire et des nombres p-adic

Voir : thèse de Fjelstad “The repeating integer paradox” in The College Mathematics Journal , vol.
26, no. 1, January 1995, pp. 11-15 ou Discovering the Art of Mathematics - The Infinite

Je l'ai traduit d'un encadré du livre numérique gratuit Discovering the Art of Mathematics – Calculus trouvé sur la toile,
à télécharger ici

Les mots en italiques étaient entre parenthèses dans le texte en anglais

Mais, que sont les nombres p-adic et qu'est ce l'arithmétique modulaire ?

yoshi · 01-10-2014 16:41:03

Salut,

Tu as donc refait une découverte...
L'arithmétique modulaire, va voir là :
http://www.bibmath.net/dico/index.php3? … hmmod.html

Nombres p-adiques :
http://www.bibmath.net/dico/index.php?a … dique.html
** C'est fou ce qu'on peut trouver sur Bibmath... ;-) **

http://fr.wikipedia.org/wiki/Nombre_p-adique
Gare au mal de tête !

@+

lambda · 02-10-2014 19:50:03

Ok pour l'arithmétique modulaire

Mes calculs sont faux ( je manipule l'infini comme un réel ... )

Sur wikipédia on trouve ceci

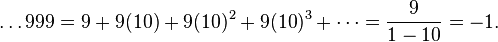
$574d42e645ba95d9651bafec87fd5c7f.png$
(ce qui est plus rigoureux)

l'égalité [tex]... \bar{9} = -1[/tex] serait alors vraie (avec des nombre p-adiques) ...

yoshi · 02-10-2014 20:56:22

Salut,

lambda a écrit :

l'égalité [tex]... \bar{9} = -1[/tex] serait alors vraie (avec des nombre p-adiques) ...

Tu as fait toi même dans ton post précédent cette citation :

[tex]... \bar{9} = -1[/tex] est, en réalité, vraie tant que l'on considère des nombres en arithmétique modulaire et des nombres p-adic

Ci-dessous on joue en arithmétique modulaire : c'est le théorème des restes chinois.
Utilisation du théorème des restes chinois
Explication très vaste :
ici (Wikipedia)

Je m'étais amusé à programmer ça en Python 2.6, ici :
http://www.bibmath.net/forums/viewtopic … 022#p15022

Pour le faire fonctionner en 3.4
1. Remplacer raw_input par input tout court
2. Remplacer les print par par print() qui est devenu une fonction
Ainsi on n'écrit plus (par exemple) print a,b,c mais print (a,b,c)
Je le transformerai un de ces jours...

@+

lambda · 02-10-2014 21:09:02

yoshi a écrit :

"l'égalité [tex]...\bar{9}=−1[/tex] serait alors vraie (avec des nombre p-adiques) ..."
Tu as fait toi même dans ton post précédent cette citation :
"[tex]...\bar{9}=−1[/tex] est, en réalité, vraie tant que l'on considère des nombres en arithmétique modulaire et des nombres p-adic"

Je me répète mais c'est pour une raison simple : il est difficile d'accepter que cette égalité soit vraie, c'est contre-intuitif (d'ailleurs j'aurais pu tomber dans un canular : sur internet, on ne sait jamais). Cette deuxième trouvaille vient confirmer l'encadré que j'ai traduit : l'information a des chances d'être vraie.

Par contre la symétrie entre [tex]0,\bar{9}...=1[/tex] et [tex]...\bar{9}=−1[/tex] est étonnante : il doit bien y avoir une raison

Il est mignon ton jeu !

Dernière modification par lambda (02-10-2014 21:24:50)

gatha13600 · 09-10-2015 21:00:58

Bonsoir à toutes et à tous.
Visiblement, c'est un problème qui intéresse ou a intéressé beaucoup de monde.
Je n'ai pas trouvé de réponse fondamentale.
Merci à tous d'avoir accueilli cette conjecture, et je regrette amèrement l'absence de Nerosson qui se serait volontiers dans la bataille.
En fait, la question devient :
Jusqu'où les mathématiques ont-ils réponse à tout?
Et, comme le présente C. Villani, jusqu'où le monde est-il mathématisable?

PointMathematique314 · 10-10-2015 11:43:02

Bonjour

Oui l'égalité [tex]\bar{9}=−1[/tex] est étonnante mais il y a "pire" :

[tex]1+2+3+4+...=-1/12[/tex]
une somme de nombre positif qui donne un résultat négatif !

pour la démo c'est ici :
https://sciencetonnante.wordpress.com/2 … 34567-112/

C'est Euler qui utilisait ce genre de résultat.
Et pour trouver une explication et bien il disait en gros que lorsqu'on "dépassait plus l'infini on se retrouvait en moins l'infini."
C'est une explication peu convaincante mais pas si stupide, un mathématicien faisait l'analogie avec la pente d'une droite que l'on fait "pivoter" : lorsqu'on arrive à + l'infini on bascule bien vers moins l'infini.

Alors oui on peut obtenir des résultats étonnants en maths surtout quand on fait des opérations avec l'infini.

C'est le cas aussi avec les ensembles infinis : par exemple [tex]\mathbb{N}[/tex] a une taille infinie notée [tex]\aleph_0[/tex] (et [tex]\mathbb{R}[/tex] a aussi une taille infinie [tex]\aleph_1[/tex] avec [tex]\aleph_1[/tex] plus grand que [tex]\aleph_0[/tex] : déjà on remarque qu'il n'y a pas qu'un seul infini mais des infinis, certains plus grand que d'autres!). On peut démontrer que si on enlève la moitié des éléments à [tex]\mathbb{N}[/tex], par exemple les nombres pairs, on obtient un ensemble de taille infini mais qui a la même taille que l'ensemble de départ !

C'est quand même assez étonnant : on enlève la moitié des éléments à un ensemble (non vide) et sa taille ne change pas.

conclusion : il faut se méfier de l'infini (et de l'au delà).

Cordialement
YP

PS : les démonstrations sont très simples à comprendre et très convaincantes (et même géniales), ça doit bien se trouver quelque part sur internet.

Forum de mathématiques - Bibm@th.net

#1 19-03-2014 14:57:14

0.999999=1

#2 19-03-2014 15:52:29

Re : 0.999999=1

#3 21-03-2014 01:27:55

Re : 0.999999=1

#4 30-09-2014 20:07:23

Re : 0.999999=1

#5 30-09-2014 21:06:11

Re : 0.999999=1

#6 30-09-2014 21:09:11

Re : 0.999999=1

#7 30-09-2014 21:12:30

Re : 0.999999=1

#8 30-09-2014 21:20:26

Re : 0.999999=1

#9 30-09-2014 21:24:31

Re : 0.999999=1

#10 30-09-2014 21:58:25

Re : 0.999999=1

#11 01-10-2014 13:32:11

Re : 0.999999=1

#12 01-10-2014 13:36:39

Re : 0.999999=1

#13 01-10-2014 14:21:47

Re : 0.999999=1

#14 01-10-2014 14:32:06

Re : 0.999999=1

#15 01-10-2014 14:37:03

Re : 0.999999=1

#16 01-10-2014 14:52:28

Re : 0.999999=1

#17 01-10-2014 16:17:29

Re : 0.999999=1

#18 01-10-2014 16:41:03

Re : 0.999999=1

#19 02-10-2014 19:50:03

Re : 0.999999=1

#20 02-10-2014 20:56:22

Re : 0.999999=1

#21 02-10-2014 21:09:02

Re : 0.999999=1

#22 09-10-2015 21:00:58

Re : 0.999999=1

#23 10-10-2015 11:43:02

Re : 0.999999=1

Réponse rapide

Pied de page des forums