Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 21-11-2012 15:48:21
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Distances égales
Bonjour,
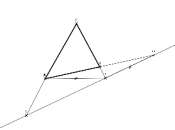
Soit un triangle ABC. On se donne un point M sur la droite (AC) et on veut construire une droite passant par M qui coupe la droite (BC) en un point P et la droite (AB) en un point Q tels que PA=PQ. Il est demandé d'effectuer la construction "à la règle et au compas".
Ce problème de géométrie est très difficile. On peut commencer par une approche analytique
Hors ligne
#2 22-11-2012 13:39:38
- jpp
- Membre
- Inscription : 31-12-2010
- Messages : 1 105
Re : Distances égales
salut.
@totomm . es tu sûr que P est sur (BC) & Q est sur (AB) pour avoir PA = PQ . parce que je vois mieux en permutant les points P & Q .
Peux - tu amener un petit dessin pour mieux comprendre ?
Hors ligne
#3 22-11-2012 15:08:09
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Hors ligne
#4 22-11-2012 18:21:57
- jdec
- Invité
Re : Distances égales
Bonsoir,
Facile !! :-))
Je choisis Q sur (AB), P est l'intersection de la médiatrice de [AQ] avec (BC)
puis M intersection de (PQ) avec (AC)
Mais cela ne donne qu'un exemple... :-((
#5 22-11-2012 21:02:02
- jpp
- Membre
- Inscription : 31-12-2010
- Messages : 1 105
Hors ligne
#6 23-11-2012 11:36:13
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Re : Distances égales
Bonjour,
La réflexion dont jdec se réjouit au post #4 peut être exploitée, mais en laissant M choisi fixe....
La solution complète sera publiée ultérieurement : Une première approche fructueuse est certainement de déterminer le lieu de P quand Q parcourt (AB) en ne conservant que la contrainte PA=PQ
Qu'est-ce qui rend beau un problème de géométrie ?
Cordialement
Hors ligne
#7 27-11-2012 12:43:58
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Re : Distances égales
Bonjour,
Juste pour titiller un peu " l'Entraide (supérieur) " : Comment, à la règle et au compas, marquer l'intersection d'une droite et d'une hyperbole ?
Hors ligne
#8 29-11-2012 16:43:46
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Re : Distances égales
Bonjour,
Comment, à la règle et au compas, marquer l'intersection d'une droite et d'une hyperbole ?
Il y a au moins 2 approches :
1) par les méthodes d'intersection Cône / Plan de la géométrie descriptive
2) Par Inversion car l'hyperbole est le lieu des centres des cercles tangents à deux cercles fixes tangents extérieurement.
Cordialement
Hors ligne
#9 01-12-2012 17:09:23
- jpp
- Membre
- Inscription : 31-12-2010
- Messages : 1 105
Hors ligne
#10 01-12-2012 17:50:58
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Re : Distances égales
Bonsoir,
@ jpp : tout à fait exact. Reste donc à marquer l'intersection P de (BC) avec l'hyperbole (à la règle et au compas).
En caractérisant (géométriquement) l'hyperbole à partir des points A, B et M connus.
Ce n'est pas facile ! Cordialement.
Hors ligne
#11 04-12-2012 18:38:52
- sotsirave
- Membre
- Inscription : 03-11-2012
- Messages : 203
Re : Distances égales
Bonjour
Avec le dessin de JPP , O milieu de [AM], [tex] \vec i[/tex] et [tex]\vec j[/tex] les directeurs normés des droites parallèle et perpendiculaire à (AB), x et y les coordonnées de P / O,i,j, M(a,1) , on obtient xy = a .
P appartient à l'hyperbole équilatère de demi-axe focal [tex]\sqrt{2a}[/tex] de directrice x= [tex]\sqrt a[/tex], de foyer F avec [tex]OF= 2\sqrt a[/tex] etc. .
En remarquant que a est la distance de M à O,j , on peut donc construire les éléments de l'hyperbole et tracer P une intersection de la droite (BC) et de l'hyperbole .
Dernière modification par yoshi (04-12-2012 21:58:36)
Hors ligne
#12 05-12-2012 12:22:35
- totomm
- Membre
- Inscription : 25-08-2011
- Messages : 1 093
Re : Distances égales
Bonjour,
@ sotsirave : l'hyperbole étant bien caractérisée (axe focal y=x avec les vecteurs[tex]\vec i\ et\ \vec j [/tex] que vous avez choisis)
comment tracer effectivement l'intersection de (BC) avec l'hyperbole "à la règle et au compas", tout en s'interrogeant sans doute sur l'utilité actuelle de ces anciennes techniques (voir post #8) ?
@yoshi : merci de rendre bien lisible les textes proposés
Cordialement
Hors ligne
#13 14-12-2012 20:23:23
- sotsirave
- Membre
- Inscription : 03-11-2012
- Messages : 203
Re : Distances égales
Bonjour
Une directrice n'a pas comme équation x = racine carrée de a mais est située à la distance racine carrée de a du centre O de l'hyperbole.
Maintenant la construction de P est classique; soit en utilisant un cercle directeur , le symétrique d'un foyer par rapport à la droite BC et un faisceau de droites, soit en utilisant une directrice un foyer et une homothétie.
La construction quoique délicate ne pose pas de problème.
Hors ligne
#14 07-09-2013 01:29:57
- apoi
- Membre
- Inscription : 09-08-2013
- Messages : 122
Re : Distances égales
salut totomm,
j'ai tombé par hasard dans ce poste . la curiosité m'a poussé d’essayer avec l’exercice après j'ai lu la réponse de jpp dans post#9 et j'ai pas compris . s'il vous plait expliquez-moi ce qu'il a fait , ça sera vraiment gentil et pardon pour le dérangement
Dernière modification par apoi (07-09-2013 01:30:38)
Hors ligne
Pages : 1
Discussion fermée