Forum de mathématiques - Bibm@th.net

Rémy

Invité

Un problème difficile et pourtant intuitivement évident... [Résolu]

Bonjour,

On se place dans  [tex]E={\mathbb{R}}^{n}[/tex] muni de la norme euclidienne et soit  [tex]A\subset E[/tex], A borné.

Pour [tex]\alpha > 0[/tex] on note [tex] U_{\alpha}(X) = \{ y \in E, \exists x \in X, ||x-y|| < \alpha \}[/tex]
En d'autres termes on a  [tex]{U}_{\alpha }\left(X\right)=\bigcup^{}_{x\in X}B\left(x,\alpha \right)[/tex]  (où B(x,a) est la boule ouverte de centre a de rayon a).
Intuitivement, "on part de X et on l'élargit."

On veut montrer que :

[tex]\lim_{\epsilon -> 0} \left( {\sup }_{X\in A} V(U_1 (X) - U_{1-\epsilon} (X)) \right) = 0 [/tex]

Informellement, il s'agit de montrer que la surface de "l'élargissement" de X (avec une distance de 1) est bornée par une borne qui ne dépend pas de X.
(Pour X donné, une application du théorème de convergence dominée à la fonction caractéristique de [tex]U_1 (X) - U_{1-\epsilon} (X)[/tex] montre que ce volume tend bien vers 0... le problème est donc dans le "sup".)

Cette propriété est vraie, intuitivement, parce que le fait qu'on ait affaire à une union de boule de rayon 1 implique que chaque morceau de surface correspond à un volume intérieur minoré... et que donc on ne peut pas "faire rentrer" dans A autant de cette surface qu'on le souhaite.
J'ai pu prouver cette propriété à l'aide d'une (très) fastidieuse (20 pages de Pdf) construction d'une fonction pseudo-injective qui a chaque morceau de la petite bande dont on veut majorer le volume fait correspondre un bout de volume "à l'intérieur"... mais je suis convaincu qu'il y a une manière plus simple.

Si vous avez des idées de pistes de démo, où si vous connaissez des références de trucs qui ressemblent à ce genre de choses et qui seraient susceptibles d'aider... merci :))

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 055

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Salut,

  Je ne comprends pas bien ton sup.
C'est X inclus dans A plutôt que X appartient à A????

Fred.

Rémy

Invité

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Oui tout à fait désolé, c'est le sup pour toute partie X de A.

Rémy

Invité

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

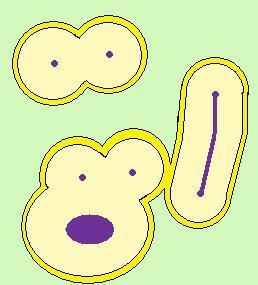
Pour ceux que ça aident, un exemple en dimension n=2 :

Le volume qui nous intéresse est ici l'aire de la zone jaune "d'épaisseur" [tex]\epsilon[/tex].
X est ici représenté en violet.

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 055

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Re-

  J'ai réfléchi un peu (mais pas trop non plus)
et je ne vois pas de solution évidente...
Désolé!

Fred.

Rémy

Membre

Inscription : 14-03-2009

Messages : 5

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Merci. Entre temps j'ai trouvé une piste qui me semble être pas trop biscornue. L'ennui est qu'elle utilise des branches des maths que je connais très mal voire pas du tout donc je ne saurai la formaliser seul :

Le fait que ça marche vient du fait que la "courbure" (qui hélas n'est pas forcément définie en tout point) de la "surface" (la frontière) de [tex]U_1(X)[/tex] est minorée vers "l'intérieur". Ainsi cette surface ne peut se replier assez pour empecher le sup de tendre vers 0...

L'idée est donc la suivante. On considère pour X donné la fonction [tex]f_X[/tex] qui à [tex]a>0[/tex] fait correspondre [tex]f_X(a) = V(U_a(X))[/tex]
Avec quelques théorème sur les intégrales on doit pouvoir obtenir que [tex]f_X[/tex] est dérivable et que sa dérivée en a correspond à la surface (la frontière) de [tex] U_a(X) [/tex]. Majorer cette dérivée en 1 indépendament de X prouve le théorème (c'est même un petit cran plus fort...). Pour ce faire on peut considérer la dérivée seconde (si du moins elle existe... mais il semblerait que oui à priori) et raisonner ainsi: les variation de surface quand on fait varier le rayon a sont localement: soit les variations de surface de l'agrandissement d'une sphère de courbure correspondante au rayon a, soit des variations plus petites puisque la "courbure" "vers l'intérieur" est minorée par cette courbure du cas de la sphère. C'est là que c'est un peu délicat, car il faudrait généraliser la courbure au cas des points singuliers où la surface n'est pas différentiable quelque chose dans le genre... Ou alors faire le raisonnement sur une suite de surface différentiables qui converge uniformément vers notre surface quelque chose comme ça...
Voilà et ensuite en majorant la dérivée première quelque part, on obtient le résultat.

PS: Et avec cette méthode on doit même pouvoir donner une valeur assez bonne de la borne. Intuitivement on maximise la surface en prenant le cas d'une union disjointe de boules de rayon 1. (ce qui correspond au fait que dans cette "piste" on majore la dérivée seconde par ce cas là, finalement)

Dernière modification par Rémy (15-03-2009 00:39:05)

Fred

Administrateur

Inscription : 26-09-2005

Messages : 7 055

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Salut,

  J'avais pensé à une méthode de ce type, mais j'avais l'impression qu'il pouvait
y avoir un problème avec les surfaces de R^2 par exemple dont le bord a une longueur infinie....

Fred.

Rémy

Membre

Inscription : 14-03-2009

Messages : 5

Re : Un problème difficile et pourtant intuitivement évident... [Résolu]

Oui le problème c'est en effet que la surface n'est pas si régulière que ça. En revanche Elle n'a pas de bords puisqu'elle est la frontière d'une union de boules. Localement homéomorphe à R^n-1 en tout point quoi.

... oups c'est une connerie: elle a pas de bords ok, mais elle n'est pas forcément localement homéomorphe à R^n-1 en tout point comme le montre l'exemple X = {(0,0)}, (0,2)} avec rayon=1.

Dernière modification par Rémy (15-03-2009 13:44:21)