Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 07-08-2019 21:29:29
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonsoir Yoshi,
pour l'exo que tu m'as proposé
(x-3) (x-2)
f(x) = ------------
(x-1) (x+2)
1. Quel est son domaine de définition ?
-> je dois avoir x-1 ≠0 et x+2≠0 donc x≠1 et x≠-2
déjà je sais que le plan est partagé en 3 zones
délimitées par les droites d'équations x = -2 et x = 1 ( valeurs interdites )
a) quand x tend vers -2 par valeurs supérieures à -2
(x-3) (x-2) (x-3) (x-2)
-2.09 - 3 = -5.09 -2.09 - 2 = -4.09 -5.09 x -4.09 = 20.81
-2.08 - 3 = -5.08 -2.08 -2 = -4.08 -5.08 x -4.08 = 20.72
-2.07 -3 = -5.07 -2.07 -2 = -4.07 -5.07 x -4.07 = 20.63
-2.06 -3 = -5.06 -2.06 - 2 = -4.06 -5.06 x -4.06 = 20.54
-2.05 -3 = -5.05 -2.05 -2 = -4.05 -5.05 x -4.05 = 20.45
-2.04 - 3 =-5.04 -2.04 - 2 = -4.04 -5.04 x - 4.04 = 20.36
-2.03 - 3 = -5.03 -2.03 -2 = -4.03 -5.03 x -4.03 = 20.27
-2.02 -3 = -5.02 -2.02 -2 = -4.02 -5.02 x -4.02 = 20.18
-2.01 - 3 = -5.01 -2.01 - 2 = -4.01 -5.01 x -4.01 = 20.09
(x-1) (x+2) (x-1)(x+2)
-2.09 - 1 = -3.09 -2.09 + 2 = -0.09 -3.09 x (-0.09) = 0.28
-2.08 - 1 = -3.08 -2.08 +2 = -0.08 -3.08 x (-0.08) = 0.25
-2.07 -1 = - 3.07 -2.07 +2= -0.07 -3.07 x (-0.07)= 0.21
-2.06 -1 = -3.06 -2.06 +2 = -0.06 - 3.06 x (-0.06) = 0.18
-2.05 -1 = -3.05 -2.05 + 2 = -0.05 -3.05 x (-0.05)= 0.15
-2.04 - 1 =-3.04 -2.04 + 2 = -0.04 -3.04 x (-0.04) = 0.12
-2.03 -1 = -3.03 -2.03 +2 = -0.03 -3.03 x (-0.03) = 0.09
-2.02 - 1=-3.02 -2.02 + 2 = -0.02 -3.02 x (-0.02) = 0.06
-2.01 - 1 = -3.01 -2.01 + 2 = -0.01 -3.01 x (-0.01) = 0.03
J'en déduis :
quand je rapproche x de -2, le numérateur (x-3) (x-2) >0 et le dénominateur (x-1) (x+2) > 0
donc f(x) > 0 ..
si je fais tendre x vers -2 par valeurs inférieures , (x-3)(x-2) tend vers 20
et (x-1) (x+2) tend vers 0
donc f(x) est égal à 20 / 0 donc f(x) tend vers + ∞
et je peux dire aussi que f(x) se rapproche de la droite x = -2 et est de plus en plus éloigné de l'axe des x
(j'ai pas pu vérifier avec geogebra , même en faisant des zoom )
`
quand x tend vers -2 de l'autre coté ( je suis en train de faire les calculs mais je pense
que je vais trouver f(x) qui tend aussi vers l'infini
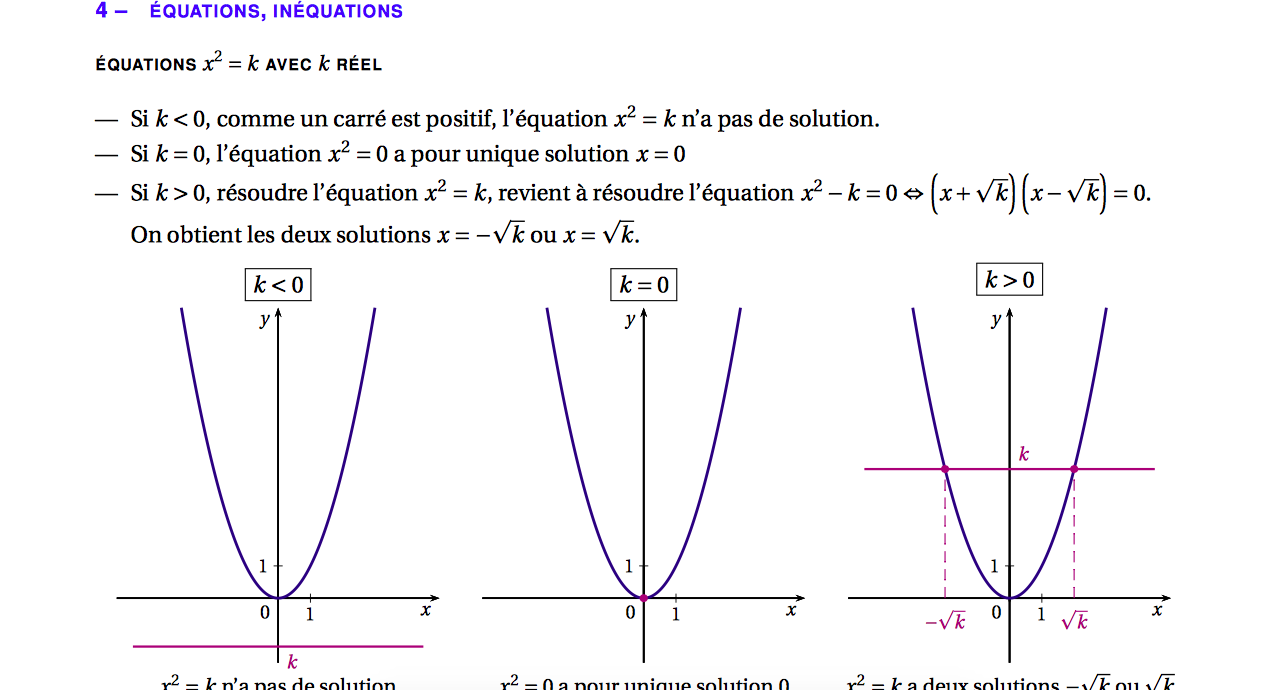
pour la question 2 : quelles sont les solutions de l'équation $f(x) = 0$
voilà, 1 semaine que j'essaie de le faire et tout ce que je sais faire, c'est résoudre des équations du type
$x² = k$ où $k$ est un réel.
(par ex)
si $k = 2$
je passe le 2 de l'autre coté du signe = et j'arrive à x² - 2 = 0 et là je sais factoriser
mais ici, je n'arrive pas à le faire
Peux-tu juste m'orienter mais sans me donner tout le corrigé, j'aimerais trouvé moi-même.
Donne-moi seulement des indications par le biais de questions ( comme tu le fais souvent )
Bonne soirée
à demain
Dernière modification par yannD (07-08-2019 23:08:52)
Hors ligne
#2 08-08-2019 10:18:33
- Volesprit
- Invité
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour, je tombe un peu par hasard sur ce post et je me permets d'intervenir pour signaler que les valeurs supérieures à -2 sont -1.99, -1.98, etc... et non pas -2.01, -2.02 qui sont inférieures à -2
Ensuite pour f(x)=0 (si on parle de la même fonction), que faut-il pour qu'un quotient soit nul? Son dénominateur doit il être nul? Son numérateur doit il être nul? Les deux doivent ils être nuls?
Bon courage
#3 08-08-2019 11:07:31
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour et merci pour votre aide
(x-3) (x-2)
f(x) = --------------
(x-1)(x+2)
il faut que le dénominateur soit nul donc soit x+1 ≠ 0 <=> x≠-1
ou bien x+2 ≠ 0 <=> x≠-2
Hors ligne
#4 08-08-2019 11:08:34
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
une fraction est une division et il est impossible de diviser par 0
Hors ligne
#5 08-08-2019 12:17:42
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
pour la question 2 : quelles sont les solutions de l'équation f(x)=0
voilà, 1 semaine que j'essaie de le faire et tout ce que je sais faire, c'est résoudre des équations du type
x²=k
où k est un réel.
(par ex)
si k=2
je passe le 2 de l'autre coté du signe = et j'arrive à x² - 2 = 0 et là je sais factoriser
mais ici, je n'arrive pas à le faire
Peux-tu juste m'orienter mais sans me donner tout le corrigé, j'aimerais trouvé moi-même.
Donne-moi seulement des indications par le biais de questions ( comme tu le fais souvent
Pourquoi es-tu à ce point "obsédé" par ce type d'équations ?
En 3e, tu en as vu un autre : l'équation produit !
et là je sais factoriser
mais ici, je n'arrive pas à le faire : tu n"as pas l'impression que c'est déjà fait ?
il faut que le dénominateur soit nul
Si j'écris [tex]\dfrac a b=0[/tex] qu'est-ce qui vaut 0 ? (et pourquoi ?)
Sachant cela, pourquoi écris-tu :
il faut que le dénominateur soit nul
??? N'as-tu pas l'impression de te contredire avec le post#4 qui est le seul correct ?
Donc, poursuivons : si $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ et que [tex](x-1)(x+2)\neq 0[/tex], qu'est-ce qui est nul dans la fraction :
$\dfrac{(x-3)(x-2)}{(x-1)(x+2)}$ ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#6 08-08-2019 12:41:38
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Salut Yoshi,
quand j'ai $x^2 - 2 = 0$ c'est déjà factorisé ?
Dernière modification par yannD (09-08-2019 16:19:16)
Hors ligne
#7 08-08-2019 12:51:33
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Salut,
Non bien sûr (tu fais semblant de comprendre de travers ce que j'écris ?), mais le numérateur et le dénominateur proposés, eux, oui...
Je repose mes questions :
1. Si j'écris [tex]\dfrac a b=0[/tex] qu'est-ce qui vaut 0 ? (et pourquoi ?)
2. si $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ et que [tex](x-1)(x+2)\neq 0[/tex], qu'est-ce qui est nul dans la fraction : $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}$ ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 10-08-2019 09:57:44
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour Yoshi,
1.
b = 0 alors
a
---- = 0.
b
Dernière modification par yannD (10-08-2019 09:58:41)
Hors ligne
#9 10-08-2019 10:39:31
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
NOOOOONNNN...
Voilà ce quoi ce qui s'appelle avoir une mémoire sélective !
Nom d'un chat !!!!!
Quand vas-tu mettre dans la tête que :
Un dénominateur ne doit jamais être nul !!!
On ne peut pas diviser par 0.
Démonstration par l'absurde.
Supposons que le quotient du nombre 2 (par exemple) par 0 existe.
Appelons q ce quotient.
Par définition du quotient on a Dividende = diviseur x quotient.
Soit ici :
2 = 0 x q
Or, 0 est un élément absorbant...
Donc 0 x q = 0
En conséquence, on aurait donc 2 = 0.
Ce qui n'a pas de sens.
On ne peut donc pas diviser par 0...
Conclusion : si $\dfrac a b =0$ et que $b\neq 0$, qu'est-ce qui est égal à 0 ?
Maintenant, tu dois pouvoir résoudre l'équation :
$\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#10 10-08-2019 11:52:04
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Salut,
si b ≠ 0
et a/b = 0 alors a = 0
mais pour la question 2. du # 7 : j'y comprends rien
je t'ai scane un paragraphe du cours de cette année sur les résolutions d'équations
et ce type d'équation je sais le faire
(x-3) (x-2)
avec une fraction comme -------------- = 0
(x-1) (x+2)
je n'ai pas (quelque chose ) = 0
ce n'est pas sur la même ligne et je m'y perds
Dernière modification par yannD (10-08-2019 11:53:14)
Hors ligne
#11 10-08-2019 12:04:40
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour,
Je vais te surprendre : le niveau de résolution est classe de 3e, équation-produit.
En effet si :
$\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$,
comme on a [tex](x-1)(x+2)\neq 0[/tex],
il n'y a donc plus qu'à résoudre $(x-3)(x-2)=0$ ^_^...
Tu vois le rapport avec ma question
Si $\dfrac a b =0$ qu'est ce qui vaut 0 ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#12 10-08-2019 17:08:23
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
je me suis dit qu'il y avait 2 équations produit à résoudre
donc j'ai fait (x-3)(x-2) = 0 <=> (x-3) = 0 ou bien (x-2) = 0 donc que x ≠ 2 ou x ≠ 3
et
(x-1) (x+2) ≠ 0 <=> (x-1) ≠ 0 ou bien (x+2)≠0 donc que x ≠-1 ou bien x≠2
Hors ligne
#13 10-08-2019 17:17:26
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
si j'ai bien compris , je dois me dire que f(x) = (x-3)(x-2) / (x-1)(x+2) = 0
si x ≠0
si x≠ 3
si x ≠ 2
Dernière modification par yannD (10-08-2019 17:17:45)
Hors ligne
#14 10-08-2019 18:18:36
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
1. Une seule équation produit :
[tex] (x-3)(x-2)=0[/tex]
2. Je te rappelle que lorsque tu résous une équation, ça peut se terminer de 3 façons différentes :
a) Il y a une ou plusieurs réponses du type $x=...$ (et jamais $x \neq ...$)
b) L'équation est toujours vraie, et l'ensemble des solutions est le domaine tout entier sur lequel on demande de résoudre l'équation
c) L'équation est impossible : il n'y a aucune solution.
3. On te dit de résoudre : $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$
$(x-1)(x-2)$ ne devant jamais être nul, tu as donc à résoudre l'équation dans le domaine $]-\infty\,;\,-2[\,\cup\,]-2\,;\,1[\,\cup\,]1\,;\,+\infty[$
Par conséquent si $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ c'est que $(x-3)(x-2)=0$
En 3e, on t'a fait dire que pour cela :
Il faut et il suffit que x-3=0 ou x-2 =0.
D'où
$x-3=0$ ou $x-2=0$
$\Leftrightarrow$ $\Leftrightarrow$
$x = 3$ $x = 2$
Réponse : Il y a deux solutions x=2 et x= 3
C'est bien ce qu'on t'a appris, non ?
Maintenant, j'aimerais comprendre ce que viennent faire là le $x\neq 0$ (surtout lui), le $x\neq 3$ et le $x\neq 2$....
Parce que vois-tu : Résoudre l'équation $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$,
c'est demander :
Pour quelle(s) valeur(s) de $x$ a-t-on $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ ?
Et que toi tu réponds : on a $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ si $x\neq 0$, $x\neq 3$ et $x\neq 2$....
Je prends $x =5$, on a bien bien $5\neq 0$, $5\neq 3$ et $5\neq 2$ ??
Alors je cherche combien vaut $\dfrac{(x-3)(x-2)}{(x-1)(x+2)}$,
pour $x =5$ :
$\dfrac{(5-3)(5-2)}{(5-1)(5+2)}=\dfrac{2\times 3}{4\times 7}=\dfrac{6}{28}=\dfrac{3}{14}$
Et bien, tu vois ça ne fait pas 0 !!!
Par contre,
pour $x = 3$ ?
$\dfrac{(3-3)(3-2)}{(3-1)(3+2)}=\dfrac{0 \times 1}{2\times 5}=\dfrac{0}{10}=0$ c'est bien 0...
pour $x = 2$ ?
$\dfrac{(3-2)(2-2)}{(2-1)(2+2)}=\dfrac{1 \times 0}{1\times 4}=\dfrac{0}{4}=0$ c'est bien 0...
Alors ???
Tu as un blocage quelque part qui te déstabilise.... Il faut trouver où !
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#15 10-08-2019 18:52:44
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
j'ai répondu :
x ≠ 0
x ≠ 3
x ≠ 2
a / b = 0 si a = 0 donc b ≠0
donc pour f(x) = ((x-3)(x-2)) /((x-1) (x+2))
((x-3)(x-2)) / ((x -1) (x + 2)) = 0 si ((x-3) (x-2) = 0 et
si ((x -1) (x+2)) ≠ 0
Hors ligne
#16 10-08-2019 19:18:48
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
Si je te relis tu as pourtant écrit, post #13
si j'ai bien compris , je dois me dire que f(x) = (x-3)(x-2) / (x-1)(x+2) = 0
si x ≠0
si x≠ 3
si x ≠ 2 :
Tu me dis donc ici que
$f(x)=\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0$ si $x\neq 0$, $x\neq 3$ et $x\neq 2$
Oui ou Non ?
Et je t'ai montré que $f(3)=0$ (et non $\neq 0$), $f(2)=0$ (et non $\neq 0$)
Oui ou Non ?
Et j'en profite pour te redemander pourquoi ce $x\neq 0$ ? (ça, ça m'inquiète beaucoup)
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#17 10-08-2019 20:49:30
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
pour x ≠ 0, je vois ça comme ça :
a / b = 0 alors a = 0 mais aussi b≠0 parce que la division est impossible. D'accord ? (ou pas)
sur le même principe
((x-3)(x-2)) / ((x - 1) (x + 2) = 0 alors ((x - 3) (x - 2)) = 0. D'accord ? (ou pas)
mais aussi il faut que ((x-1) (x + 2) ) ≠ 0
le problème doit venir de la 4e, je me rappelle qu'il y a eut un blocage avec les fractions, ça doit venir de là
Bonne soirée, bonne nuit (à demain )
Dernière modification par yannD (10-08-2019 20:51:01)
Hors ligne
#18 10-08-2019 20:56:41
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
comme il est impossible de diviser par 0 , cela signifie que (x-1) (x+2) ne doit pas être égal à O donc x≠0
ou alors c'est x ≠ 1 par ce que dans ce cas x-1 = 0 et O x (x+2) = 0
Hors ligne
#19 11-08-2019 09:33:26
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
RE,
Je reviendrai sur le reste, mais ça, c'est bien ce que je craignais :
comme il est impossible de diviser par 0 , cela signifie que (x-1) (x+2) ne doit pas être égal à O donc x≠0
Dernière conclusion archi-fausse... Retour à la case départ, je pensais que c'était acquis.
Le dénominateur est $(x-1)(x-2)$. Oui
Il ne doit pas être nul. Oui
Donc $x\neq 0$. Non
$x$ ne doit pas prendre une valeur qui annule le dénominateur...
Cherchons quelles sont ces valeurs :
$(x-1)(x-2)=0\;\Leftrightarrow\; x=1$ ou $x =2$
La réponse corrigée est :
Donc $x\neq 1$ et $x\neq -2$
Dans une étude fonction, si le domaine de définition n'est pas donné dans l'énoncé, on commence par l'établir une fois pour toutes, on en tient compte par la suite, mais (comme ici) on ne recommence pas sans arrêt à le justifier.
Ici on commence par :
[tex]f(x)=\dfrac{(x-3)(x-2)}{(x-1)(x+2)}[/tex]
On doit avoir [tex](x-1)(x+2)\neq 0[/tex], donc [tex]x\neq 1[/tex] et [tex]x \neq -2[/tex].
Le domaine de définition esr
$\mathcal D = ]-\infty \,;\,-2[\;\cup\;]-2\,;\,1[\;\cup\;]1\,;\;+\infty[$ qu'on abrège souvent comme ça : $\mathcal D =\mathbb R \setminus \{-2,1\}$
Par conséquent :
$\dfrac{(x-3)(x-2)}{(x-1)(x+2)}=0\;\Leftrightarrow\;(x-3)(x-2)=0$
Et
$(x-3)(x-2)=0 \;\Leftrightarrow\; x\in\{-2,1\}$
Quant à prétendre que si x = 0 alors (x-1)(x+2) =0 c'est répondre sans avoir réfléchi avant...
Tu vois bien que pour x=0, (x-1)(x+2) vaut [tex]-1 \times 2 = -2[/tex] et pas 0
C'est le Dé-no-mi-na-teur qui ne doit pas être nul, le dénominateur !!!! Pas forcément $x$...
Si $f(x)=\dfrac 1 x,\; f(x)=\dfrac{1}{x^n},\; f(x)=\dfrac{1}{x(x-2)}...$, oui, x ne doit pas être nul (dans le 3e cas il faut aussi éliminer
$x =2$)...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#20 11-08-2019 21:39:33
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 089
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour à vous deux pour une incursion de passage…
@YannD : il me semblait bien il y a quelques temps que cette histoire de division par 0 te pose problème…
Mais les explications de Yoshi sont on ne peut plus claires et tu peux les passer au peigne fin…
A+
Dernière modification par Zebulor (11-08-2019 21:40:36)
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne
#21 12-08-2019 10:36:19
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Boinjour,
Je me demande si ce problème ne serait pas que la manifestation ponctuelle d'un problème plus général, l'arbre qui cache la forêt, quoi...
On va essayer de voir ça.
Quel est l'ensemble des valeurs interdites de f telle que :
a) $f(x)=\sqrt x$
b) $f(x)=\sqrt{-x}$
c) $f(x)=\dfrac{1}{\sqrt x}$
d) $f(x)=\sqrt {x-2}$
e) $f(x)=\sqrt {(x-2)(x+3)}$
f) $f(x)=\dfrac{x-2}{x+3}$
g) $f(x)=\dfrac{\sqrt{x-2}}{x+3}$
h) $f(x)=\sqrt{\dfrac{x-2}{x+3}}$
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#22 12-08-2019 16:22:15
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Bonjour Yoshi,
a) f(x) = √ x
c'est l'ensemble des valeurs négatives qui doit être reriré
b) f(x) = √(-x)
comme je prends l'opposé de x, ici je peux prendre toutes les valeurs des réels compris entre 0 et -∞
Dernière modification par yannD (12-08-2019 16:24:41)
Hors ligne
#23 12-08-2019 17:37:40
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
Pour l'instant, ok !
C'est maintenant que je vais savoir...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#24 12-08-2019 17:55:38
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
a)f(x) = √x
x > 0
b) f(x) = √(-x)
x ≠ 0
1
c ) f(x) = --------
√x
le dénominateur ne doit pas être égal à 0 car a/b = 0 si b≠0
donc : ici √x ≠0
Hors ligne
#25 12-08-2019 20:20:03
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : f(x) = (x-3)(x-2)/(x-1)(x+2)
Re,
D'accord pour $x \neq 0$
Une valeur interdite a est une valeur pour laquelle f(x) n'existe pas...
Donc oui [tex]\sqrt x[/tex] pour <0 n'existe pas...
Et subitement, si je travaille avec $f(x)= \dfrac{1}{\sqrt x}$, alors je peux trouver $\dfrac{1}{\sqrt {-2}}$ (par exemple) ?
Ta réponse est très incomplète...
Tu n'as pas travaillé sur les domaines de définition cette année ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne