Courbes convexes

Vanille · 31-12-2018 08:08:57

Bonjour à tous,

Je suis en train de faire de la microéconomie, et d'étudier les isoquantes de production qui ont une forme convexe décroissante.
Si je ne m'abuse, ce qui caractérise une fonction dont la courbe représentative est convexe est que leur dérivée seconde est positive.

Au niveau du graphique
Quels que soient deux points A et B du graphe de la fonction, le segment [AB] est entièrement situé au-dessus du graphe d'une part et d'autres part une courbe convexe est au dessus de toutes ses tangentes.

En fait ce que j'aimerais beaucoup, c'est comprendre le lien entre le fait que la dérivée seconde soit positive et les conséquences que je viens de citer sur la forme de la courbe convexe.

En quoi le fait qu'une fonction ait une dérivée seconde positive, c'est à dire une dérivée première croissante fait qu'elle a cette forme.

Merci pour votre attention.

Zebulor · 31-12-2018 11:22:31

Bonjour,

On peut désigner par [tex] f [/tex] la fonction étudiée. La dérivée première de [tex] f[/tex] en un point [tex]M(x;f(x))[/tex] notée [tex] f'(x) [/tex] est la pente de la tangente à la courbe de [tex] f[/tex] en ce point. Cette pente correspond à l'angle algébrique formé entre l'axe des abscisses et cette tangente. Supposons que cette dernière coupe l'axe des abscisses en un point A. Cet angle est alors formé par les demi droites [Ax) et [AM).

La dérivée première est aussi le taux d'accroissement de la variable étudiée.

Lorsque la dérivée seconde est positive, la dérivée première est croissante, par conséquent l'angle dont il est question augmente ( toujours en en valeur algébrique) lorsque [tex] x [/tex] augmente. Le taux d'accroissement n'est pas fixe mais s'accroît.

Graphiquement, lorsque x augmente, l'oeil parcourt le graphe de f vers la droite, et cette tangente "se redresse lorsqu'on regarde vers les x croissants".
La fonction carré est un exemple simple à étudier sur n'importe quel intervalle de R. Sa dérivée seconde vaut +2. Pour les x croissants mais négatifs la fonction décroît mais "de moins en moins vite". Pour les x croissants mais positifs la valeur étudiée croît "de plus en plus vite", tout comme l'angle formé par les demi droites [Ax) et [AM).
.

Pour une fonction affine de type [tex] f(x)=a*x+b [/tex], avec a>0 la dérivée seconde est nulle, donc la dérivée première est constante. La pente est donc toujours la même et la forme de la courbe est une droite elle même confondue avec toutes ses tangentes. Le taux d'accroissement est fixe et vaut [tex] a[/tex]. La valeur [tex] f(x) [/tex]croît toujours "à la même vitesse" : lorsque x augmente de 1, [tex] f(x) [/tex] augmente toujours de la même valeur [tex] a[/tex], ce qui n'est pas le cas pour la fonction carré par exemple.

Dernière modification par Zebulor (31-12-2018 16:57:23)

Michel Coste · 31-12-2018 17:32:46

Bonjour,

Un extrait d'un poly ancien :

Une partie $A$ du plan est dite convexe quand elle vérifie la propriété suivante : si $M$ et $N$ sont deux points de $A$, alors le segment $[MN]$ est tout entier contenu dans $A$. Une fonction définie sur un intervalle $I$ est convexe si la partie du plan située au-dessus de son graphe est convexe. Ceci se traduit par la définition suivante :

Définition. Soit $f$ une fonction réelle définie sur un intervalle $I$. On dit que $f$ est convexe quand pour tous $a$, $b$ de $I$, et pour tout $t$ de $[0,1]$, on a
$$f(ta+(1-t)b)\leq tf(a) + (1-t) f(b).$$

La convexité d'une fonction peut se caractériser par le signe de sa dérivée seconde, quand celle-ci existe.

Théorème. Soit $f$ une fonction réelle, deux fois dérivable sur unintervalle $I$. Les propriétés suivantes sont équivalentes :

$f$ est convexe sur $I$,
la dérivée $f'$ est croissante sur $I$,
la dérivée seconde $f''$ est positive ou nulle sur $I$.

Démonstration. Les propriétés 2 et 3 sont évidemment équivalentes.
Supposons vérifiée la propriété 1. Soient $a<b$ deux éléments de $I$. On veut montrer que $f'(a)\leq f'(b)$. Soit $c$ compris entre $a$ et $b$. La convexité de $f$ entraîne
$${f(c)-f(a)\over c-a}\leq {f(b)-f(a)\over b-a}\leq {f(b)-f(c)\over
b-c}.\qquad (*)$$
En effet, on peut écrire $c=ta+(1-t)b$ avec $t\in ]0,1[$, et ces inégalités se réécrivent alors
$${f(ta+(1-t)b)-f(a)\over (1-t)(b-a)}\leq {f(b)-f(a)\over b-a} \leq
{f(b)-f(ta+(1-t)b)\over t(b-a)},$$
ce qui se déduit immédiatement de l'inégalité de définition de la convexité. Quand on fait tendre $c$ vers $a$, le terme de gauche des inégalités $(*)$ tend vers $f'(a)$. Quand on fait tendre $c$ vers $b$, le terme de droite tend vers $f'(b)$. Par passage à la limite dans les inégalités, on obtient donc
$$f'(a)\leq {f(b)-f(a)\over b-a}\leq f'(b),$$
ce qui est ce que l'on voulait.
Réciproquement, supposons la propriété 2 vérifiée, et soit $a<b$ deux éléments de $I$. Soit $c$ compris entre $a$ et $b$. Le théorème des accroissements finis nous dit qu'il existe $d_1\in{]a,c[}$ et $d_2\in{]c,b[}$ tels que
$${f(c)-f(a)\over c-a}=f'(d_1),\qquad{f(b)-f(c)\over b-c}=f'(d_2).$$
Comme $f'$ est croissante et que $d_1<d_2$, on en déduit que
$$ {f(c)-f(a)\over c-a}\leq {f(b)-f(c)\over b-c}.$$
D'où, en posant $c=ta+(1-t)b$,
$${f(ta+(1-t)b)-f(a)\over (1-t)(b-a)}\leq {f(b)-f(ta+(1-t)b)\over t(b-a)},$$
ce qui donne
$$f(ta+(1-t)b)\leq tf(a)+(1-t)f(b).$$
Cette inégalité est vérifiée pour tout $t\in{]0,1[}$, et aussi trivialement pour $t=0$ ou pour $t=1$. Donc $f$ est convexe sur $I$.

Vanille · 31-12-2018 17:46:43

Bonjour Zebulor.
Merci beaucoup d'avoir pris le temps de me répondre.
Malheureusement je me sens un peu frustrée parce que je ne sais pas si j'arrive à avoir une réponse à ma question.
Ce n'est pas du tout la réponse qui ne va pas, parce que je vois bien qu'elle est bien détaillée et rigoureuse, mais je crois que je fais un blocage.
En fait je ne sais pas si tu t'y connais en microéconomie mais en gros on a;
- la fonction de production qui à chaque combinaison de travail et de capital fait correspondre un niveau de production.
C'est donc une fonction de R^2 dans R.
- Les isoquantes de production, qui correspondent aux courbes de niveaux de la fonction de production et qui sont les lignes d'intersection de la surface représentative cette fonction de production avec un plan d'équation z = p qui modélise un niveau de production fixé.
- Donc les isoquantes de production sont représentées sur un repère avec l'abscisse qui représente la quantité de travail utilisé et en ordonnée la quantité de capital utilisé, et les isoquantes relient toutes les combinaisons de travail et de capital qui permettent un niveau de production fixes.
Les isoquantes sont décroissantes car si on augmente la part de travail, on doit réduire la part de capital pour rester sur un niveau de production fixe. La dérivée première négative
Les isoquantes sont convexes. Ceci s'explique par le fait que les combinaisons de facteur capital et travail sont en générale plus productive quand elles sont équilibrées que lorsqu'elle ne le sont pas. Donc plus on aura de travail (c'est à dire plus on sera à droite sur l'axe des abscisses) moins une hausse de l'utilisation du travail devra être compensé par une grande quantité de capital pour rester sur un même niveau de production. On a donc la dérivée première qui est de moins en moins négative, c'est à dire une dérivée seconde positive et donc une courbe convexe.
- On a les droites d'isocoût qui relient toutes les combinaisons de facteur travail et capital permettant un niveau de coût inchangé.
Si on note
pl : le prix du travail
pk ; le prix du capital
l: la variable de la quantité de travail utilisé
k : la variable de la quantité de capital utilisé
CT : le coût total

On a CT( K, L) = L. Pl + K. Pk
et donc les droites d'isocoût ont pour équation K = CT/PK – L. PL/PK

On cherche graphiquement à minimiser les coût pour un niveau de production donné, donc on cherche, sur l'isoquante de production, quelle combinaison de facteur travail et capital permet un niveau de coût minimum.

Et il est admis de dire que cette combinaison qui minimise les coût se trouve au point de tangence de l'isoquante et d'une des courbes d'isocoût.

J'aimerais comprendre pourquoi (en fait je le comprends intuitivement très bien mais ça reste très imprécis dans la mesure où je n'arrive pas à l'expliquer avec des mots rigoureux).

> Qu'est-ce qui fait que l'isoquante n'admet, parmis les droites d'isocoût qu'une seule tangente ?
> Pourquoi une droite d'isocoût qui n'est pas tangente avec l'isoquante modélise soit un coût qui ne permet pas de réaliser le niveau de production souhaité, soit un coût qui n'est pas minime ?
> Pourquoi une droite d'isocoût ne peut pas intercepter qu'une seule fois une courbe convexe (pourquoi c'est forcément 2 fois ou pas du tout ou tangente)

Dernière modification par Vanille (31-12-2018 18:07:23)

Michel Coste · 31-12-2018 18:13:55

En fait, Vanille, tu n'as pas posé la bonne question. Donc ne t'étonne pas d'avoir des réponses qui ne te satisfont pas !

Il faudrait que tu précises plus clairement les propriétés supposées de la courbe isoquante.
C'est le graphe d'une fonction convexe décroissante de $\mathbb R_+^*$ dans $\mathbb R_+^*$ ? Que suppose-t-on sur ses limites en $0$ et en $+\infty$ ?

Vanille · 31-12-2018 18:21:36

Oui je sais que c'est de ma faute, mais j'y vois flou sur ce sujet, et donc j'ai même du mal à comprendre ce que je veux savoir.
D'une façon générale je veux savoir pourquoi le point qui minimise les coût correspond au seul point de tangence entre une des droites d'isocoût et l'isoquante.
De plus mon domaine n'est pas les maths alors je vais avoir tendance à en parler d'une façon plus littérale et économique que mathématiques.
Oui c'est le graphe d'une fonction convexe décroissante de R+ dans R+
La limite en 0 est +l'infini dans la mesure où si la quantité de travail utilisée se rapproche de de zéro il faudra une quantité de plus en plus grande de capital pour permettre au niveau de production de rester constant.
La limite en +l'infini est 0 dans la mesure où si la quantité de travail utilisé de plus en plus grande il faudra une quantité de capital de plus en plus faible pour permettre au niveau de production de rester constant

Dernière modification par Vanille (31-12-2018 18:30:59)

Michel Coste · 31-12-2018 18:24:59

La fonction est-elle strictement convexe ? Est-elle forcément dérivable ?

Vanille · 31-12-2018 18:31:34

Je ne sais pas, on va pas aussi loin dans la rigueur mathématiques dans mon cours.
On se contente de dire que les isoquantes de production ont une forme convexe.

Dernière modification par Vanille (31-12-2018 18:36:50)

Vanille · 31-12-2018 18:32:52

Zebulor · 31-12-2018 19:09:39

Bonsoir Vanille,

ah désolé ! mais rien de grave car les échanges de cette discussion sont profitables pour tous...

Michel Coste · 31-12-2018 19:22:44

La partie du plan au-dessus de l'isoquante, appelons-la $A$, est convexe.
Les droites d'isocoût sont des droites parallèles de même pente négative. Une droite d'isocoût déborde de $A$ sur la gauche (abscisses négatives) et aussi sur la droite (ordonnées négatives). L'intersection d'une droite d'isocoût avec $A$ est donc soit vide, soit un point , soit un segment non réduit à un point (parce que c'est un intervalle fermé borné).
Dans le cas du point, la droite est tangente à l'isoquante en ce poins puisque tous les autres points de la droite sont en dessous de l'isoquante (et qu'on suppose que l'isoquante est le graphe d'une fonction dérivable).
Dans le cas d'un segment non réduit à un point, les deux extrémiités du segment sont les deux points d'intersection de la droite avec l'isoquante (et il n'y en a pas d'autre puidqu'on suppose que l'isoquante est le graphe d'une fonction strictement convexe).

Vanille · 31-12-2018 19:34:40

Zebulor, merci pour ta compréhension, c'est moi qui suis désolée :)

Michel Coste, on touche vraiment du doigt ce que je veux comprendre, je savais qu'il fallait passer par le dénombrement de ces trois cas possibles pour avoir la démonstration de ce que je veux savoir.

je poste quelque chose que j'étais en train d'écrire avant de voir ta réponse

Pour moi la réponse à la question de la minimisation du coût au point de tangence doit se faire en trois parties
- d'une part on doit montrer que l'isoquante admet parmi les droites d'isocoût une unique tangente.
Intuitivement je pense que cette partie devra faire intervenir le fait que les droîtes d'isocoût sont toutes parallèles entre elles
- ensuite on doit montrer que la position relatives des droites d'isocoût peuvent être catégorisées en 3 possibilités : soit une droite d'isocoût coupe 2 fois l'isoquante, soit une droite d'isocoût ne coupe jamais l'isoquante, soit une droite d'isocoût est tangente à l'isoquante
- Pour finir on doit montrer que si la droite d'isocoût ne touche jamais la courbe c'est nécessairement qu'elle ne permet pas d'atteindre le niveau de production souhaité et que si la droite d'isocoût coupe deux dois la courbe c'est nécessairement qu'il existe des droites d'isocoût permettant à la fois un coût plus faible mais aussi de satisfaire le niveau de production souhaité.

Don par rapport à la réponse que tu m'as donnée, pourquoi la droite déborderait sur la gauche uniquement si l'abscisse est négative et sur la droite uniquement sur l'ordonnée est négative : sur ce point je me dis qu'il existe un espace à droite et à gauche de A d'abscisse et d'ordonnée positive (de toute façon en économie on ne raisonne que sur R+)

D'autre part je voudrais justement comprendre pourquoi il n'existe que trois cas possible c'est à dire soit la droite d'isocoût coupe 2 fois, soit est tangente, soit pas du tout.Je crois que j'aimerais une explication plus poussée de ce côté là (pour moi c'est la clé)

Michel Coste · 31-12-2018 19:49:47

pourquoi la droite déborderait sur la gauche uniquement si l'abscisse est négative

Où vois-tu que j'ai écrit ce uniquement ? Il faut lire ce que j'ai écrit, rien que ce que j'ai écrit et pas ce que tu imagines que j'ai écrit !

Le fait central est qu'une droite du plan coupe un ensemble convexe toujours selon un intervalle de cette droite (as tu lu ma première intervention où je donne la définition d'une partie convexe du plan ?). L'argument du débordement pour n'importe quelle droite de pente négative que j'ai donné montre que cet intervalle est nécessairement borné. Il peut être vide, ou réduit à un point.

Dernière modification par Michel Coste (31-12-2018 19:50:17)

Vanille · 31-12-2018 20:00:03

Parce que la phrase "une droite d'isocoût déborde de A sur la gauche (abscisses négatives) et aussi sur la droite (ordonnées négatives)" m'a fait penser que la gauche de A était nécessairement d'abscisses négatives, car pour moi mettre des parenthèse avec juste un groupe nominal à l'intérieur à côté d'une expression revient à donné une équivalence à cette expression;
Exemple :" j'ai mangé des bonbons (à la fraise) " j'aurai tendance à penser que les bonbons mangés sont uniquement à la fraise.
Je suis très attentive à ce que tu écris et je fais du mieux que je peux, maintenant oui je fais peut être des erreurs d'inattention, je m'en suis déjà excusée, mais c'est parce que c'est une question sur laquelle j'ai du mal.

En tout cas merci pour ton aide, et bon réveillon

Michel Coste · 31-12-2018 20:07:06

Les points de la droite d'abscisse ou d'ordonnée négative sont ceux dont on est sûr a priori qu'ils sont en dehors de $A$. Ceci n'exclut pas qu'il y en ait d'autres.
As-tu compris le fait central, à savoir qu'une droite coupe un ensemble convexe fermé du plan en un intervalle fermé, éventuellement vide ou réduit à un point ?

Bonne fin d'année !

Dernière modification par Michel Coste (31-12-2018 20:26:36)

Zebulor · 31-12-2018 20:09:20

Je me permets de m'immiscer très ponctuellement dans cette discussion pour vous souhaitez bon réveillon de même !

Vanille · 31-12-2018 20:46:00

Merci Zebulor :)

"Les points de la droite d'abscisse ou d'ordonnée négative sont ceux dont on est sûr a priori qu'ils sont en dehors de
A. Ceci n'exclut pas qu'il y en ait d'autres." ça je le sais mais la syntaxe de votre phrase "une droite d'isocoût déborde de A sur la gauche (abscisses négatives) et aussi sur la droite (ordonnées négatives)" pouvait à juste titre être interprétée différemment, c'est juste un quiproquo syntaxique entre nous et non de la négligence de ma part.
"une droite coupe un ensemble convexe fermé du plan en un intervalle fermé, éventuellement vide ou réduit à un point" cette phrase je l'ai comprise, mais je cherche à comprendre sa justification, je vais essayer de relire votre premier message mais je ne crois pas qu'on y trouve la démonstration de cette propriété (sauf erreur de ma part).

Dernière modification par Vanille (31-12-2018 20:59:14)

Vanille · 01-01-2019 10:43:04

Bonjour à tous.
Je vous souhaite une très belle année 2019.

Je cherche à montrer que si la droite d'isocoût intercepte la courbe convexe, elle le fait nécessairement 2 fois, ni plus ni moins.

Je sais que c'est un gloubi boulga, et j'espère soit que quelqu'un connaisse la véritable démonstration de cette propriété et me la partage, soit rende ma «démonstration» (si on peut appeler ça comme ça) plus rigoureuse et plus élégante

Lorsque deux courbes décroissantes (droite d'isocoût et isoquante) sont sécantes en 1 point cela signifie que pour toute abscisse située à droite du point d'intersection, les ordonnées de l'une étaient nécessairement plus élevées que les ordonnées de l'autre et qu'à partir du point d'intersection, ce rapport s'est inversé.
Ceci signifie que la courbe qui avait systématiquement des ordonnées supérieures à l'autre a une pente plus négative que l'autre au point d'intersection, puisque pour une même variation de x la variation de y a été plus importante pour la courbe dont l'ordonnée était supérieure avant la variation de x.

Ici la courbe à la pente la plus négative est l'isoquante, car sa limite en 0 est de +l'infini alors que l'ordonnée à l'origine de la droite d'isocoût est de CT/PK, on voit donc bien que c'est l'isoquante qui avait, avant le point d'intersection, des ordonnées supérieures à la droite d'isocoût à abscisse égale.

À présent montrons que lorsque la droite d'isocoût coupe une fois la fonction convexe, elle la coupe nécessairement une autre fois ni plus ni moins.

Preuve qu'elle la coupe une deuxième fois
Par définition la pente d'une droite est constante, or par définition, la pente d'une courbe convexe est de moins en moins négative lorsque l'abscisse tend vers + l'infini.
Il arrive nécessairement un moment où la droite et la courbe vont se recroiser car les points de la droite qui étaient, depuis la première intersection pour une même abscisses associé à une ordonnée supérieure que celle de la courbe convexe, finissent par avoir une ordonnée inférieure pour une même abscisse, car à partir de ce nouveau point d'intersection, pour lequel l'abscisse et l'ordonnée de la droite d'isocoût et de la courbe convexe sont égales, la variation de x entraîne une variation négative plus importante pour la droite que pour la courbe.

Preuve qu'elle ne la coupera plus jamais
A partir de ce point d'intersection, tandis que la pente de la droite restera constante, la pente de la courbe deviendra de moins en moins négative, il n'existera donc plus de possibilité d'intersection.

Merci d'avance à celui qui aura eu le courage de lire ça ^^

Dernière modification par Vanille (01-01-2019 10:56:14)

Michel Coste · 01-01-2019 11:48:58

Bonne année,

Je rappelle le début de mon premier message

Moi a écrit :

Une partie $A$ du plan est dite convexe quand elle vérifie la propriété suivante : si $M$ et $N$ sont deux points de $A$, alors le segment $[MN]$ est tout entier contenu dans $A$.

De ceci on déduit immédiatement que l'intersection d'une droite avec un ensemble convexe dans le plan est un intervalle de cette droite (rappel : un intervalle $I$ d'une droite est un sous-ensemble de cette droite tel que, pour tout couple de points $(M,N)$ dans $I$, le segment $[MN]$ est contenu dans $I$ - autrement dit une partie convexe de cette droite).

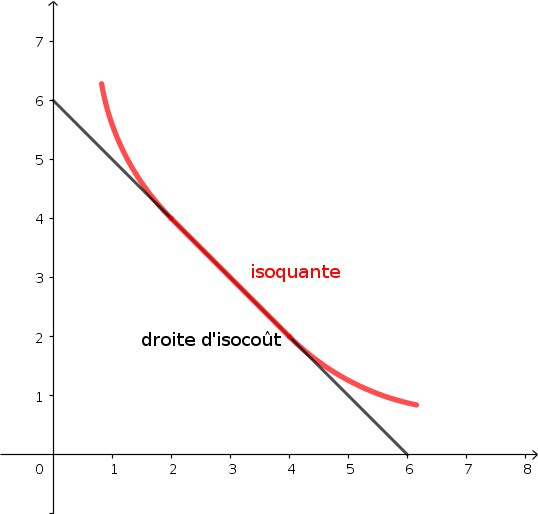
Une petite figure que je laisse à Vanille le soin de méditer : la droite d'isocoût y a tout un segment commun avec l'isoquante.

Vanille · 02-01-2019 15:45:10

D'accord, donc si on part de cette définition de la convexité

Michel Coste a écrit :

Une partie $A$ du plan est dite convexe quand elle vérifie la propriété suivante : si $M$ et $N$ sont deux points de $A$, alors le segment $[MN]$ est tout entier contenu dans $A$.

On a en effet pas à montrer qu'une droite qui coupe une courbe convexe le fait nécessairement une deuxième fois puisque c'est à peut près dans la définition même de la convexité.

Seulement moi, j'ai "compris" pourquoi on modélisait les isoquantes de production par une fonction convexe, à partir de la notion de dérivée.
Le fait que la dérivée seconde soit positive, et donc que la dérivée première soit croissante et donc de moins en moins négative était pertinent économiquement parlant;

Donc ce qui serait intéressant pour moi c'est de comprendre le lien entre le fait que les isoquantes de production sont convexes parce que cela signifie qu'elles sont décroissantes mais de moins en moins rapidement, et le fait qu'elles soient décroissantes MAIS de moins en moins rapidement implique qu'une droite qui couperait une fois la courbe convexe le ferait nécessairement une deuxième fois.

Zebulor · 02-01-2019 16:27:02

Bonjour Vanille et bonne année,

Pour répondre à un de tes posts je n'y connais pas grand chose en économie. Je ne sais pas comment te répondre sur le fond à ton dernier post, mais je crois comprendre que l'approche intuitive de la convexité te parle plus que les équations mathématiques formelles…
La dérivée seconde c 'est le taux d'accroissement du taux d'accroissement lui même.. Pour une droite, ce "taux du taux" est nul..

Dernière modification par Zebulor (02-01-2019 17:01:48)

Michel Coste · 02-01-2019 17:13:01

Vanille, vraiment je ne comprends pas.
1°) J'ai démontré dans le message #2 l'équivalence entre la notion géométrique de convexité et le fait que la dérivée seconde soit positive. As-tu lu ce message ?
2°) J'ai démontré dans le message #11 (avec les "débordements") pourquoi une droite de pente négative coupe la partie du plan au-dessus de l'isoquante selon un intervalle borné ; cet intervalle borné, s'il n'est pas vide ou réduit à un point, a exactement deux extrémités qui sont les intersections de la droite avec l'isoquante (sauf si l'isoquante est confondue avec la droite sur tout l'intervalle, comme le montre le dessin ci-dessus).

Pourquoi reposes-tu toujours les mêmes questions, auxquelles il me semble avoir répondu ? Si tu ne comprends pas un point de ma réponse, questionne-moi dessus. Mais, s'il te plaît, ne fais pas comme si on ne t'avait pas répondu !

freddy · 02-01-2019 17:19:10

Salut,

la convexité de la courbe d'isoproduction est la conséquence de toute l'axiomatique qui sert de support à la théorie microéconomique du producteur et du consommateur. On retrouve son parallèle dans la fonction d'utilité du consommateur.
Sans cela, la théorie de l'équilibre général s'effondre. Cette théorie est établie depuis plus d'un siècle et d'excellents économistes mathématiciens, dont certains nobélisés (Arrow l'américain et Debreu le français par exemple), y ont apporté des contributions décisives pour lui donner ses lettres de noblesse.

Cette convexité est la conséquence de la forme générale de la fonction de production qui doit être homogène de degré un en ses deux facteurs de production (capital et travail) et qui vérifie la loi des rendements décroissants (dérivées partielles premières positives et secondes négatives).

Cette fonction, notée $Y=f(K, L)$, continue et deux fois différentiables, peut être représentée dans le plan (K, L) pour un niveau de production donné. On trace donc des courbe d'isoproduction.

La théorie du producteur stipule que ce dernier cherche à optimiser son profit qui est donnée par le programme ci-dessous :
$\Pi=p\times F(K,L)- (rK + wL)$ où $p$ est le prix de vente unitaire du bien produit, $r$ la rémunération du Kapital et $w$, celle du Labor (travail).

Maximiser son profit revient à chercher les valeurs K et L qui résolvent le programme ci-dessus, avec $p, r, w$ figés.

Les conditions du premier ordre (annulation des deux dérivées partielles premières) donnent :

$p\times F'_K=r$
$p\times F'_L=w$
La concavité du programme fait que ces conditions sont aussi suffisantes.

En combinant ces deux équations, tu obtiens le résultat selon lequel, à l'optimum, le quotient des deux dérivées partielles en K et L est égal au quotient r/w, et ce point est unique. Géométriquement, c'est le point de tangence entre la courbe d'isoproduction et la droite d'isocoût.

Conclusion : si tu trouves deux points d'intersection, cela signifie que tu n'es pas à l'optimum, il faut que tu te déplaces à droite du graphique pour chercher un niveau de production plus élevé avec les mêmes quantité de travail et de capital.

Conseil : si tu veux faire de la microéconomie, fais un peu des maths, le raisonnement littéraire atteint vite ses limites. C'est quand tu auras compris ce que tu fais en maths que tu pourras te lancer dans des explications littéraires.

Bon courage dans tes études, et un bon bout d'an !

Dernière modification par freddy (02-01-2019 17:19:51)

Zebulor · 02-01-2019 18:47:27

Vanille,

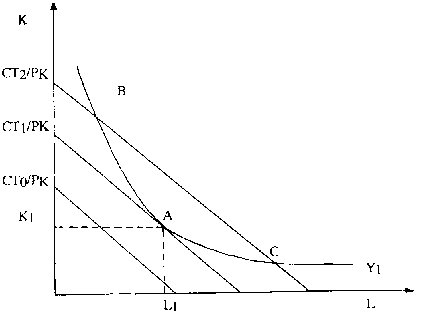
je tente une autre explication à partir de ton post #9 en regardant ce qui se passe entre les points B et C de la figure. Au point B supposons pour fixer les idées que la pente de l'isoquante (courbe convexe) soit -5, soit une dérivée première égale à -5.
En ce même point B la pente de la droite d'isocoût est moins forte, donc la dérivée première en B est supérieure à -5, disons -3.

Déplaçons le regard vers la droite. Comme la dérivée seconde relative à la courbe d'isoquante est positive, sa pente est "de moins en moins négative", passant progressivement de -5 à -4 … puis -3 au point A. En ce même point les pentes de deux courbes sont égales. En nous déplaçant vers la droite, la pente de la courbe d'isoquante continue d'augmenter, les deux courbes se croisent donc nécessairement en C, où la pente de la courbe de l'isoquante vaut par exemple -1.

Dernière modification par Zebulor (02-01-2019 18:50:12)

Michel Coste · 02-01-2019 20:29:51

Petite question : pourquoi la pente de la tangente à l'isoquante va devenir nécessairement plus grande que celle de la droite d'isocoût ?
Ce n'est pas difficile, mais il vaut mieux expliciter ce qui est utilisé ici !

Forum de mathématiques - Bibm@th.net

#1 31-12-2018 08:08:57

Courbes convexes

#2 31-12-2018 11:22:31

Re : Courbes convexes

#3 31-12-2018 17:32:46

Re : Courbes convexes

#4 31-12-2018 17:46:43

Re : Courbes convexes

#5 31-12-2018 18:13:55

Re : Courbes convexes

#6 31-12-2018 18:21:36

Re : Courbes convexes

#7 31-12-2018 18:24:59

Re : Courbes convexes

#8 31-12-2018 18:31:34

Re : Courbes convexes

#9 31-12-2018 18:32:52

Re : Courbes convexes

#10 31-12-2018 19:09:39

Re : Courbes convexes

#11 31-12-2018 19:22:44

Re : Courbes convexes

#12 31-12-2018 19:34:40

Re : Courbes convexes

#13 31-12-2018 19:49:47

Re : Courbes convexes

#14 31-12-2018 20:00:03

Re : Courbes convexes

#15 31-12-2018 20:07:06

Re : Courbes convexes

#16 31-12-2018 20:09:20

Re : Courbes convexes

#17 31-12-2018 20:46:00

Re : Courbes convexes

#18 01-01-2019 10:43:04

Re : Courbes convexes

#19 01-01-2019 11:48:58

Re : Courbes convexes

#20 02-01-2019 15:45:10

Re : Courbes convexes

#21 02-01-2019 16:27:02

Re : Courbes convexes

#22 02-01-2019 17:13:01

Re : Courbes convexes

#23 02-01-2019 17:19:10

Re : Courbes convexes

#24 02-01-2019 18:47:27

Re : Courbes convexes

#25 02-01-2019 20:29:51

Re : Courbes convexes

Pied de page des forums