Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#101 27-11-2018 21:18:18
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
ABCD parallélogramme -> ABCD rectangle quand même abscisse pour le point B et le point C
Hors ligne
#102 27-11-2018 21:20:49
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
ABCD parallélogramme - - > ABCD rectangle.
angle [tex]\widehat{DCB}[/tex] obtu - - > angle [tex]\widehat{DCB}[/tex] droit.
Dernière modification par yannD (02-12-2018 12:12:39)
Hors ligne
#103 27-11-2018 21:31:41
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Donc un parallélogramme qui a un angle droit est un rectangle.
Trace les diagonales du parallélogramme et recommence...
Alors ?
Arx Tarpeia Capitoli proxima...
Hors ligne
#104 27-11-2018 21:34:05
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
je repars de la figure avec l'angle obtu ?
Hors ligne
#105 27-11-2018 21:34:47
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
oui
Arx Tarpeia Capitoli proxima...
Hors ligne
#106 27-11-2018 21:37:00
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Hors ligne
#107 27-11-2018 21:38:47
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Si je t'ai demandé de tracer les diagonales, c'est que ça les concerne, non ?
Recommence...
Arx Tarpeia Capitoli proxima...
Hors ligne
#108 27-11-2018 21:38:55
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
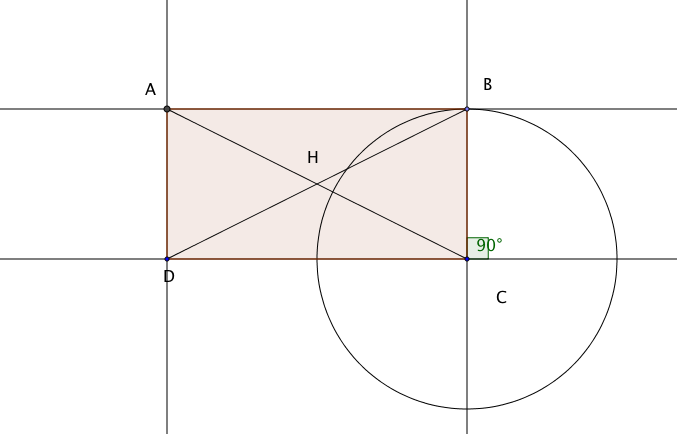
J'ai tracé les diagonales au post #106 et les diagonales [BD] et [AC] ont même milieu.
Dernière modification par yannD (27-11-2018 21:40:54)
Hors ligne
#109 27-11-2018 21:48:17
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Je l'attendais cette réponse !
Et ce n'était pas le cas du parallélogramme ?
Alors recommence et observe mieux : qu'est-ce qui est vrai maintenant avec les diagonales et qui ne l'était pas avec le parallélogramme ?
Arx Tarpeia Capitoli proxima...
Hors ligne
#110 27-11-2018 21:52:59
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Hors ligne
#111 27-11-2018 21:54:49
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
ABCD parallélogramme :
[AC] et [BD] ont même milieu et des longueurs différentes , ce ne sont pas des diagonales équidistantes .
Hors ligne
#112 27-11-2018 21:58:23
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Oui, et maintenant dans le rectangle ?
[EDIt]
A demain...
Dernière modification par yoshi (27-11-2018 22:18:04)
Arx Tarpeia Capitoli proxima...
Hors ligne
#113 27-11-2018 23:37:38
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
oui, à demain merci beaucoup pour l'aide…
Hors ligne
#114 28-11-2018 09:16:11
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Bonjour,
J'attends ma réponse.
Quelques remarques de détail
- diagonales équidistantes : ça ne se dit pas. Équidistant de = situés à la même distance de.
Ex : Tout point situé sur la médiatrice d'un segment est équidistant des extrémités de ce segment.
On prend un segment [AB], sa médiatrice $(\Delta)$ et un point M de cette médiatrice :
M est équidistant de A et de B <=> (distance de M à B)=(distance de M à A) <=> MB = MA
Tu peux dire que les diagonales sont (ou pas) de la même longueur pas qu'elles sont équidistantes.
C'est comme si tu disais dans le cas du parallélogramme ABCD : le côté [AB] est parallèle. (point) ou la longueur AB est. (point)
- quand tu dois comparer parallélogramme et rectangle (bientôt) tu dois te demander ce qui est devenu vrai dans le rectangle et qui ne l'était pas avant avec le parallélogramme.
Donc tu compares les diagonales avant et après : tu as la chance de pouvoir modifier une figure et suivre petit à petit les transformations, donc ouvre les yeux, observe !
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#115 28-11-2018 17:16:25
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
Bonjour
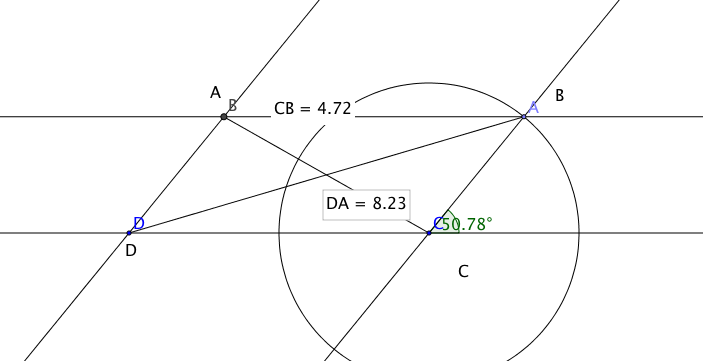
J'ai tracé les diagonales [BD] et [AC] du parallélogramme ABCD et si je pousse le point B vers la gauche avec la souris :
- l'angle DCB diminue
- la distance AC augmente , la distance BD diminue …
Hors ligne
#116 28-11-2018 17:48:06
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
- la distance AC augmente , la distance BD diminue …
C'est vrai, mais tu n'as pas poussé l'observation assez loin, ni la réflexion d'ailleurs.
Au début, l'une est plus longue que l'autre...
Puis la grande diminue et la petite augmente : il y a une question que tu devrais -logiquement - te poser !
Imagine : nous somme sur un escalier, moi, en haut, toi, en bas
Puis je descends et toi tu montes...
Quel événement prévisible va-t-il se produire ?
Alors maintenant, transpose ça aux diagonales : la grande longueur diminue, la petite augmente...
Que va-t-il se produire ?
Arx Tarpeia Capitoli proxima...
Hors ligne
#117 28-11-2018 17:52:21
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
grande longueur = petite longueur
Hors ligne
#118 28-11-2018 18:40:18
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Enfin !
Donc propriétés supplémentaires à ajouter au parallélogramme pour obtenir un rectangle :
- 1 angle droit. Pourquoi 1 seul ? Parce qu'il est facile de prouver que s'il y en a 1, les 3 autres sont aussi des angles droits.
ou
- Des diagonales de même longueur.
Je change de machine (je suis sur mon portable et il n'a pas Geogebra), je bidouille et je reposte pour le losange...
Arx Tarpeia Capitoli proxima...
Hors ligne
#119 28-11-2018 19:16:10
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
ok, donc là, j'ai conjecturer avec un logiciel dynamique (ici, c'est Geogebra) que pour passer d'un parallélogramme à un rectangle , et bien j'ai 2 propriétés en plus : 1 angle droit et diagonales égales. Conjecturer c'est ce que l'on fait en séance TD, on démontre avec Geogebra, c'est ça ?
Hors ligne
#120 28-11-2018 19:36:15
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Re,
Avec Geogebra, tu ne démontres rien, tu conjectures (tu fais des remarques, des suppositions) et tu vérifies que c'est possible, que c'est probablement vrai à 99 %...
Avec Geogebra, Trace les droites d'équations y=2 et y =-2.
* Sur la première droite, place le point A de coordonnées (0 ; 2)
* Sur la deuxième droite, place le point C de coordonnées (8 ;-2). Renomme-le en C !
* Place le milieu M de [AC] avec l'outil milieu - centre . (Renomme-le M)
Au passage, calcule donc ses coordonnées et vérifie avec celles que te donne Geogebra pour voir si tu te souviens toujours comment faire...
* Sur la première droite, place un point B d'abscisse supérieure à 8, autour de 10 mais avec l'outil Point sur Objet.
* Trace la demi-droite [BM), elle coupe la droite d'équation y =-2. Marque ce point d'intersection. Il se nomme D.
* Trace les segments [BD] et [AD].
On a obtenu un parallélogramme ABCD.
Clique sur la flèche et déplace le point B à droite à gauche. Tu vas t'apercevoir que pour arriver à former un losange, B doit se déplacer vers A.
Si tu arrives à voir quand tu l'as obtenu, c'est bien, sinon le point B a pour abscisse 5 : Geogebra t'indique l'abscisse quand tu déplaces B.
Alors, qu'est-ce que ce losange a de plus que le parallélogramme de départ ? (2 propriétés).
Déplace tant que tu veux et observe bien : cherche les différences entre le parallélogramme de départ et le losange d'arrivée...
Qu'est-ce qui est vrai dans le losange et qui ne l'était pas dans le parallélogramme ?
Rappel :
Que ce soit dans le losange ou le parallélogramme :
- les 4 côtés sont parallèles 2 à 2
- les côtés opposés sont parallèles et de même longueur.
- les diagonales ont le même milieu.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#121 28-11-2018 19:48:53
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
donc , je conjecture, je remarque que je dois arrêter de pousser le point B quand l'angle DCB est un angle droit et après il faut démontrer (par ex).
Hors ligne
#122 28-11-2018 19:57:36
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Oui.
Enfin, c'est plutôt remarquer que l'angle $\widehat{DCB}$ est droit, mais c'est évident : je te rappelle que rectangle vient du latin rectus droi et angulus droit.
Là, ce serait plutôt remarquer que si l'un est droit les autres aussi, donc que parallélo + 1 angle droit suffit.
Par contre, tu pousses B jusqu'au rectangle, tu t'arrêtes et tu regardes les diagonales. Et tu conjectures qu'elles sont égales.
Tu mesures ça avec Geogebra qui te confirmes que à 99%, c'est vrai !
après, place à la démo (Pythagore)...
Autre méthode de construction de mon losange.
Commence par placer un curseur a variant de 0 à 11 avec un incrément de 0.5.
Place les points A(0;2), B(a;2), C(8;-2) et D(8-a;-2)
Trace les segments [AB], [BC], [CD], [DA] et les diagonales [AC]et [BD].
Marque le point d'intersection M des diagonales...
Démarre en poussant le curseur à a = 11.
Maintenant, diminue la valeur de a jusqu'à obtenir un losange.
@+
Dernière modification par yoshi (28-11-2018 20:04:00)
Arx Tarpeia Capitoli proxima...
Hors ligne
#123 28-11-2018 20:06:51
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
Je vais regarder après la 2e construction et je fais d'abord la construction proposée au #120
Geogebra
J'ai directement écrit A = (0,2) et B = (8,-2) dans la barre d'entrée, ainsi je n'ai pas besoin de renommer B en C.
J'ai construit le milieu de [AC] avec l'outil milieu d'un segment, j'ai obtenu un point B et là, j'ai dû renommer en M.
Calcul des coordonnées de M :
A (0;2)
B (8;-2)
xM = (xA + xC) / 2 = (0 + 8) / 2 = 8/2 = 4
yM = (yA + yC) / 2 = (2 + (-2)) / 2 = 0/2
M ( 4;0)
Je jette un oeil sur ma figure, c'est bon !
Dernière modification par yannD (28-11-2018 20:10:05)
Hors ligne
#124 28-11-2018 20:09:53
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Géométrie seconde Translations et Vecteurs
Re,
B = (8,-2) dans la barre d'entrée, ainsi je n'ai pas besoin de renommer B en C.
Sauf que tu ne pourras pas déplacer B !!
Je t'avais écrit :
Sur la première droite, place un point B d'abscisse supérieure à 8, autour de 10 mais avec l'outil Point sur Objet.
Arx Tarpeia Capitoli proxima...
Hors ligne
#125 28-11-2018 20:10:46
- yannD
- Membre
- Inscription : 19-10-2018
- Messages : 1 589
Re : Géométrie seconde Translations et Vecteurs
j'ai pas eu la fin de message…
Hors ligne