Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 18-09-2018 22:02:04
- Jouvin
- Invité
Problème géométrique de 2nde
#2 18-09-2018 22:09:21
- Jouvin
- Invité
Re : Problème géométrique de 2nde
Je vous post un autre lien pour la photo car on vois très mal sur la première.
Merci
photo
#3 18-09-2018 22:13:46
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Bonsoir,
Réponse simple mais assez longue...
Si personne ne s'y est collé, cette nuit, RV demain matin...
Pour moi, c'est tout pour ce soir...
apparemment elle n'a pas vu cela en cours
Désolé, mais c'est un discours entendu des milliers fois...
Et il y a moins d'une chance sur 10000 que ce soit exact...
Dans toute ma carrière, je n'ai croisé qu'une seule fois quelqu'un qui procédait ainsi et ce n'était pas un prof de Maths.
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#4 19-09-2018 09:08:30
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Bonjour,
La première chose à essayer est de construire plusieurs dessins, soit à la main (ça peut se faire à main-levée), soit avec un logiciel comme Geogebra (un must !) ou le petit logiciel de Géométrie du site Geolabo (sans prétention, mais performant quand même et plus simple d'emploi).
1. Je propose donc de construire un segment [AB] de longueur 10 cm. Rien d'affolant... Précision : les deux sont gratuits (et sans virus !).
Il faut bien comprendre que le point M n'est pas fixe : on peut le le poser n'importe où entre A et B
2. Sur [AB], on place un point M, par exemple au milieu de [AB] et de refaire le dessin fourni.
Puis de placer encore deux autres points
* M1 sur [AM] par exemple au milieu de [AM] (AM1=2,5 cm)
* et M2sur [AM1], par exemple à 2 cm de A.
3. Construire avec 3 couleurs différentes le carré et le triangle rectangle.
Observer les 3 positions...
A) Quand on passe du carré AMCD au carré AM1CD puis au carré AM2CD.
C'est à dire quand le point M se rapproche du point A : la longueur AM diminue, diminue, diminue...
Le carré AMCD devient de plus en petit : son aire qui vaut AM², elle aussi diminue, diminue, diminue...
Et quand le point M et le point A ne feront plus qu'un seul point, où seront les 2 autres points C et D ? Que sera devenu le carré ?
Que vaudra son aire ?
Mais si, quand le point M se rapproche du point A, la longueur AM diminue, diminue, diminue..., la longueur ME (ME = AM) diminue aussi...
Et le point E se rapproche du point M. Lorsque le point M aura rejoint le point A (AM=0), le côté [ME] du triangle existera-t-il toujours ?
Et le triangle MBE ? Que vaudra son aire ? Rappel : aire du triangle rectangle= (côté de l'angle droit x 2e côté de l'angle droit)/2
B) Maintenant il faut faire l'analyse inverse. On regarde dans le sens M2 --> M1 --> M : on s'éloigne de A, on se rapproche de B...
La longueur AM augmente, augmente, le carré devient plus grand. Que vaudra AM quand M et D ne seront qu'un seul point ?
Quelle sera alors l'aire de ce carré AMCD quand M et D ne seront qu'un seul point ?
Et le triangle ?
Comme ME = AM, la longueur du côté [ME] augmente aussi...
Par contre la longueur MB diminue, diminue... Combien vaut-elle si M et B ne sont qu'un seul point ? Le triangle est-il toujours visible ?
Quelle est son aire à ce moment là ?
Pour faire ces tracés et ces observations a-t-on besoin d'un cours ?
Poser une question c'est déjà y répondre dit-on..
Alors je réponds : non !
Il faut avoir le réflexe de ne pas s'affoler, de se souvenir qu'il y a 3 verbes fondamentaux à mettre en œuvre : Observer, Comparer, Déduire...
Mais aussi pour s'en servir, soit de penser à faire plusieurs dessins rapides, soit d'utiliser un logiciel de dessin géométrique qui permet de faire un dessin bien sûr, mais aussi de le faire varier, en comme ici en déplaçant un point...
Question 2.
Les notations f(x) et g(x) sont connues depuis la 3e.
Ici les fonctions f sont des relations qui permettent à partir d'une longueur x donnée d'écrire les formules qui calculent les aires du carré (cette formule est appelée f(x) - lire : f de x) et du triangle (cette formule est ici désignée par g(x) - lire : g de x)
Question A)
AB mesure 10 cm. M se déplace sur [AB] : entre quelles valeurs minimum et maximum varie la longueur AM ?
Et comme on a décidé de noter x cette longueur AM. La réponse à ma question donnera la réponse à la question A.
La réponse est attendue sous la forme [tex]mini\leqslant x \leqslant maxi[/tex] ou [mini ; maxi] si cette dernière notation a été vue...
Je m'arrête là pour l'instant.
Inutile de noyer votre fille.
Si elle a compris jusque-là, je poursuivrai, sinon j'attends ses questions (et les vôtres ^_^).
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#5 19-09-2018 09:36:02
- Jouvin
- Invité
Re : Problème géométrique de 2nde
Bonjour je vais lui montrer et je vous redis car moi je suis noyer
#6 19-09-2018 11:16:50
- Jouvin
- Invité
Re : Problème géométrique de 2nde
Voilà ce qu' elle a commencé à dessiner , part elle bien ou pas du tout ?
#7 19-09-2018 12:27:36
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Bonjour,
Oui et non...
Image 1.
Votre fille ne m'a pas lu attentivement
Positions de A et M, et C et D correctes.
Mais j'ai écrit :
Mais si, quand le point M se rapproche du point A, la longueur AM diminue, diminue, diminue..., la longueur ME (ME = AM) diminue aussi...
Et le point E se rapproche du point M. Lorsque le point M aura rejoint le point A (AM=0), le côté [ME] du triangle existera-t-il toujours ?
De plus,
A chaque position du point M correspond (..) et un triangle MBE rectangle en M tel que AM=ME
Dans ce dessin 1, A et M sont confondus, le segment [AM] est réduit à un point...
Quand M se rapproche de A, AM diminue mais ME aussi : ME doit constamment avoir la même valeur que ME...
Donc E mal placé...
Pas besoin d'une autre photo, simplement me dire où est le point E quand M est sur A...
Image 2
Pourquoi le point E est-il aligné avec D et A ??
L'angle [tex]\widehat{MAE}[/tex] n'est pas droit, M n'est pas au milieu de [CE] sur ce dessin...
Image 3 et 4
Oui, j'aurais aimé voir écrite la longueur de ME...
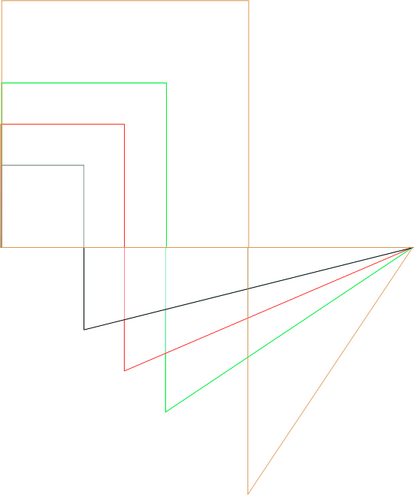
(Image faite via mon traitement de textes...)
@+
.
Arx Tarpeia Capitoli proxima...
Hors ligne
#8 20-09-2018 11:10:13
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Bonjour,
@Au papa, attendant les réactions de sa fille. Toujours noyé ? Pourquoi ?
Qu'est-ce que vous ne comprenez pas jusque-là ?
@A la fille.
Il doit être clair maintenant que M pouvant être n'importe où sur [AB] y compris les points A et B, la longueur AM (notée $x$) peut rendre n'importe quelle valeur de 0 à 10...
Question 1 C
Pour AM = 2 cm, il reste MB=10 -2 = 8 cm et [MB] est un des côtés de l'angle droit du triangle rectangle BME.
L'autre côté qui nous intéresse est [ME].
Et l énoncé dit que ME = AM. Donc ici ME = 2cm.
Voilà de quoi calculer l'aire du triangle rectangle : la formule (BM * ME)/2 dit que l'on calcule simplement la moitié de l'aire d'un rectangle...
Quant au calcul de l'aire du carré AMCD, il ne nécessite que la connaissance du côté du carré. Ici AM = 2 cm.
Question 1. B) Faire de même en prenant AM = 7 cm
Question 2. A partir de cet instant on ne donne plus la valeur de AM, on dit qu'elle vaut une longueur inconnue (=qu'on ne vous donne pas) et qui pour cette raison est traditionnellement désignée par $x$...
Ce qui veut dire qu'au lieu de faire de l'Arithmétique et calculer avec AM = 2 cm ou AM =7 cm, il va falloir utiliser l'inconnue $x$ à la place de ces valeurs et in va faire un peu d'Algèbre...
2) B) De façon simplifiée, au lieu de dire Aire du carré, on va écrire $f(x)$ et au lieu de Aire du triangle on va écrire $g(x)$...
Que vient faire le $x$ dans $f(x)$ et dans $g(x)$ ? Il est là pour dire que ces aires sont calculées en utilisant la valeur $x$, en fonction de $x$...
Donc $AM = x$ et l'aire du carré de côté [AM] étant AM², on va écrire : ... (en utilisant la lettre $x$)
Et ME ? Et bien l'énoncé dit ME = AM, donc on aura $ME=x$
Passons à BM... On a AB = 10 cm, on lui enlève une longueur AM. Pour connaître BM :
* dans le 1.C) on a fait AB-AM =10-2 = 8,
* dans le 1.D) on a fait AB-AM = 10-7 = 3...
Maintenant, on a $AM = x$, donc $BM =10 - x$...
N-B : souvent, à ce stade, on nous pose la question : et ça fait combien $10-x$ ?
Et bien tant qu'on ne sait pas combien vaut $x$, in garde $10-x$.
Tous les calculs maintenant vont se faire en gardant $x$.
On écrit :
(Aire du carré) $f(x) =\cdots$
(Aire du triangle = $\dfrac{ME\times BM}{2})$, donc en utilisant $x$ : $g(x)=\dfrac{\cdots\times (\cdots)}{2}$
Pourquoi y a-t-il des parenthèses ? Parce que sinon il y aura une faute de calcul. En effet BM c'est le résultat de la soustraction de x à 10...
Et la seule façon d'écrire correctement le produit est de mettre $10-x$ entre parenthèses...
J'arrête provisoirement là en attendant une réponse...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#9 20-09-2018 11:58:10
- Jouvin
- Invité
Re : Problème géométrique de 2nde
Bonjour, et merci de suivre mon post, alors juste avant de partir travailler.
Pour la question 1 A) si j'ai bien compris en confondant M avec À il ne restera que le segment ADCEM vers B . Puisque Am= me =ad=dc=cm.
#10 20-09-2018 13:33:57
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Bonjour,
Oui.
Si on déplace M vers A AM diminue et donc ME aussi. Par conséquent, E se rapproche du segment [AB].
Et quand M est arrivé en A La longueur AM vaut 0 et donc ME aussi. Alors A, M, E ne font plus qu'un point...
Et le triangle BMR est complètement aplati sur [AB]
Mais le carré aussi rétrécit : CD diminue, MC diminue, DA diminue : on le voit bien sur le dessin en le regardant de droite à gauche...
Et quand M est arrivé en A, le carré s'est ratatiné et il ne reste plus de lui... qu'un point !
A, M, E, C, D sont tous en A.
Que voit-on donc dans ce cas ? Le segment de départ, c'est tout...
Dans l'autre sens, quand M se dirige vers B, AM augmente, donc ME aussi et le carré itou...
Quand M est sur B, AM=10 et le carré a 10 cm de côté...
Et le triangle, puisque ME augmente, il augmente de taille ?
Bin non parce que si AM augmente, le côté ME augmente aussi, oui, mais alors c'est BM qui diminue...
Quand est M sur B, AM= 10 donc ME = 10 et BM=0...
Le côté [BM] n'existe plus, il est réduit au point B...
A quoi ressemble alors le dessin ?
Un carré ABCD de 10 cm de côté... et dans le prolongement du côté [BC] (ou [MC] comme on veut il y a un segment de longueur BE (ou ME comme on veut puisque B et M c'est le même point maintenant)...
Résumé : on voit un carré ABCD (ou AMCD comme on veut) de 10 cm de côté et en dessous du carré, et précisément en_dessous du côté [BC], un segment de 10 cm de longueur...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#11 22-09-2018 12:18:38
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 992
Re : Problème géométrique de 2nde
Re,
Bon alors, j'en termine...
Demander des explications si nécessaire...
2.A) [tex]0\leqslant x \leqslant 10[/tex] ou [tex]x \in |0\,;\,10][/tex]
2.B) [tex]f(x)= x^2[/tex] et [tex]g(x)=\dfrac{x(10-x)}{2}=\dfrac{10x-x^2}{2}[/tex]
2.C) [tex] f(x)[/tex] --> courbe1, [tex]g(x)[/tex] --> courbe2
2.D) le $x$ solution est tel que [tex]$3<x<4$[/tex]
2.E) On demande de résoudre l'équation [tex] f(x)=g(x)[/tex]
Donc on cherche $x$ tel que [tex] f(x)=g(x)[/tex]
Ce qui nous donne l'équation : [tex]x^2=\dfrac{10x-x^2}{2}[/tex]
On multiplie le deux membres par 2 :
[tex]2x^2 =10x-x^2[/tex]
On arrive à
[tex]3x^2-10x =0[/tex]
Ou encore :
[tex]x(3x-10) =0[/tex]
On sait depuis la 3e qu'on a deux solutions $x=0$ et $x=\frac{3}{10}$...
Interprétation
Résoudre l'équation [tex] f(x)=g(x)[/tex], c'est chercher pour quelle valeur de $x$, donc de la longueur AM, on a :
Aire du carré = Aire du triangle
$x=0$ est une solution de l'équation, pas une réponse à la question : en effet pour $x=0$, l'aire du carré et celle du triangle sont nummes.
Il n'y a plus ni carré, ni triangle...
Donc réponse :
si $AM =\frac{10}{3}\;cm$ alors les deux aires sont égales...
Vérification :
Aire du carré = [tex]\left(\frac{10}{3}\right)^2=\frac{100}{9}\;cm^2[/tex]
Aire du triangle = [tex]\dfrac{\frac{100}{3} -\frac{100}{9}}{2}= \dfrac{\frac{300}{9} -\frac{100}{9}}{2}= \dfrac{\frac{200}{9}}{2}=\dfrac{100}{9}\;cm^2[/tex]
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
Pages : 1
Discussion fermée









