Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
Pages : 1
Discussion fermée
#1 18-01-2018 12:39:42
- saga974
- Membre
- Inscription : 17-01-2018
- Messages : 8
Calcul Aire integrale
Bonjour à TOUS,
Voici mon problème pour le calcul d'une aire d'integrale.
Pour moi ma réponse serait -4 mais visiblement ce n'est pas cela
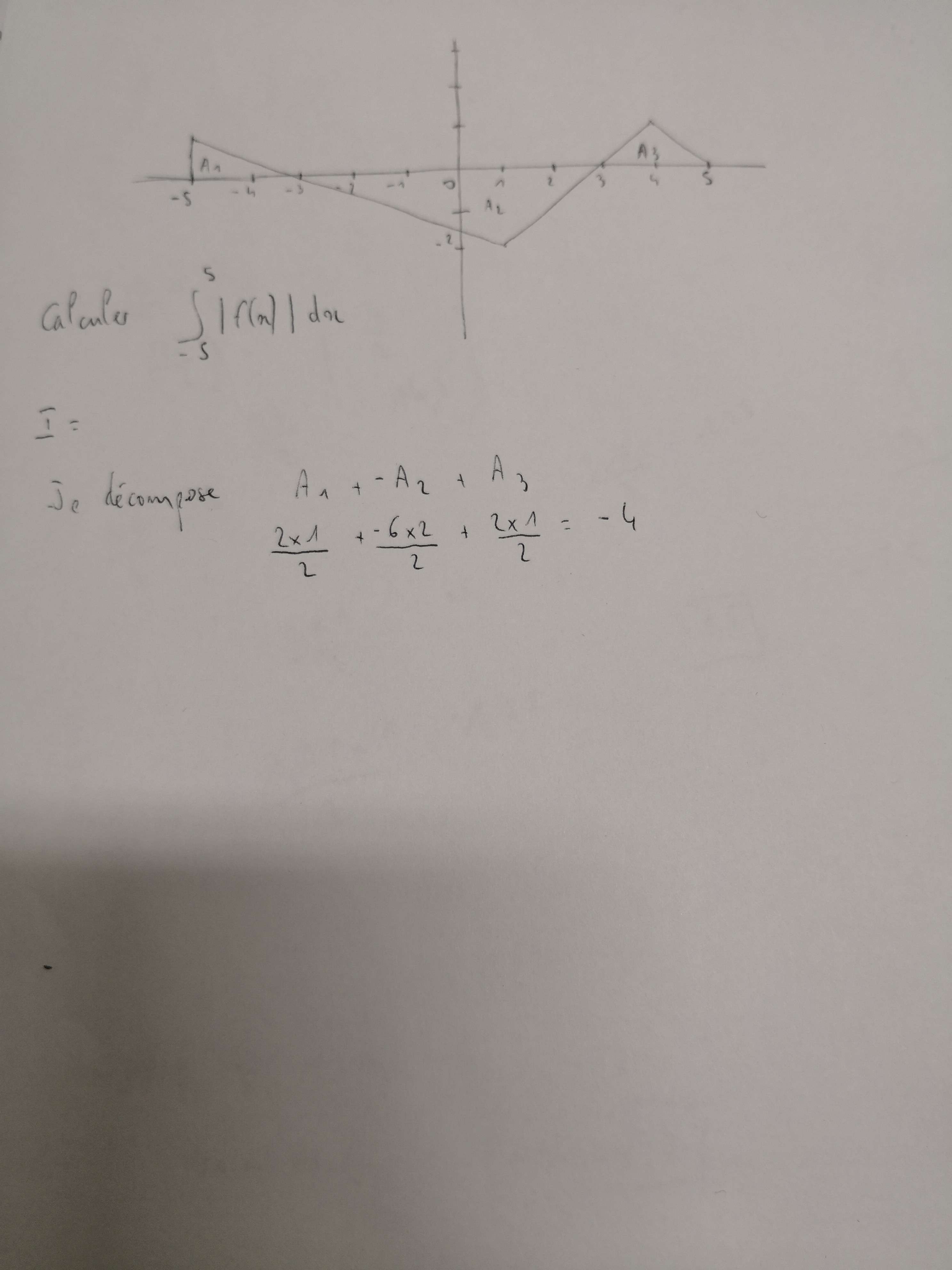
Merci d'avance pour votre soutien
Hors ligne
#2 18-01-2018 12:52:08
- Yassine
- Membre
- Inscription : 09-04-2013
- Messages : 1 090
Re : Calcul Aire integrale
Bonjour,
Tu y es presque !
Ton calcul correspond à $\displaystyle \int_{-5}^{5} f(x)dx$ alors qu'on te demande $\displaystyle \int_{-5}^{5} |f(x)|dx$
Il ne faut pas oublier le signe "valeur absolue" dans l'intégrale !
L'ennui dans ce monde c'est que les idiots sont sûrs d'eux et les gens sensés pleins de doutes. B. Russel
Hors ligne
#3 18-01-2018 14:08:46
- saga974
- Membre
- Inscription : 17-01-2018
- Messages : 8
Re : Calcul Aire integrale
Merci Yassine de ton éclaircissement mais valeur absolue ça ne me parle pas du tout.
Quel calcul dois je faire ?
Hors ligne
#4 18-01-2018 15:09:41
- Yassine
- Membre
- Inscription : 09-04-2013
- Messages : 1 090
Re : Calcul Aire integrale
La valeur absolue d'un nombre, c'est soit le nombre lui-même s'il est positif ou nul, soit son inverse s'il est négatif. C'est donc une grandeur toujours positive ou nulle. Exemple $|+3|=+3$ et $|-3|=+3$.
Dans ton exemple, $f(x)$ est positive si $-5\le x \le -3$ ou $3\le x \le 5$ et et négative si $-3 < x < 3$
Donc, la fonction $|f(x)|$ coïncidera avec $f(x)$ sur $[-5,-3] \cup [3,5]$ et sera égale à $-f(x)$ sur $]-3,3[$.
Ce qui revient à garder le graphe identique à gauche de $-3$ et à droite de $3$ et à prendre son symétrique par rapport à l'axe des $x$ entre $-3$ et $3$ et calculer l'aire avec ce nouveau graphe. Tu devrais trouver $8$
L'ennui dans ce monde c'est que les idiots sont sûrs d'eux et les gens sensés pleins de doutes. B. Russel
Hors ligne
#5 18-01-2018 16:16:14
- saga974
- Membre
- Inscription : 17-01-2018
- Messages : 8
Re : Calcul Aire integrale
Ton explication est clean je comprends mieux l'histoire des absolues. Ça revient à dire en gros qu'une valeur bien qu'elle soit négative sera toujours positive au final
Hors ligne
#6 18-01-2018 16:22:22
- Yassine
- Membre
- Inscription : 09-04-2013
- Messages : 1 090
Re : Calcul Aire integrale
En gros oui, mais attention à la formulation : Plutôt que de dire "qu'une valeur bien qu'elle soit négative sera toujours positive au final", on dira plutôt "que la valeur absolue d'une valeur, bien que la valeur soit négative, sera toujours positive au final".
L'ennui dans ce monde c'est que les idiots sont sûrs d'eux et les gens sensés pleins de doutes. B. Russel
Hors ligne
Pages : 1
Discussion fermée








