Forum de mathématiques - Bibm@th.net

Re,

Je penche pour un "oui", mais essaie d'expliquer - montrer - concrètement l'intérêt du TVI dans le cas du pendule de Foucault : conçu pour matérialiser la rotation de la Terre, il remplit son office, alors à quelle finalité destines-tu ici l'utilisation dudit TVI ?

Voilà pour moi (mais d'autres avis seraient les bienvenus !) ce que tu devrais expliciter...

@+

Bonjour Brigitte,

As-tu eu l'impression d'écrire une réponse à la question précise de tilda ?
Moi, non !
Alors pourquoi  avoir utilisé le cadre Réponse rapide ou avoir cliqué sur la mention Répondre sous le dernier post présent ?
Parce que dans les deux cas, tu as fait usage du verbe Répondre ?

Toi, oui ?
Alors, c'est peut-être grave, il faut consulter rapidement un... dictionnaire en ligne ^_^.

Ce n'est pas parce qu'une Recherche Google fournit un lien direct vers cette discussion qu'il faut s'arrêter de penser !

Tu vas donc d'urgence cliquer sur ce lien  Nouvelle discussion, (tu le trouvais en arrivant ici
donner un titre à ton problème,
copier/coller ton sujet dans la fenêtre cadre qui s'est ouverte que je laisse ouverte à cet effet.

Ne perds pas de temps, je supprimerai ton message dans les 36 h et tu n'auras pas de réponse d'ici là.
Tant qu'elle est présente ici, ta question introduit un "bruit de fond" dans la discussion en cours et gênera aussi bien tilda que toi.
La discussion que tu vas ouvrir bénéficiera des mêmes conditions que la présente : tu as ainsi l'assurance que n'y sera pas accepté tout message parasite...

Merci de ta compréhension,

Cordialement,

       Yoshi
- Modérateur -

Bonjour,

Merci Pidelta...

@medouard770
Pidelta a raison, si tu es en manque de forums pour poster, dis-le, je peux t'en fournir au moins 4 ou 5...
Cela dit, ce procédé s'apparente à
- de l'abus de confiance
- une tentative de recrutements d'esclaves consentants.

Certains tolèrent  cette façon d'agir, nous, non !

En conséquence, je ferme la discussion.

       Yoshi
- Modérateur -

[EDIT] Et suite au message insultant déposé (sous forme de signalement) en réponse à mes remarques, toujours dans mon rôle, j'ai banni medouard770...

Re,

Wow !
Ton lien est une vraie mine de diamant...

@+

Bonjour,

@Borassus : "Distance algébrique" ? Tu veux dire "Mesure algébrique" ? Sinon, je ne sais pas ce que c'est...
Si oui :
notée $\overline{AB}$,  la "mesure algébrique du segment [AB]" était telle que :
$\overline{AB}=-\overline{BA}$,
s'y appliquait la relation de Chasles : $\overline{AB}+\overline{BC}= \overline{AC}$ pour autant que A, B et C soient sur la même droite, munie d'un repère normé.
on avait alors $\overline{AB}=x_B-x_A$
Où, si (O,I) était ledit repère normé, $x_B=\overline{OB}\,\text{ et }x_A= \overline{OA}$
Voilà plus de 30 ans (probablement plus de 40 !) que cette notion est restée enfouie dans la naphtaline... alors je reste prudent, je risque d'oublier une "bricole" !
Elle était encore utilisée en 1966, année où j'ai passé mon Bac Mathématiques Élémentaires...
Je ne me souviens pas quand elle a été abandonnée...
Peut-être bien cette année-là ce fut la cause de l'apparition dans les programmes de l'obligation pour utiliser la réciproque du théorème de Thalès, de mentionner la clause que les points A, B et C d'une part et A, B' et C' étaient placés dans le même ordre sur les droites (AC) et (AC') pour pouvoir affirmer l'égalité des rapports $\dfrac{AB}{AC}$ et $\dfrac{AB'}{AC'}$ (après leurs calculs séparés) et conclure au parallélisme des droites (BB') et (CC'). Je n'ai pas de certitude : les voies des membres de la Direction des Programmes m'ont toujours parues impénétrables...
Mais certes, cela ne dit pas pourquoi la notion a disparu...
Parente pauvre des vecteurs ?
Obligation mal comprise (souvent sous-entendue ?) de définir un repère normé sur la droite où on l'utilisait ?

Amha, tu pers ton temps à chercher pourquoi... On ne pourra faire que des supputations !

@+

Bonjour,

Et alors ?
Oui, mais pas plus que ça. Je leur avais montré comment avec n impair >1, tout triangle de côtés $n,\,\frac {n^2-1}{2},\,\frac {n^2+1}{2}$ était un triangle rectangle... en vérifiant par calcul littéral que la réciproque du théorème de Pythagore s'appliquait bien.
je doute qu'ils s'en fussent souvenus

Mais non, je n'en avais pas "fait" un théorème : je l'avais montré à titre de "curiosité".
Sinon aurais-je dû accepter que, tombant un jour sur un triangle $\{4,2 ; 5,6 ;7\}$, ils ressortent :
Je sais que le triangle 3;4;5 est connu depuis la Haute Antiquité pour être un triangle rectangle.
Or, il se trouve que ce triangle 4,2 ; 5,6 ;7 est tel que 4,2 = 3 x 1,4 ; 5,6 = 4 x 1,4  et 7 = 5 x 1,4.
Ce triangle, dont les côtés sont multiples de 3-4-5, est donc bien un triangle rectangle...

Avec le risque, que plus, tard, sabotant plus ou moins leur justification, un grincheux ou un puriste extrême,  leur refuse la réponse.

Bin, oui, d'habitude si prompt à ne pas faire comme les autres, il m'arrivait d'être prudent, voire "rétrograde"...

La 1ere question de l'exercice de construction en avait dérangé beaucoup (je m'y attendais) : cette demande était bien trop inhabituelle pour eux.
Moi, dès sa découverte, je l'avais trouvé particulièrement révélateur et j'avais décidé qu'il ferait partie de ma panoplie d'exercices...

@+

Re,

Le fait est que ce qui ressemble à de la Géométrie ne commence vraiment qu'en 4e, il ne faut pas perdre de vue que ma génération en mangeait sérieusement dès la 6e et que tout le monde n'entrait pas en 6e...
Je suis contre les Groupes de niveau, j'ai vu ce que ça avait donné sur une classe entière de 3e : il ne faut pas les prendre pour des aveugles, ils avaient été tout à fait capables de comparer leur niveau avec les autres classes : << Pourquoi on travaillerait ? On sait bien qu'on est les cons du Collège ! >> (sic). De plus, de vrais groupes de niveau ne peuvent coexister 1 année entière dans la même salle, et 2 profs : Où va-t-on les trouver (les salles libres et les profs ?).
J'ai fait ça - une fois durant un trimestre - contraint et forcé, suite à une erreur de jugement de ma part sur le contenu et le timing d'une interro en 3e, où  sur 29 élèves j'avais 1 fois 19 et 1 fois 20, une petite partie (7 ou 8... c'est loi, hein...) entre 10 et 14, le reste entre 0 et 8...
J'avais bien dû assumer mon erreur, la reconnaître devant les intéressés et faire bosser les deux têtes (2 filles, au passage !) et avancer avec elles en même temps (comme dirait quelqu'un ;-D) que je redémarrais de 0 avec les autres... il avait fallu reprendre assez vite (sans trop) avec les uns et avancer le programme (pas trop vite et en ponctuant de quelques exercices d'approfondissement avec les 2 têtes) pour pouvoir raccrocher les wagons...
Bien sûr, tous étaient dans la même salle.
J'avais eu la chance de voir, dans le passé, fonctionner une classe unique allant de la Section enfantine au CM2 et aussi - durant une semaine de m'y coller : c'était de la haute voltige, l’œil rivé sur le chronomètre pour bien gérer les décrochages des changement de niveau...
Je ne crois pas que je me serais lancé en 3e sans cette petite expérience et je me serais retrouvé dans la mélasse.
Bah... c'est du passé n'en parlons plus (comme dit la chanson) !

Autre problème  face aux théorèmes, définitions propriétés et autre réciproques, devant un exercice beaucoup, ressemblent à "des poules trouvant un couteau".
Beaucoup ne sont jamais entendu expliquer à quoi servait tout ça...
J'en avais fini par leur donner à l'impromptu des interros de leçon hors norme...
Exemple :
Je donnais deux cercles (hypothèses /conclusion) l'un à côté de l'autre, centre marqué, un diamètre tracé et un point sur les cercles.
Plus, dessin de droite, j'ajoutais un angle droit....
Je demandais simplement qu'on me donne l'énoncé du théorème correspondant et je demandais qu'on mette une barre verticale dans le texte à l'endroit où se terminaient les hypothèses (ou encore les données) et où donc commençait la conclusion...
Je leur précisais le pourquoi du procédé : savoir sa leçon ce n'est pas la réciter comme un perroquet, les perroquets n'ayant rien à faire en classe.

Certains (pas tous, pas ceux capables d'écrire : la nature du quadrilatère ABCD est un triangle... sic), finissaient par comprendre ce que Borassus a dit plus haut : ouvrir les yeux, repérer les figures élémentaires des théorèmes, définitions etc vus en cours. Et que c'est par là que tout commence... Ce n'était pas aussi évident que cela peut en avoir l'air!
C'est pourquoi le dessin (pourtant fourni) n'est pas aisé à décrypter pour un 3e lambda : beaucoup de traits et de points, deux cercles sécants... Beaucoup ne remarquaient même pas que le titre de l'exercice constituait une piste...

Autres exercices en 4e (en DM) déstabilisants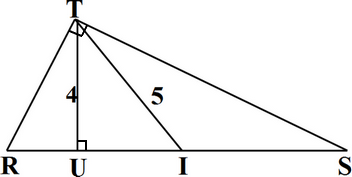

1. Construire en vraie grandeur le triangle rectangle RTS ci-dessus, en justifiant chaque étape de la construction, sachant que H est le pied de la hauteur relative au côté [RS] et I le milieu de celui-ci,TU = 4 cm et TI = 5 cm.
2. Calculer ensuite UI, RU, RT et TS (pour les deux dernières, donner les résultats arrondis à à 0,1 cm près.)

Et :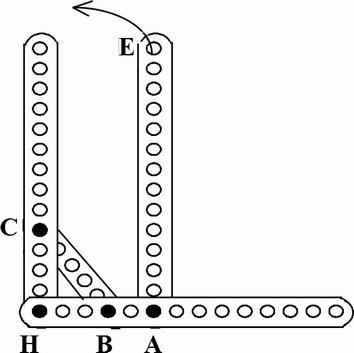

Trois barres de meccano ont été assemblées de façon rigide et une quatrième est mobile  : les points noirs représentent les écrous de fixation.
Les 3 grandes barres comportent 14 trous, la petite barre en comporte 6. On va faire pivoter la grande barre mobile. Tous les trous sont régulièrement espacés.
1. Que pouvez-vous dire du montage des 3 barres fixes ?
2. En face de quel trou de la barre fixe  [HC] le dernier trou E de cette barre mobile [AE] va-t-il venir se fixer ? (Réponse attendue : un n°)

Beaucoup ne voyaient pas le pourquoi de la question 1, la plupart des autres n'y auraient pas pensé tout seuls. De plus il y avait une vacherie finale...

Ces exos venaient en DM après la leçon sur Pythagore...

@+

Re,

Justification intéressante !
Moi, j'introduisais la notion de vitesse limite d'exécution des calculs propre à chaque individu.
Je disais : la différence entre le Prof et vous, c'est qu'il connaît sa vitesse limite et qu'il travaille en étant en dessous : les erreurs arrivent aussi chez lui s'il la dépasse... Donc, tâchez de la connaître pour vous, afin de travailler un peu moins vite...
Ils ne savent pas non plus, en général,apprendre à apprendre ! A aussi, c'est occulté tout au long de la scolarité

Tiens, un exo d'un de mes DM de 3e qui n'avait pas plu du tout... ;-)
J'espère qu'il t'agréera...

En 6e, sur un un papier quadrillé, à partir des pentes (sans prononcer le mot) des droites qui s'appuient (passent par) sur les points d'intersection des marches et des contre-marches, approchées en disant pour aller de A à B (deux de ces points) je monte (ou descend) verticalement de combien de carreaux puis je me déplace horizontalement (vers la G ou la D) de combien de carreaux ?
En 3e, on arrivait à la tangente, au coefficient directeur...

Je te ferai un peu plus tard un dessin...

@+

Re,

Bin, si c'est d'un niveau assez relevé pour toi (les autres, je ne sais pas), moi en tout cas, je ne risque pas de m'auto-épater ;-)
(Très) Difficile d'être et avoir été...Je commence à me rouiller sérieusement !

Je ne sais plus quel cynique a dit :
Les vieillards aiment à donner de bons conseils pour se consoler de ne plus être en mesure de donner de mauvais exemples !

Pourquoi demander la permission ?
Membre à part entière, pourquoi devrait-on restreindre ton champ de publication ?...
Je ne vois pas où il pourrait y avoir contre-indication ou violation de notre charte dans ta proposition...

@+

Ouf !
En principe, ça colle...
Qu'en sera-t-il demain ? Et en octobre prochain ?

@+

Re,

Raaaah, c'est rageant !

Réglage sur (UTC + 01h 00) Europe centrale, Afrique de l'Ouest. Je n'ai pas touché au reste : rien de coché...
Je fonctionne avec Windows 7 et Firefox...
L'heure affichée par ma ma machine est 21:49
Heure Bibmath : 1 h de moins

Affaire à suivre...
@+

[EDIT]
Je viens de demander à windows de mettre là jour  l'heure sur time.nist.gov. Cela va-t-il durer ?

[EDIT 2] Ma machine est à l'heure, pas Bibmath... Diable !

Bonsoir,

Je rejoins vam sur les segments...
Mais, je pense qu'à l'époque en 6e, on savait déjà que la différence de deux nombres a et b (a>b), c'est le nombre c qu'il faut ajouter à b pour trouver a
Comme a et b sont aussi des lettres, si elles te gênent :
- garde seulement différence de deux nombres et oublie le "a et b" qui suit
- remplace (a> b) par (premier nombre supérieur au second)
Dans ce cas  : x+1,5+2,1 = 4 devenant : ? + 3,6 = 4 on est confronté au choix
- à une soustraction  : 4 - 3,6 = ?
- à une addition à trous (ainsi que dit par vam) ce qui nous ramène à l'item précédent...

D'ailleurs en 5e, après avoir vu comment additionner deux relatifs, on passait à la soustraction.
Et soit on balançait la règle, soit (et c'était mon cas) on montrait comment y accéder en usant de la définition donnée plus haut (sans se préoccuper du a>b évidemment)
Par exemple:
(-5) - (+3) = ? est remplacée par une devinette dont on fait trouver la réponse via un petit raisonnement :
On se demandait donc s'il était possible de répondre à : (-5) + ? = (-3)
Il est simple de voir que
- derrière ? il n'y a pas un nombre négatif (règle de l'addition)
- si le nombre n'est pas négatif, c'est qu'il est positif :
  * la règle d'addition nous permet de dire que le nombre cherché est inférieur à 5
  * la conséquence est donc que que ? c'est +2
On arrive alors à (-5)+(+2)= (-3) soit en revenant à la soustraction (-5)-(-3)= (-5)+(+3)= (+2)
On étudie ensuite les 3 cas  restants pour en arriver à la formulation :

Pour soustraire deux nombres relatifs, il faut ajouter au premier l'opposé du 2nd et on a bien vu ainsi que la définition de la définition donnée de la différence de deux nombres a et b donnée plus haut s'applique encore (et que sa formulation n'en est pas très éloignée).

@+