Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Un mini-jeu » 11-12-2020 21:39:34
Aucune idée.
#2 Enigmes, casse-têtes, curiosités et autres bizarreries » Un mini-jeu » 11-12-2020 02:24:47
- tibo
- Réponses : 5
Bonjour,
Au cours de mes activités vidéoludiques, je rencontre régulièrement le mini-jeu suivant :
Le plateau de jeu est constitué d'un carré de $n\times n$ cases. Chaque case est soit allumée, soit éteinte.
On peut cliquer sur chaque case afin de changer l'état de la case et les cases adjacentes (pas en diagonale).
Le plateau de départ est dans un certain état (quelques cases éteintes et d'autres allumées), et il faut réussir à toutes les allumer.
Rencontrant ce mini-jeu régulièrement, je commence à être un peu lassé de réfléchir à chaque fois sur un cas particulier, alors qu'il doit probablement exister une méthode plus générale.
Je sais que des solveurs existent sur le web, mais c'est pas drôle.
Faire un solveur maison est bien plus intéressant, et l'aspect purement théorique de la chose doit être sympa à étudier.
Je vous partage donc ma récente lubie pour y réfléchir à plusieurs si cela vous tente.
Je vous laisse là dessus pour l'instant pour ne pas se focaliser sur mes pistes de recherche alors qu'il en existe peut-être de meilleures.
#3 Re : Programmation » Python » 17-11-2020 17:30:09
Bonjour,
Qu'à tu essayé de faire ?
As-tu commencé à écrire un programme, mais il ne fonctionne pas ?
Si tu ne sais pas du tout par où commencer, il va falloir faire un peu de math :
Quels critères connais-tu pour déterminer si un quadrilatère est un parallélogramme ?
#4 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Combien de cotés » 29-10-2020 12:39:20
Salut,
Je suis assez embêté par ta question ...
Elle pose surtout la question de la définition d'un "côté".
Pour être sûr, j'ai cherché un peu sur internet :
L'article Wikipédia utilise comme unique source le site Scilab et donne comme définition :
Chacun des éléments qui forment la frontière d’une figure géométrique plane.
Et je ne suis pas plus avancé parce c'est quoi un élément... ?
Mon avis est que la notion de côté n'a de sens que pour les polygones.
Donc selon moi ta question n'a pas de réponse.
#5 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » grille 3 par 3 » 20-10-2020 09:27:33
Salut,
@Yoshi : J'ai l'impression que tu ajoutes des règles pour obtenir absolument un carré parfait. Mais nul part il n'en est fait mention dans l'énoncé.
1, 23, 2577 sont bien 3 entiers, non ? Alors j'ai parfaitement le droit de les utiliser...
Parfaitement, l'énoncé t'autorise à le faire.
Par contre, la notion de "case paire" est certes peu claire.
Je pense que "case paire" signifie "case contenant un nombre pair".
J'ai compté 0, 4 ou 6 cases contenant un nombre pair.
@48PierrelePetit : On a compris l'énoncé de la même façon.
Néanmoins, il te manque pas mal de configurations.
#6 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » grille 3 par 3 » 19-10-2020 09:22:37
Salut,
#7 Re : Entraide (collège-lycée) » Aide à l'étude des fonction contenu » 11-10-2020 23:25:43
Salut,
Des fonction contenu ?
Peut-être veux tu plutôt parler de fonctions continues ?
Difficile de te faire un cours complet sur cette notion.
On ne ferait probablement que réécrire ce qu'il y a dans ton livre ou ton cahier.
Mais si tu as des questions plus ciblées, n'hésite pas.
Qu'as tu compris sur ce chapitre ? Il y a forcément des choses que tu as comprises.
Et que penses-tu ne pas avoir compris ?
#8 Re : Entraide (collège-lycée) » suite arithmetique » 11-10-2020 23:20:34
Salut,
Aide toi, et Bibmath t'aidera.
Qu'as-tu fais dans cet exercice ?
#9 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Deux pièces de monnaie » 10-10-2020 21:02:33
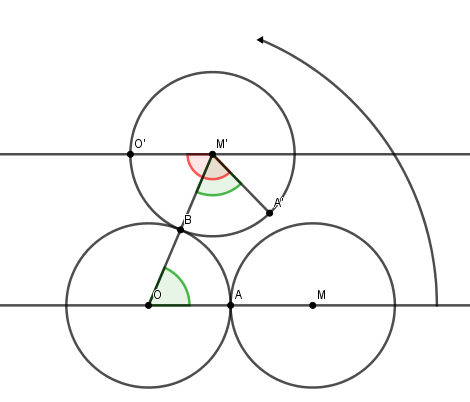
Le cercle de centre $O$ est la pièce immobile, celui de centre $M$ est la pièce qui va tourner.
Le morceau de scotch est placé en $A$, point de contact des deux cercles à l'état initial.
Maintenant, même problème mais avec des pièces de taille différentes !
PS : Cette énigme aurait sa place dans la section "Problème de géométrie" du forum.
Mine de rien, il fait quand même appel à un peu de trigo, et je ne m'attendais pas à devoir utiliser les angles alternes-internes.
#10 Re : Entraide (collège-lycée) » GeoGebra - limites » 05-10-2020 18:36:04
Salut,
Bah je découvre que GeoGebra sait calculer des limites...
Pour ton problème, il faut remplacer les 'n' par des 'x'.
Par défaut, x est une variable pour GeoGebra, alors que n est une constante.
#11 Re : Entraide (collège-lycée) » Dénombrements et combinatoires » 04-10-2020 14:17:05
Bonjour,
Te faire le corrigé, non, tu ne trouveras pas ça ici.
Par contre si tu nous dis ce que tu as fait, on peut te dire si c'est juste.
#12 Re : Entraide (collège-lycée) » démonstration par récurrence » 03-10-2020 18:18:52
Re,
J'ai supposé aussi que la forme exponentielle n'avait pas encore été vue, parce que dans le cas contraire, la récurrence est totalement inutile.
#13 Re : Entraide (collège-lycée) » démonstration par récurrence » 03-10-2020 15:11:08
Salut,
Les formules trigo d'additions ont effectivement disparues du programme de première.
Et pas évident de faire sans ici.
Peut-être qu'on peut passer par un point de vue plus géométrique :
Un nombre complexe est entièrement défini par son module et son argument.
Et on a les propriétés suivantes :
- Le module d'un produit est le produit des modules ;
- L'argument d'un produit est la somme des arguments.
#14 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Casse-têtes » 29-09-2020 17:25:21
Salut,
Commençons par pinailler un peu :
Le chiffre 34 pourrait-il être la solution.
Tu voulais dire le "nombre 34" ?
#15 Re : Entraide (collège-lycée) » Racine carrée d'un nombre complexe » 27-09-2020 12:25:52
Salut,
La question 3a. commence par te demander de trouver une solution de l'équation dans le cas b>0.
Pour en trouver une autre, aide toi de la question 1) :
Si $z$ est une solution, alors $-z$ en est aussi une...
#16 Re : Le coin des beaux problèmes de Géométrie » Géométrie d'une came » 27-09-2020 00:09:29
Bonjour,
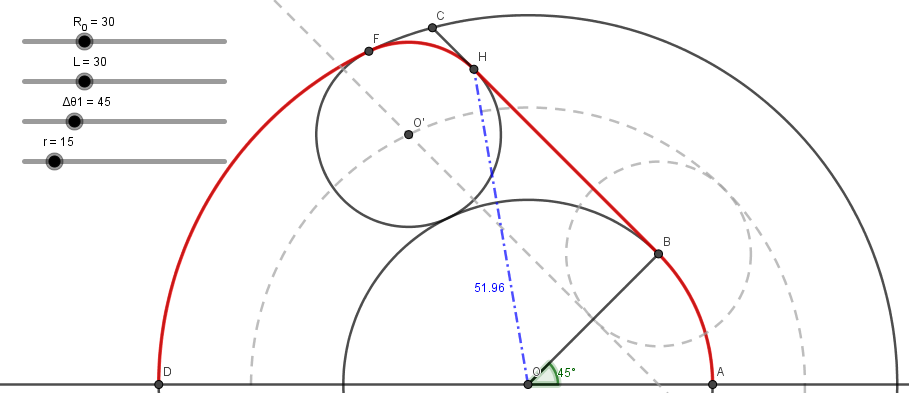
En essayant de reconstruire la figure à mon tour, j'ai eu un autre problème de taille.
Si j'ai bien compris, le triangle OBC est rectangle en B.
Donc en théorie $OC^2=R_0^2+BC^2$.
Sauf que $OC^2=60^2=3 600$
Et $R_0^2+BC^2=30^2+52^2=3604$...
PS : d'ailleurs, il n'y a pas un problème sur l'heure du forum ?
Parce qu'il est 1h30 du matin chez moi (et je suis bien en France).
#17 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Les mots " CHIODI" et "CLOUS" » 25-09-2020 18:40:34
Salut,
#18 Re : Entraide (collège-lycée) » nombres - valeur absolue » 25-09-2020 18:18:17
Salut,
Pour info à ceux qui ont répondu à Tania, la valeur absolue est désormais introduite en seconde comme la distance entre deux réels.
On voit aussi comment écrire un intervalle à l'aide de la valeur absolue : $x\in[a-d,a+d]\Leftrightarrow |x-a|\le d$.
Mais on reste sur une conception très géométrique de la valeur absolue.
Ses propriétés analytiques ne sont abordées qu'en première, notamment sa définition en tant que fonction et les résolutions d'équations.
D'où les questions que se pose Tania je pense.
#19 Re : Entraide (supérieur) » Fonctions usuelles » 23-09-2020 21:08:39
Bonjour,
Qu'as-tu essayé de faire ?
L'énoncé te fourni déjà beaucoup d'aide :
- La fonction racine carrée est définie sur $\mathbb{R}_+$,
donc ce qui est sous la racine doit être positif,
il faut donc résoudre l'inéquation $1-x^2\ge 0$.
- La fonction $ln$ est définie sur $\mathbb{R}^*_+$,
donc ce qui est dans le $ln$ doit être strictement positif,
il faut donc résoudre l'inéquation $x+\sqrt{1-x^2}>0$.
À toi de jouer !
#20 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » Problème d'addition » 18-09-2020 00:33:28
Salut,
Je vais jouer mon pinailleur
Et oui, mon message n'a pas vraiment plus d'utilité que ça.
Face à ce genre d' "énigme", j'ai toujours envie de créer une fonction ad hoc $+ : \mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}$ en prenant des images au pif.
Et me demander pourquoi ma fonction serait moins "logique" que la fonction imaginée par le concepteur de l'énigme.
Sinon ça va vous ? ^^
#21 Re : Entraide (supérieur) » Proba conditionnelle - Deux stations météos » 11-12-2019 16:59:12
L'exercice classique que je donne à mes premières est le suivant :
"Une maladie touche une partie de la population.
Pour la dépister, il existe un test fiable à 95% : c'est-à-dire que si l'on est malade, le test est positif dans 95% des cas, et si l'on est sain, le test est négatif dans 95% des cas.
Je viens de faire le test, et il est positif. Quelle est la probabilité que je sois malade ?"
Posé ainsi, ce problème ne peut pas être résolu.
J'ai besoin de connaître la probabilité a priori que je suis malade.
En général, l'énoncé donne également la proportion de la population touchée par la maladie, et on l'utilise comme proba a priori.
Mais il existe des variantes où l'on considère d'autres paramètres (génétiques, environnementales,...) qui modifient la probabilité a priori.
Pour revenir au problème initial, il est facile de le transposer dans le contexte épidémiologique :
"Une maladie touche 1/3 de la population.
Il existe deux tests A et B pour la dépister, respectivement fiable à 95% et 90% (au sens défini plus haut).
J'ai passé les deux tests. Le A est positif et le B est négatif. Quelle est la probabilité que je sois atteint par cette maladie ?"
Et l'étude des cas extrêmes est peut-être plus réaliste. (Il est vrai que l’existence de stations météo dans un pays où il ne pleut jamais est étrange.)
On peut imaginer que cette maladie ne touche que les femmes et que je suis un homme.
Rien ne m'empêche de passer quand même les tests, et que l'un des tests soit positif.
La probabilité que je suis malade reste nulle.
#22 Re : Entraide (supérieur) » Proba conditionnelle - Deux stations météos » 10-12-2019 18:42:14
Salut,
Je rejoins verdurin.
La probabilité qu'il pleut demain a priori est essentielle.
On peut le voir sur le cas extrême d'un pays où il ne pleut jamais : $P(M)=0$.
Dans ce cas, quelque soit la prédiction des stations météo, la probabilité qu'il pleuve reste à 0.
Et effectivement, l'indépendance des stations semble assez naturelle.
Merci verdurin pour les calculs ; je l'avais fait sur feuille, et j'ai trouvé la même chose, mais j'avais dû mal à trouver la motivation de l'écrire ici.
#23 Re : Entraide (supérieur) » Proba conditionnelle - Deux stations météos » 06-12-2019 00:41:47
ha oui... comme ça, ça marche bien.
Sauf que de ce que j'en sais l'énoncé ne précisait pas une telle indépendance.
Je demanderais à ma collègue si elle peut me donner l'énoncé original
#24 Entraide (supérieur) » Proba conditionnelle - Deux stations météos » 05-12-2019 13:16:27
- tibo
- Réponses : 15
Salut,
Une collègue m'a posé un problème que sa fille a eu en Khôlle.
Et je dois avouer qu'il me pose quelques difficultés.
Je n'ai pas l'énoncé exact, mais le voilà en substance :
"On s'intéresse à la probabilité qu'il pleuve demain.
Des études statistiques ont montré qu'il pleut 1 jour sur 3.
Deux stations météos A et B tentent prédire cela plus précisément.
La station A est fiable à 95%, c'est-à-dire que s'il pleut demain, il y a 95% de chance qu'elle l'ait prédit ; et s'il ne pleut pas, il y a 95% de chance qu'elle l'ait prédit.
La station B est fiable à 90%.
Pour demain, la station A a prédit qu'il pleuvra, la station B non.
Quelle est la probabilité qu'il pleuve demain ?"
Ça ressemble beaucoup à un problème de proba conditionnelle très classique, mais le fait qu'il y ait 2 stations complique un peu la chose...
On considère les événements
$P$ : "Il pleuvra demain."
$A$ : "La station A prédit de la pluie."
$B$ : "La station B prédit de la pluie."
On a $p(P)=\dfrac{1}{3}$
$p_P(A)=0.95$ et $p_{\overline{P}}(\overline{A})=0.95$
$p_P(B)=0.9$ et $p_{\overline{P}}(\overline{B})=0.9$.
On cherche à calculer $p_{A\cap\overline{B}}(P)$.
Alors calculer $p_{A}(P)$ et $p_{\overline{B}}(P)$ c'est facile, mais $p_{A\cap\overline{B}}(P)$...
Un indice ?
#25 Re : Enigmes, casse-têtes, curiosités et autres bizarreries » sphère composée de triangles identiques » 17-04-2019 07:14:45
Salut,
Il existe à ma connaissance une seule façon de paver une sphère avec des triangles équilatéraux tous identiques : avec huit triangles dont les cotés mesure 1/4 de périmètre d'un grand cercle (et possédant 3 angles droits).