Projection orthogonale
Si $D$ est une droite du plan, on appelle projection orthogonale sur $D$ l'application qui à tout point $M$ du plan associe le point $M'$ tel que $$\left\{ \begin{array}{l} M'\in D\\ (MM')\perp D \end{array} \right.$$

Si $P$ est un plan de l'espace, on appelle projection orthogonale sur $P$ l'application qui à tout point $M$ du plan associe le point $M'$ tel que $$\left\{ \begin{array}{l} M'\in P\\ (MM')\perp P \end{array} \right.$$
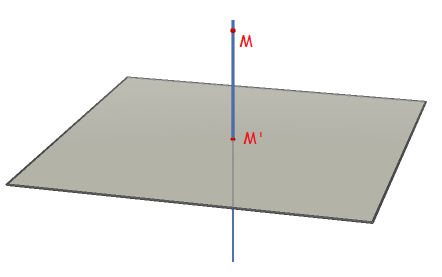
Si $D$ est une droite de l'espace, on appelle projection orthogonale sur $D$ l'application qui à tout point $M$ du plan associe le point $M'$ tel que $$\left\{ \begin{array}{l} M'\in D\\ (MM')\perp D \end{array} \right.$$ $M'$ est le point d'intersection de $D$ et du plan normal à $D$ passant par $M$.

Si on note $p$ cette projection, alors elle vérifie deux propriétés fondamentales suivantes :
- $\|x-p(x)\|=\inf_{y\in F}\|x-y\|$ : le projeté orthogonal minimise la distance de $x$ à $F$.
- Si $(e_1,\dots,e_p)$ une base orthonormale de $F$, on a $$p(x)=\sum_{i=1}^p \langle x,e_i\rangle e_i.$$
Dans un espace de Hilbert, on peut de la même façon définir la projection orthogonale sur un sous-espace fermé. Mais la propriété fondamentale pour pouvoir projeter est la convexité :

Remarques :
- Le théorème est formulé pour un espace de Hilbert réel. Il reste vrai pour un espace de Hilbert complexe, à condition d'ajouter une partie réelle dans la caractérisation : $$\forall z\in C,\ \Re e(\langle z-p(x),x-p(x)\rangle)\leq 0.$$
- Le théorème s'étend aux espaces préhilbertiens à condition de supposer que le convexe sur lequel on projette est complet.
- Si on ne travaille plus avec un espace de Hilbert, mais avec un espace de Banach, on peut perdre l'existence ou l'unicité d'un projeté sur un convexe fermé. Par exemple, si $E=\mathbb R^2$ muni de $\|\cdot\|_\infty$ et si $C=\bar B(0,1)$, alors $u=(2,0)$ est à distance $1$ de $C$, et pour tout $a\in [-1,1]$, $(1,a)\in C$ et $\|u-(1,a)\|_\infty=1$. Pour perdre l'existence, il faut se placer en dimension infinie. On peut considérer $E=\mathcal C([0,1])$ muni de $\|f\|=\|f\|_\infty+\|f\|_1$ et $C=\{f\in E:\ f(0)=1\}$. Alors, pour $g=1,$ la distance de $g$ à $F$ est égale à $1$, mais elle n'est pas atteinte.








