$$\newcommand{\mtn}{\mathbb{N}}\newcommand{\mtns}{\mathbb{N}^*}\newcommand{\mtz}{\mathbb{Z}}\newcommand{\mtr}{\mathbb{R}}\newcommand{\mtk}{\mathbb{K}}\newcommand{\mtq}{\mathbb{Q}}\newcommand{\mtc}{\mathbb{C}}\newcommand{\mch}{\mathcal{H}}\newcommand{\mcp}{\mathcal{P}}\newcommand{\mcb}{\mathcal{B}}\newcommand{\mcl}{\mathcal{L}}
\newcommand{\mcm}{\mathcal{M}}\newcommand{\mcc}{\mathcal{C}}
\newcommand{\mcmn}{\mathcal{M}}\newcommand{\mcmnr}{\mathcal{M}_n(\mtr)}
\newcommand{\mcmnk}{\mathcal{M}_n(\mtk)}\newcommand{\mcsn}{\mathcal{S}_n}
\newcommand{\mcs}{\mathcal{S}}\newcommand{\mcd}{\mathcal{D}}
\newcommand{\mcsns}{\mathcal{S}_n^{++}}\newcommand{\glnk}{GL_n(\mtk)}
\newcommand{\mnr}{\mathcal{M}_n(\mtr)}\DeclareMathOperator{\ch}{ch}
\DeclareMathOperator{\sh}{sh}\DeclareMathOperator{\th}{th}
\DeclareMathOperator{\vect}{vect}\DeclareMathOperator{\card}{card}
\DeclareMathOperator{\comat}{comat}\DeclareMathOperator{\imv}{Im}
\DeclareMathOperator{\rang}{rg}\DeclareMathOperator{\Fr}{Fr}
\DeclareMathOperator{\diam}{diam}\DeclareMathOperator{\supp}{supp}
\newcommand{\veps}{\varepsilon}\newcommand{\mcu}{\mathcal{U}}
\newcommand{\mcun}{\mcu_n}\newcommand{\dis}{\displaystyle}
\newcommand{\croouv}{[\![}\newcommand{\crofer}{]\!]}
\newcommand{\rab}{\mathcal{R}(a,b)}\newcommand{\pss}[2]{\langle #1,#2\rangle}
$$

 Bibm@th
Bibm@thCourbes fractales de Peano et de Hilbert
Il est bien connu, en géométrie, qu'un point est de dimension 0, et qu'une courbe, c'est de dimension 1, ça ne peut jamais remplir tout l'espace! Et bien, détrompez-vous! Le mathématicien italien Giuseppe Peano a construit en 1890 une courbe qui remplit tout le carré, sans jamais se recouper. Voyons comment faire : on partage un carré en 9 petits carrés égaux, et on exécute le dessin suivant :

Ce dessin sera le motif de base. Partageons maintenant toujours notre carré en 9, mais dans chaque petit carré, on trace le motif de base, que l'on peut tourner de sorte que l'on fasse un chemin continu. On obtient quelque chose comme :

Et on répète ainsi l'opération. La courbe ainsi obtenue à la limite (il n'y a pas de magie dans ce passage à la limite - on peut écrire une formule mathématique précise), est la courbe de Péano, qui remplit le carré : c'est une fractale, qui se caractérise notamment par son autosimilarité! Voyez sur l'applet ci-dessous comme il suffit de peu d'étapes pour aller au bout des possibilités de l'écran :
Plus généralement, une courbe qui est une surjection continue de [0,1]×[0,1] dans [0,1] est appelée courbe de Peano. Quelques années après Peano, en 1896, Hilbert en a donné une autre dont voici les premiers motifs :
 C'est Cantor le premier qui remarqua que l'intervalle [0,1] et le carré
[0,1]2 pouvait être mis en bijection. Peut de temps après, Netto démontra qu'une telle bijection ne
pouvait pas être continue. En particulier, la courbe de Peano, qui est continue et est surjective, ne peut pas être
injective.
C'est Cantor le premier qui remarqua que l'intervalle [0,1] et le carré
[0,1]2 pouvait être mis en bijection. Peut de temps après, Netto démontra qu'une telle bijection ne
pouvait pas être continue. En particulier, la courbe de Peano, qui est continue et est surjective, ne peut pas être
injective.
Consulter aussi...
Recherche alphabétique
Recherche thématique







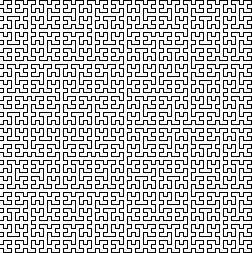
 C'est Cantor le premier qui remarqua que l'intervalle [0,1] et le carré
[0,1]2 pouvait être mis en bijection. Peut de temps après, Netto démontra qu'une telle bijection ne
pouvait pas être continue. En particulier, la courbe de Peano, qui est continue et est surjective, ne peut pas être
injective.
C'est Cantor le premier qui remarqua que l'intervalle [0,1] et le carré
[0,1]2 pouvait être mis en bijection. Peut de temps après, Netto démontra qu'une telle bijection ne
pouvait pas être continue. En particulier, la courbe de Peano, qui est continue et est surjective, ne peut pas être
injective.








