Triangle de Pascal
Le théorème suivant est connue sous le nom de relation de Pascal ($\binom n p$ désigne le nombre de parties à $p$ éléments dans un ensemble à $n$ éléments) :Théorème : Pour tous entiers $n$ et $p$ avec $1\leq p\leq n-1$, on a :
$$\binom np=\binom{n-1}p+\binom{n-1}{p-1}.$$
Supposons en effet que vous deviez former une équipe de foot (11 joueurs) parmi 22, et que parmi ces joueurs, il y a Zidane. Alors
vous avez deux choix :
- Soit vous faites une équipe avec Zidane : il vous reste 10=11-1 joueurs à choisir parmi 21=22-1.
- Soit vous faites une équipe sans Zidane : il vous reste 11 joueurs à choisir parmi 21=22-1!
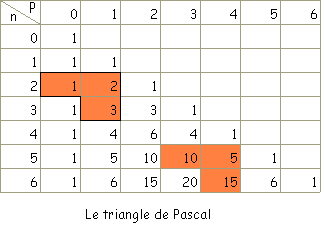
 Lorsque Pascal construit en 1654 son triangle arithmétique, il est loin d'être le premier à avoir organisé les nombres de cette façon. Le triangle arithmétique est même connu en Chine, en Inde ou dans les pays arabes dès le XIè ou le XIIè siècle. L'apport de Pascal est une étude systématique, et surtout pour réaliser cette étude, il utilise pour la première fois le raisonnement par récurrence.
Lorsque Pascal construit en 1654 son triangle arithmétique, il est loin d'être le premier à avoir organisé les nombres de cette façon. Le triangle arithmétique est même connu en Chine, en Inde ou dans les pays arabes dès le XIè ou le XIIè siècle. L'apport de Pascal est une étude systématique, et surtout pour réaliser cette étude, il utilise pour la première fois le raisonnement par récurrence.
Consulter aussi
Recherche alphabétique
Recherche thématique








